标签：
1-Linear Support Vector Machine
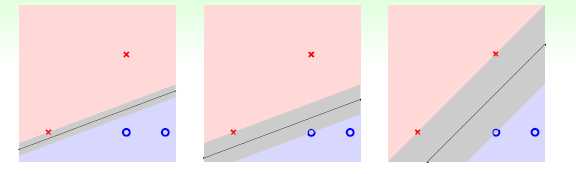
我们将这种定义为margin，则之前判断最优划分的问题转化为寻找最大margain的问题。
对于待选的几个w所表示的线，问题转化成利用对应w比较相对距离的问题。
此时定义w为方向向量，b为之前的w0，即bia。
由于w就是所求点到直线的法线方向，问题转化为求投影的问题。
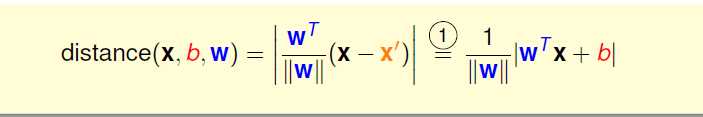
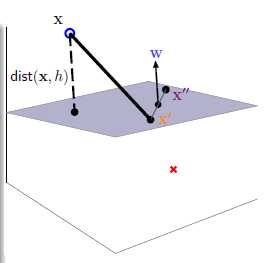
因为每个点对应符号yn只有在和距离表示的绝对值内部符号为+的时候才说明划分正确，所以可以乘上yn来去除abs()
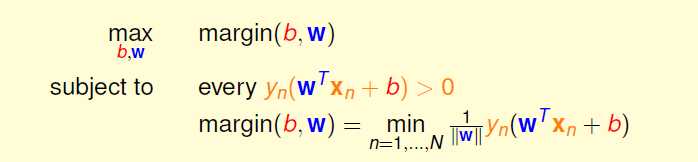
这里的距离是一种容忍度，所以我们选其中最近的那个。
因为我们是最主要的目的是选择b和w使得定性最短，所以我们可以把margin整体进行放缩，而不影响最值选取点。
这里，令后半部分乘积为1，则目标的最值讨论变为对1/||w|| 的讨论，问题得以简化。
然而，yn（xTxn+b) = 1 是一个很强的约束条件，这里将其放松为>=1。
这部分略过一些极值点可取的讨论。
这里又用了一个很tricky的常见技巧，把最大化问题转化为最小化其倒数的方法，然后去除根号，并为了后边的处理加上常数0.5：
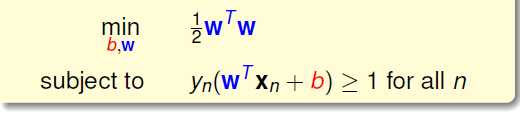
P.S. 1/sqrt(2)*[(1,1)T · (3,0) + (-1)] for EX.
有了这个选择的工具，我们引出SVM，即那些可以达到对应最值得点（向量），把它们定义为支持向量机。
luckily, 这是一个二次规划的问题，已经有了可行的求解工具，所以我们现在把它转化为标准形式，
左边是我们要求的，右边是标准形式：
另外的一些情况：比如遇到非线性问题，可以先利用映射转化为线性，另外上边讨论的为所谓hard-margin，是完全可分的线。
zn = (xn)—remember? :-) Z空间的转化， 后边直接用Z进行了代换
如果把这个和MLF课程中的Regularization进行比较，其实都是对wTw进行了一些约束：
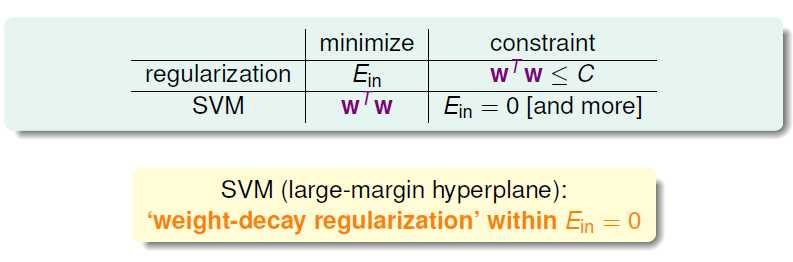本质是是相似的。
另外一种理解：如果我们把SVM中的约束看成一种筛选的算法，对于一个平面的若干点，
有可能一些margin不符合条件的划分方法会被忽略，那么，这实际上是降低了这个问题的VC维，这也是一种问题的优化方向。
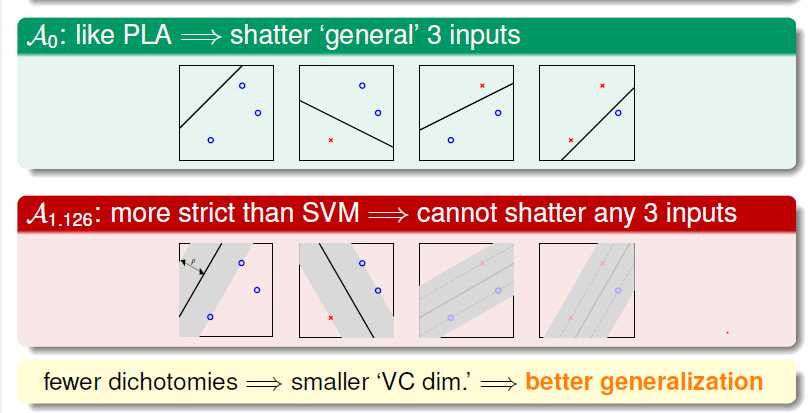
加了M > 1.126 的条件，相比于PLA则获得了更好的泛化性能。
以一个圆中点为例，有些划分情况在这个约束中无法达到，则我们得到了一个小于Dvc的新upper bound， 这部分约束的产生是和资料本身有关的。
这样，我们解决了一个模型复杂度要大和假设数量要少的矛盾问题：
接下来，我们将讨论非线性的SVM。
Machine Learning Techniques -1-Linear Support Vector Machine
标签：
原文地址：http://www.cnblogs.com/windniu/p/4746299.html
