标签:
前几天写了个模拟退火算法的程序,然后又陆陆续续看了很多群智能算法,发现很多旅行商问题都采用蚁群算法来求解,于是开始写蚁群算法的模板。网上关于蚁群算法的理论很多就不再这里赘述了,下面直接上代码和进行简单的比较。
c代码:

1 #ifndef _CITY_H 2 #define _CITY_H 3 struct CITY 4 { 5 int id; 6 double x, y; 7 }; 8 #endif // !_CITY_H

1 #ifndef _OPTION_H 2 #define _OPTION_H 3 const int MAXN = 210; 4 int m = 50; /* 蚂蚁数量 */ 5 double Q = 10; /* 常系数 */ 6 double alpha = 1; /* 信息素重要程度因子 */ 7 double beta = 5; /* 启发函数重要程度因子 */ 8 double rho = 0.2; /* 信息素挥发因子 */ 9 int iter = 1; /* 迭代次数初值 */ 10 int iter_max = 200; /* 最大迭代次数 */ 11 #endif // !_OPTION_H

1 #include <cstdio> 2 #include <cmath> 3 #include <ctime> 4 #include <set> 5 #include <vector> 6 #include <windows.h> 7 #include "CITY.h" 8 #include "OPTION.h" 9 using namespace std; 10 11 const double eps = 1e-4; 12 const double inf = (1 << 30); 13 const double rand_max = 32767; 14 CITY citys[MAXN]; /* 保存城市坐标和编号信息 */ 15 int city_count = 0; /* 保存城市数量 */ 16 double D[MAXN][MAXN]; /* 城市之间的距离矩阵 */ 17 double Heu_F[MAXN][MAXN]; /* 启发函数,Heu_F = 1./D (D为保存城市间距离的矩阵) */ 18 double Tau[MAXN][MAXN]; /* 信息素矩阵 */ 19 int Table[MAXN][MAXN]; /* 路径记录表 */ 20 int Route_best[MAXN][MAXN];/* 各代最佳路径 */ 21 double Length_best[MAXN]; /* 各代最佳路径的长度 */ 22 char *file = NULL; /* 数据文件 */ 23 time_t st, ed; /* 记录开始结束时间 */ 24 25 void put_help(); 26 void input(); 27 void cal_dist(); 28 void travel(); 29 int gen_int(); /* 随机生成城市编号 */ 30 double gen_rand(); /* 生成0~1之间的随机数 */ 31 void show_result(); 32 33 int main(int argc, char **argv) 34 { 35 36 srand(static_cast<int>(time(NULL))); 37 if (argc == 1) { 38 put_help(); 39 goto end; 40 } 41 /* get the parameters */ 42 file = argv[1]; 43 if (argc > 2) 44 { 45 for (int i = 2; i < argc; i += 2) { 46 if (strcmp(argv[i], "-m") == 0) { 47 m = atoi(argv[i + 1]); 48 } 49 else if (strcmp(argv[i], "-Q") == 0) { 50 Q = atof(argv[i + 1]); 51 } 52 else if (strcmp(argv[i], "-a") == 0){ 53 alpha = atof(argv[i + 1]); 54 } 55 else if (strcmp(argv[i], "-b") == 0) { 56 beta = atof(argv[i + 1]); 57 } 58 else if (strcmp(argv[i], "-r") == 0) { 59 rho = atof(argv[i + 1]); 60 } 61 else if (strcmp(argv[i], "-i") == 0) { 62 iter_max = atoi(argv[i + 1]); 63 } 64 } 65 } 66 file = argv[1]; 67 freopen(file, "r", stdin); 68 input(); 69 cal_dist(); 70 st = clock(); 71 travel(); 72 ed = clock(); 73 show_result(); 74 end: 75 return 0; 76 } 77 78 void put_help() 79 { 80 puts("用法: ACA 数据文件绝对路径 <参数设置> "); 81 puts("格式: ACA C:\\Users\\Administrator\\Desktop\\data.txt"); 82 puts("输入数据格式: 每行为城市的坐标"); 83 puts(" 1 2"); 84 puts(" 3 1"); 85 puts(" 5 6"); 86 puts("参数选项 "); 87 puts(" -m <int> 蚂蚁数量, 默认 50"); 88 puts(" -Q <double> 常系数, 默认 10"); 89 puts(" -a <double> 信息素重要程度因子, 默认1"); 90 puts(" -b <double> 启发函数重要程度因子, 默认5"); 91 puts(" -r <double> 信息素挥发因子, 默认0.2"); 92 puts(" -i <int > 最大迭代次数, 默认200"); 93 } 94 95 void input() 96 { 97 double x, y; 98 while (~scanf("%lf%lf", &x, &y)) { 99 ++city_count; 100 citys[city_count].id = city_count; 101 citys[city_count].x = x; 102 citys[city_count].y = y; 103 } 104 puts("Data input success!"); 105 } 106 107 void cal_dist() 108 { 109 for (int i = 1; i <= city_count; ++i) { 110 for (int j = 1; j <= city_count; ++j) { 111 D[i][j] = sqrt((citys[i].x - citys[j].x)*(citys[i].x - citys[j].x) 112 + (citys[i].y - citys[j].y)*(citys[i].y - citys[j].y)); 113 if (i == j) 114 D[i][j] = eps; 115 Heu_F[i][j] = 1 / D[i][j]; 116 } 117 } 118 } 119 120 int gen_int() 121 { 122 return rand() % city_count + 1; 123 } 124 125 void travel() 126 { 127 for (int i = 1; i <= city_count; ++i) 128 for (int j = 1; j <= city_count; ++j) 129 Tau[i][j] = 1; 130 while (iter <= iter_max) { 131 /* 随机产生各个蚂蚁的起点城市 */ 132 for (int i = 1; i <= m; ++i) 133 Table[i][1] = gen_int(); 134 /* 逐个蚂蚁路径选择 */ 135 for (int i = 1; i <= m; ++i) { 136 set<int> allow; /* 待访问城市集合 */ 137 vector<int> v_tabu; /* 禁忌表 */ 138 for (int k = 1; k <= city_count; ++k) { 139 if (k == Table[i][1]) 140 v_tabu.push_back(k); 141 else 142 allow.insert(k); 143 } 144 for (int j = 2; j <= city_count; ++j) { 145 double P[MAXN]; 146 P[0] = 0; 147 int allow_count = allow.size(); 148 auto k_it = allow.begin(); 149 auto tabu_it = v_tabu.end(); 150 --tabu_it; 151 /* 计算城市间转移概率 */ 152 for (int k = 1; k <= allow_count; ++k) { 153 P[k] = pow(Tau[*tabu_it][*k_it],alpha) 154 *pow(Heu_F[*tabu_it][*k_it],beta); 155 P[k] += P[k - 1]; 156 ++k_it; 157 } 158 /* 轮盘赌法选择下一个访问城市 */ 159 for (int k = 1; k <= allow_count; ++k) { 160 P[k] /= P[allow_count]; 161 } 162 double t_rand = gen_rand(); 163 int k; 164 for (k = 1; k <= allow_count; ++k) { 165 if (P[k] >= t_rand) 166 break; 167 } 168 auto allow_it = allow.begin(); 169 int cnt = 0; 170 while (cnt < k-1) { 171 ++cnt; 172 ++allow_it; 173 } 174 Table[i][j] = *allow_it; 175 v_tabu.push_back(Table[i][j]); 176 allow.erase(Table[i][j]); 177 } 178 } 179 /* 计算每个蚂蚁的路径距离 */ 180 double Length[MAXN]; 181 memset(Length, 0, sizeof Length); 182 for (int i = 1; i <= m; ++i) { 183 int Route[MAXN]; 184 for (int j = 1; j <= city_count; ++j) { 185 Route[j] = Table[i][j]; 186 } 187 for (int j = 1; j <= city_count - 1; ++j) { 188 Length[i] = Length[i] + D[Route[j]][Route[j + 1]]; 189 } 190 Length[i] = Length[i] + D[Route[city_count]][Route[1]]; 191 } 192 /* 计算最短路径距离和求最短路径 */ 193 if (iter == 1) { 194 double min_Length = static_cast<double>(inf); 195 for (int i = 1; i <= city_count; ++i) { 196 if (Length[i] < min_Length) { 197 min_Length = Length[i]; 198 for (int j = 1; j <= city_count; ++j) { 199 Route_best[iter][j] = Table[i][j]; 200 } 201 } 202 } 203 Length_best[iter] = min_Length; 204 } 205 else { 206 double min_Length = static_cast<double>(inf); 207 for (int i = 1; i <= city_count; ++i) { 208 if (Length[i] < min_Length) { 209 min_Length = Length[i]; 210 for (int j = 1; j <= city_count; ++j) { 211 Route_best[iter][j] = Table[i][j]; 212 } 213 } 214 } 215 Length_best[iter] = min_Length; 216 if (Length_best[iter-1] < min_Length) { 217 Length_best[iter] = Length_best[iter - 1]; 218 for (int j = 1; j <= city_count; ++j) { 219 Route_best[iter][j] = Route_best[iter-1][j]; 220 } 221 } 222 } 223 /* 更新信息素 */ 224 double Delta_Tau[MAXN][MAXN]; 225 for (int i = 1; i <= m; ++i) { 226 for (int j = 1; j <= city_count - 1; ++j) { 227 Delta_Tau[Table[i][j]][Table[i][j + 1]] 228 = Delta_Tau[Table[i][j]][Table[i][j + 1]] + Q / Length[i]; 229 } 230 Delta_Tau[Table[i][city_count]][Table[i][1]] 231 = Delta_Tau[Table[i][city_count]][Table[i][1]] + Q / Length[i]; 232 } 233 for (int i = 1; i <= city_count; ++i) 234 for (int j = 1; j <= city_count; ++j) 235 Tau[i][j] = (1 - rho)*Tau[i][j] + Delta_Tau[i][j]; 236 /* 迭代次数加1,清空路径记录表 */ 237 ++iter; 238 memset(Table, 0, sizeof Table); 239 } 240 } 241 242 double gen_rand() 243 { 244 return rand() / rand_max; 245 } 246 247 void show_result() 248 { 249 printf("求得的最短路径长度为: %lf\n", Length_best[iter_max]); 250 printf("最短路径为: "); 251 for (int i = 1; i <= city_count; ++i) { 252 printf("%d ", Route_best[iter_max][i]); 253 } 254 puts(""); 255 printf("程序运行时间: %lf s\n", static_cast<double>(ed - st) / CLOCKS_PER_SEC); 256 }
matlab代码:

1 %% 清空环境变量 2 clear all 3 clc 4 %% 导入数据 5 citys = [1304 2312 6 3639 1315 7 4177 2244 8 3712 1399 9 3488 1535 10 3326 1556 11 3238 1229 12 4196 1004 13 4312 790 14 4386 570 15 3007 1970 16 2562 1756 17 2788 1491 18 2381 1676 19 1332 695 20 3715 1678 21 3918 2179 22 4061 2370 23 3780 2212 24 3676 2578 25 4029 2838 26 4263 2931 27 3429 1908 28 3507 2367 29 3394 2643 30 3439 3201 31 2935 3240 32 3140 3550 33 2545 2357 34 2778 2826 35 2370 2975 36 ]; 37 %% 计算城市间相互距离 38 n = size(citys,1); 39 D = zeros(n,n); 40 for i = 1:n 41 for j = 1:n 42 if i ~= j 43 D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2)); 44 else 45 D(i,j) = 1e-4; 46 end 47 end 48 end 49 %% 初始化参数 50 m = 50; % 蚂蚁数量 51 alpha = 1; % 信息素重要程度因子 52 beta = 5; % 启发函数重要程度因子 53 rho = 0.2; % 信息素挥发因子 54 Q = 1; % 常系数 55 Eta = 1./D; % 启发函数 56 Tau = ones(n,n); % 信息素矩阵 57 Table = zeros(m,n); % 路径记录表 58 iter = 1; % 迭代次数初值 59 iter_max = 200; % 最大迭代次数 60 Route_best = zeros(iter_max,n); % 各代最佳路径 61 Length_best = zeros(iter_max,1); % 各代最佳路径的长度 62 Length_ave = zeros(iter_max,1); % 各代路径的平均长度 63 %% 迭代寻找最佳路径 64 tic 65 while iter <= iter_max 66 % 随机产生各个蚂蚁的起点城市 67 start = zeros(m,1); 68 for i = 1:m 69 temp = randperm(n); 70 start(i) = temp(1); 71 end 72 Table(:,1) = start; 73 % 构建解空间 74 citys_index = 1:n; 75 % 逐个蚂蚁路径选择 76 for i = 1:m 77 % 逐个城市路径选择 78 for j = 2:n 79 tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表) 80 allow_index = ~ismember(citys_index,tabu); 81 allow = citys_index(allow_index); % 待访问的城市集合 82 P = allow; 83 % 计算城市间转移概率 84 for k = 1:length(allow) 85 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta; 86 end 87 P = P/sum(P); 88 % 轮盘赌法选择下一个访问城市 89 Pc = cumsum(P); 90 target_index = find(Pc >= rand); 91 target = allow(target_index(1)); 92 Table(i,j) = target; 93 end 94 end 95 % 计算各个蚂蚁的路径距离 96 Length = zeros(m,1); 97 for i = 1:m 98 Route = Table(i,:); 99 for j = 1:(n - 1) 100 Length(i) = Length(i) + D(Route(j),Route(j + 1)); 101 end 102 Length(i) = Length(i) + D(Route(n),Route(1)); 103 end 104 % 计算最短路径距离及平均距离 105 if iter == 1 106 [min_Length,min_index] = min(Length); 107 Length_best(iter) = min_Length; 108 Length_ave(iter) = mean(Length); 109 Route_best(iter,:) = Table(min_index,:); 110 else 111 [min_Length,min_index] = min(Length); 112 Length_best(iter) = min(Length_best(iter - 1),min_Length); 113 Length_ave(iter) = mean(Length); 114 if Length_best(iter) == min_Length 115 Route_best(iter,:) = Table(min_index,:); 116 else 117 Route_best(iter,:) = Route_best((iter-1),:); 118 end 119 end 120 % 更新信息素 121 Delta_Tau = zeros(n,n); 122 % 逐个蚂蚁计算 123 for i = 1:m 124 % 逐个城市计算 125 for j = 1:(n - 1) 126 Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); 127 end 128 Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); 129 end 130 Tau = (1-rho) * Tau + Delta_Tau; 131 % 迭代次数加1,清空路径记录表 132 iter = iter + 1; 133 Table = zeros(m,n); 134 end 135 toc 136 %% 结果显示 137 [Shortest_Length,index] = min(Length_best); 138 Shortest_Route = Route_best(index,:); 139 disp([‘最短距离:‘ num2str(Shortest_Length)]); 140 disp([‘最短路径:‘ num2str([Shortest_Route Shortest_Route(1)])]); 141 %% 绘图 142 figure(1) 143 plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],... 144 [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],‘o-‘); 145 grid on 146 for i = 1:size(citys,1) 147 text(citys(i,1),citys(i,2),[‘ ‘ num2str(i)]); 148 end 149 text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),‘ 起点‘); 150 text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),‘ 终点‘); 151 xlabel(‘城市位置横坐标‘) 152 ylabel(‘城市位置纵坐标‘) 153 title([‘蚁群算法优化路径(最短距离:‘ num2str(Shortest_Length) ‘)‘]) 154 figure(2) 155 plot(1:iter_max,Length_best,‘b‘,1:iter_max,Length_ave,‘r:‘) 156 legend(‘最短距离‘,‘平均距离‘) 157 xlabel(‘迭代次数‘) 158 ylabel(‘距离‘) 159 title(‘各代最短距离与平均距离对比‘)
【运行结果比较】
测试数据选用和模拟退火的测试相同:
1304 2312
3639 1315
4177 2244
3712 1399
3488 1535
3326 1556
3238 1229
4196 1004
4312 790
4386 570
3007 1970
2562 1756
2788 1491
2381 1676
1332 695
3715 1678
3918 2179
4061 2370
3780 2212
3676 2578
4029 2838
4263 2931
3429 1908
3507 2367
3394 2643
3439 3201
2935 3240
3140 3550
2545 2357
2778 2826
2370 2975
c版ACA:
可选择设置的相关参数:
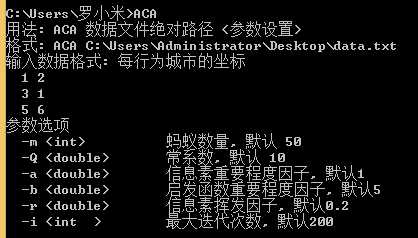
运行结果:



matlab版ACA:
运行结果:

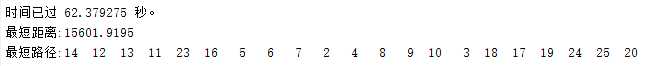
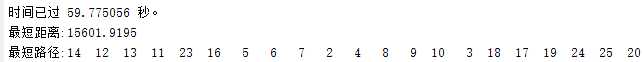
从时间效率上看,c运行时间比matlab的运行时间少了2/3,在运行之前就想到了,也没什么惊讶的,而且代码被我写搓了,继续优化可以更快。。。
然而多次运行c版的程序发现它貌似比matlab更容易陷入局部最优跳不出来,求得的路径长度基本都比matlab求出的路径长(。。。),百思不得其解,唯一能想到的是c++的伪随机数还不够“随机”导致陷入局部最优,还希望有大神解答下。
标签:
原文地址:http://www.cnblogs.com/ly941122/p/4747856.html