标签:
1、堆建立
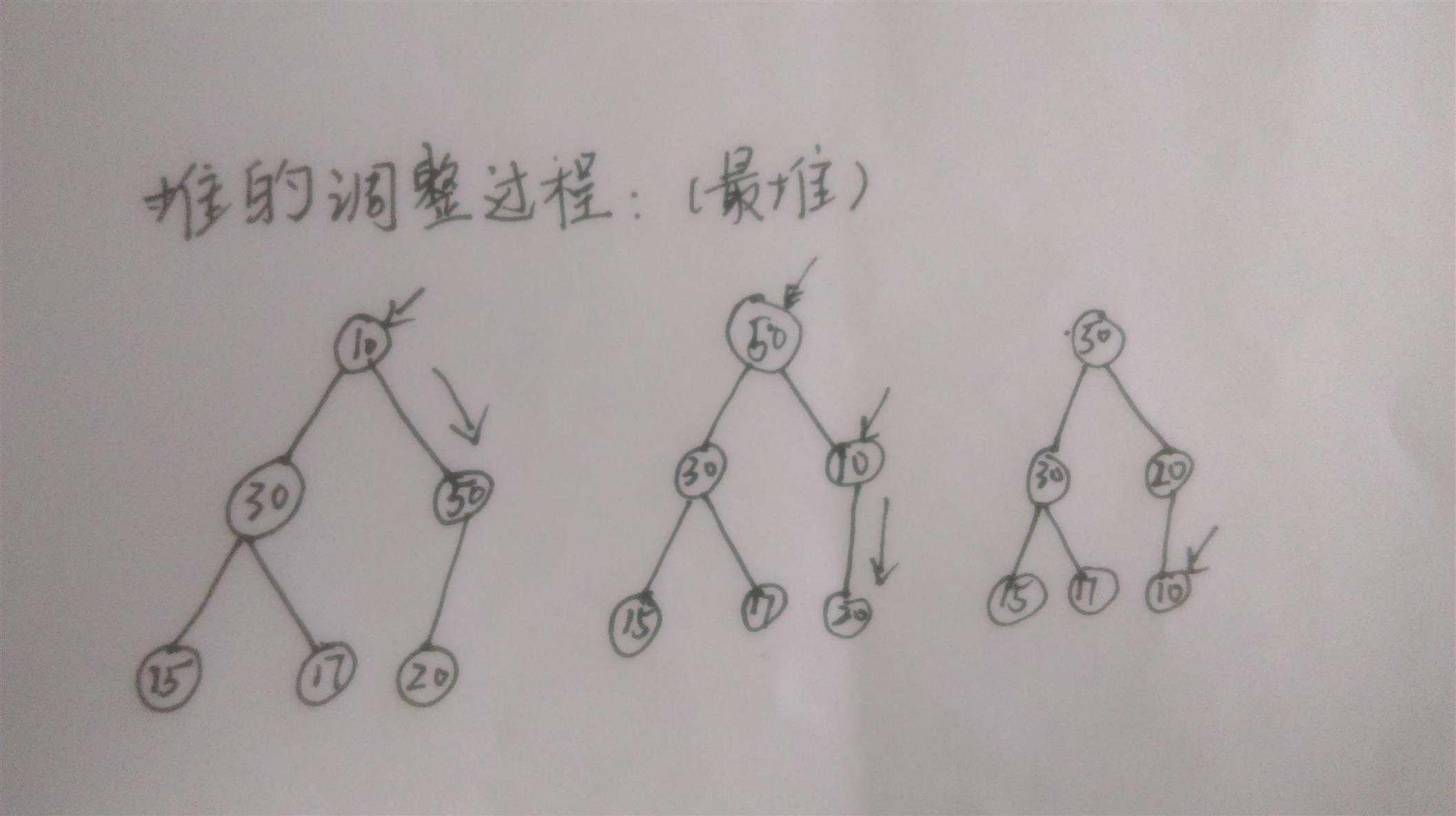
首先观察一个堆的向下调整过程。由于不满足最大堆的条件,对于不满足的元素,选择子节点中的最大元素交换。并更新被交换的子节点作为当前节点,继续调整,直至成为叶节点或满足最大堆的条件。
1 #define left(i) (2*i+1) 2 #define right(i) 2*(i+1) 3 #define parent(i) (i-1)/2 4 5 void _fix_down(int a[],int length, int index){ 6 int i =index; 7 int critical_node = (length-2)/2; 8 while(i<critical_node&&(a[i]<a[left(i)]||a[i]<a[right(i)])){ 9 int largest = i; 10 if(left(i)<length-1&&a[i]<a[left(i)]) 11 largest = left(i); 12 if(right(i)<length-1&&a[largest]<a[right(i)]) 13 largest = right(i); 14 if(largest!=i){ 15 swap(a[largest],a[i]); 16 i = largest; 17 } 18 } 19 }
则堆的建立过程如下,算法的思想是从非叶节点开始调整,直至根节点。
1 void build_heap(int a[],int length){ 2 int non_leaf = (length-2)/2; 3 for(int index = non_leaf;index>=0;index++) 4 _fix_down(a,length,index); 5 }
2、堆的插入
堆的插入是将数据插入至数组尾部,插入的数据有可能导致不满足最大堆的条件,所以我们需要有一个调整的过程。这个调整的过程称之为上溯。算法思想是对不满足的节点,与其父节点进行交换,更新父节点为当前节点,直至,满足条件或达到根节点。上溯的过程如下所示:
1 void _fix_up(int a[],int& length,int value){ 2 a[length] = value; 3 ++length; 4 int index = length-1; 5 while(index>0&&a[parent(index)]<a[index]){ 6 swap(a[index],a[parent(index)]); 7 index = parent(index); 8 } 9 }
3、堆排序
堆的排序相当于一个出堆的过程。在删除一个元素时,总是从根节点开始,并且是将根节点的元素与最尾部的元素相交换,减少堆的大小。并进行调整。不断的出堆,就会形成一个升序的堆。所以堆排序本质上是一个出堆的过程,如下所示:
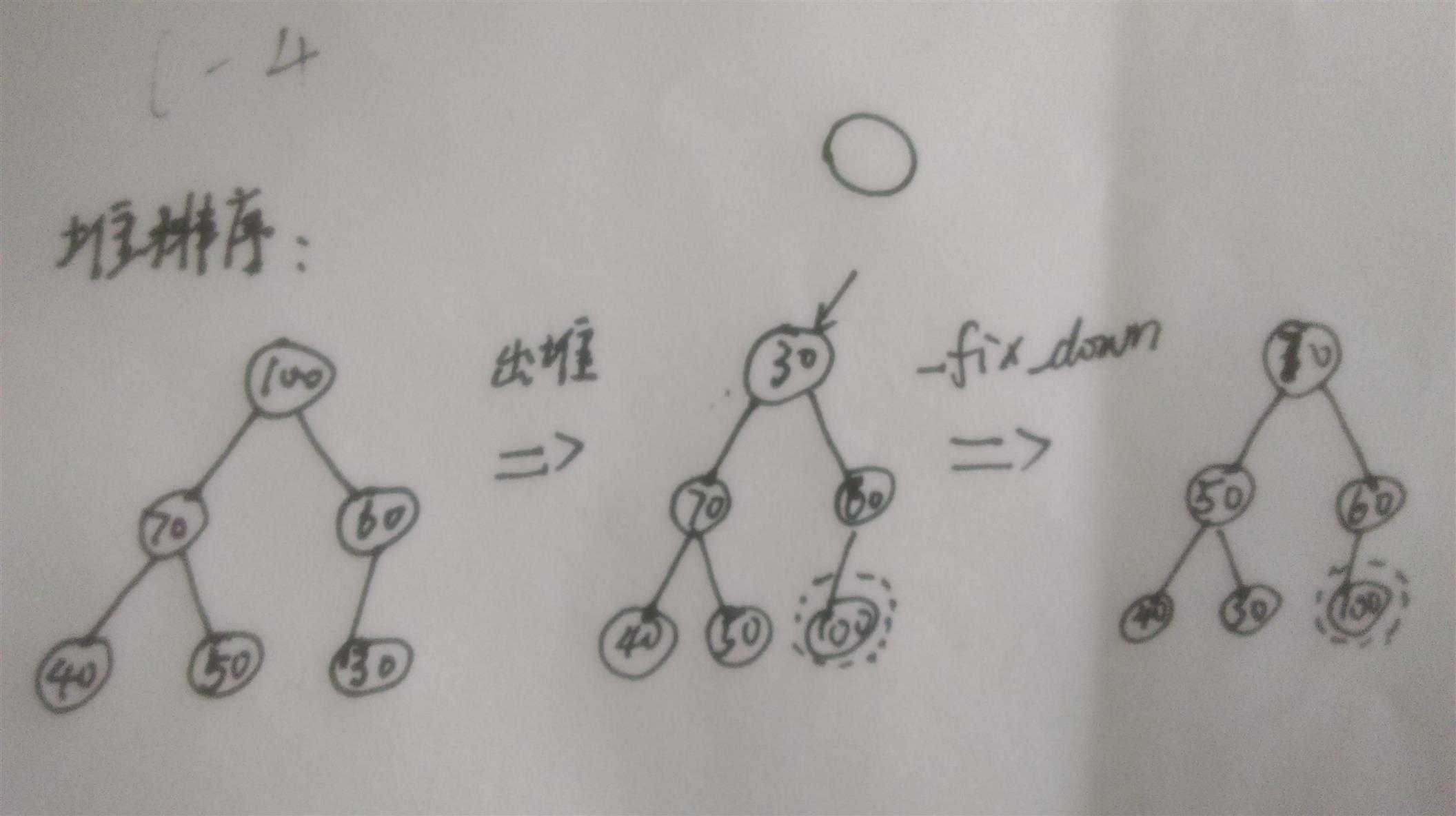
代码如下:
1 void heap_sort(int a[],int length){ 2 int index = length-1; 3 while(index>1){ 4 swap(a[0],a[index]); 5 _fix_down(a,index+1,0); 6 } 7 }
标签:
原文地址:http://www.cnblogs.com/zhang-wen/p/4761059.html