标签:
1.原理
冒泡排序法用于对乱序的数组元素进行排序。
假设数组长度为N:
1.从第1个元素开始,两两比较相邻元素的大小,如果前一个元素大于后一个元素,就调换两者位置(升序).
2.当所有相邻元素比较并换位后,最大的元素就排在位置N.
3.重复步骤1,从第1个元素开始两两比较,直到将第n-2个元素与第n-1个元素比较并换位(此时无需将第n-1个元素和第n个元素比较,因为第n个元素已经最大).
注:即第一次排序检查n-1次,第二次排序检查n-2次......最后一次只需检查1次
4.当只有第1个元素和第2个元素比较并排序时,排序完成.
2.示例
待排序数组:| 8 | 4 | 7 | 3 | 5 | 1 |
第一次外排序: 第二次外排序 第三次外排序
第一次比较:8>4,换位 第一次比较:4<7,不换位 第一次比较:4<3,换位
换位前:| 8 | 4 | 7 | 3 | 5 | 1 | 换位前:| 4 | 7 | 3 | 5 | 1 | 8 | 换位前:| 4 | 3 | 5 | 1 | 7 | 8 |
换位后:| 4 | 8 | 7 | 3 | 5 | 1 | 换位后:| 4 | 7 | 3 | 5 | 1 | 8 | 换位后:| 3 | 4 | 5 | 1 | 7 | 8 |
第二次比较:8>7,换位 第二次比较:7>3,换位 第二次比较:4<5,不换位
换位前:| 4 | 8 | 7 | 3 | 5 | 1 | 换位前:| 4 | 7 | 3 | 5 | 1 | 8 | 换位前:| 3 | 4 | 5 | 1 | 7 | 8 |
换位后:| 4 | 7 | 8 | 3 | 5 | 1 | 换位后:| 4 | 3 | 7 | 5 | 1 | 8 | 换位后:| 3 | 4 | 5 | 1 | 7 | 8 |
第三次比较:8>3,换位 第三次比较:7>5,换位 第三次比较:5>1,换位
换位前:| 4 | 7 | 8 | 3 | 5 | 1 | 换位前:| 4 | 3 | 7 | 5 | 1 | 8 | 换位前:| 3 | 4 | 5 | 1 | 7 | 8 |
换位后:| 4 | 7 | 3 | 8 | 5 | 1 | 换位前:| 4 | 3 | 5 | 7 | 1 | 8 | 换位后:| 3 | 4 | 1 | 5 | 7 | 8 |
第四次比较:8>5,换位 第四次比较:7>1,换位
换位前:| 4 | 4 | 3 | 8 | 5 | 1 | 换位前:| 4 | 3 | 5 | 7 | 1 | 8 |
换位后:| 4 | 7 | 3 | 5 | 8 | 1 | 换位后:| 4 | 3 | 5 | 1 | 7 | 8 |
第五次比较:8>1,换位
换位前:| 4 | 7 | 3 | 5 | 8 | 1 |
换位后:| 4 | 7 | 3 | 5 | 1 | 8 |
第四次外排序: 第五次外排序:
第一次比较:3<4,不换位 第一次比较:3<4,不换位
换位前:| 3 | 4 | 1 | 5 | 7 | 8 | 换位前:| 3 | 1 | 4 | 5 | 7 | 8 |
换位后:| 3 | 4 | 1 | 5 | 7 | 8 | 换位后:| 1 | 3 | 4 | 5 | 7 | 8 |
第二次比较:4>1,换位
换位前:| 3 | 4 | 1 | 5 | 7 | 8 |
换位后:| 3 | 1 | 4 | 5 | 7 | 8 |
3.时间复杂度
最好情况:序列是升序排列,在这种情况下,需要进行的比较操作为(n-1)次,交换操作为0次,即O(n)。
最坏情况:序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次,交换操作也是n(n-1)/2次次,即O(n^2)。
注:例如654321,需要将它排为654321,则只需要比较5次,此时顺序不变,不要进行第二次循环;当将它排为123456时,就要比较5+4+3+2+1次,换位5+4+3+2+1次。
4.动态演示

5.实例
public class BubbleSort {
public static void main(String args[]){
int i,j=0;
int a[]={8,4,7,3,5,1};
for(i=0;i<a.length-1;i++){
for(j=0;j<a.length-1-i;j++){
if(a[j]>a[j+1]){
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
for(i=0;i<6;i++){
System.out.println("a["+i+"]"+"="+a[i]);
}
}
}
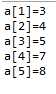

标签:
原文地址:http://www.cnblogs.com/jfl-xx/p/4760093.html