【POJ 1408】 Fishnet (叉积求面积)

标签：叉积求面积

【POJ 1408】 Fishnet (叉积求面积)

一个1*1㎡的池塘 有2*n条线代表渔网 问这些网中围出来的最大面积 一个有效面积是相邻两行和相邻两列中间夹的四边形

Input为n 后面跟着四行 每行n个浮点数 每一行分别代表a,b,c,d 

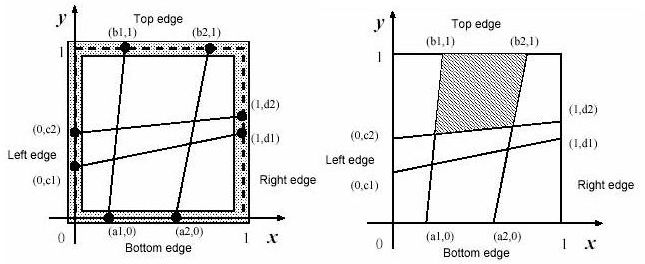
如图 并且保证a(i) > a(i-1) b(i) > b(i-1) c(i) > c(i-1) d(i) > d(i-1)

n(n <= 30)*2+4(四个岸)条边 枚举点数就行 相邻的四个四个点枚举 找出围出的最大面积

找点用叉乘即可 因为线段必定两两相交 因此不需要判断是否相交 直接用叉乘求交点即可 

然而观察可以发现坐标必定为(x2,0) (x1,1) (0,y1) (1,y2)

由(x2,0)或(x1,1)做平行与y轴的直线 由(0,y1)或(1,y2)做平行与x轴的直线

设两线交点为(x‘,y‘) 这样就可以发现相似关系

(x2-x1)*y‘ = x2-x‘

(y2-y1)*x‘ = y‘-y1

联立可得

y‘ = (x2*(y2 - y1) + y1)/((x2 - x1)*(y2 - y1) +1)

x‘ = (x2 - y1*(x2 - x1))/((x2 - x1)*(y2 - y1) + 1)

这样直接就可以求出来交点坐标

因为输入的规则是竖线从左到右 横线从下到上 因此枚举横线每个横线枚举竖线 然后由竖线i和i+1 横线j和j+1一定可以围出来一个四边形 球四变形面积用四个边两两的叉积(注意四个变都要用 即两次叉积以对顶角为起点) 叉积就是两边围出的平行四边形的面积 所以两叉积相加再除二就是四边围成的四边形的面积 不断枚举找出最大的就是答案

良心题 过了样例一般就A了 注意G++输出%f

代码如下:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#define esp 1e-8

using namespace std;

typedef struct Line Line;
typedef struct Point Point;

struct Point
{
    double x,y;
};

struct Line
{
    double x1,y1,x2,y2;

    Point operator ^ (const Line a)const//行^列求交
    {
        Point p;
        p.x = (a.x2 - y1*(a.x2 - a.x1))/((a.x2 - a.x1)*(y2 - y1) + 1);
        p.y = (a.x2*(y2 - y1) + y1)/((a.x2 - a.x1)*(y2 - y1) + 1);
        return p;
    }
};

Line h[32],l[32];

double xmult(double x1,double y1,double x2,double y2)
{
    return fabs(x1*y2-x2*y1);
}

int main()
{
    double ms,ans;
    Point p[4];
    int n,i,j;
    while(~scanf("%d",&n) && n)
    {
        l[0].x1 = l[0].x2 = 0;
        for(i = 1; i <= n; ++i) scanf("%lf",&l[i].x2);
        for(i = 1; i <= n; ++i) scanf("%lf",&l[i].x1);
        l[i].x1 = l[i].x2 = 1;

        h[0].y1 = h[0].y2 = 0;
        for(i = 1; i <= n; ++i) scanf("%lf",&h[i].y1);
        for(i = 1; i <= n; ++i) scanf("%lf",&h[i].y2);
        h[i].y1 = h[i].y2 = 1;

        ms = -1;
        for(i = 0; i <= n; ++i)
            for(j = 0; j <= n; ++j)
            {
                p[0] = h[i]^l[j];
                p[1] = h[i+1]^l[j+1];
                p[2] = h[i]^l[j+1];
                p[3] = h[i+1]^l[j];
                ans = (xmult(p[2].x-p[0].x,p[2].y-p[0].y,p[3].x-p[0].x,p[3].y-p[0].y)+xmult(p[2].x-p[1].x,p[2].y-p[1].y,p[3].x-p[1].x,p[3].y-p[1].y))/2;
                if(ans-ms > esp) ms = ans;
            }
        printf("%.6f\n",ms);
    }
    return 0;
}

【POJ 1408】 Fishnet (叉积求面积)

标签：叉积求面积

原文地址：http://blog.csdn.net/challengerrumble/article/details/48032367