标签:
KMP算法,是由Knuth,Morris,Pratt共同提出的模式匹配算法,其对于任何模式和目标序列,都可以在线性时间内完成匹配查找,而不会发生退化,是一个非常优秀的模式匹配算法。
举个例子来说,如果我想在字符串s(BBCABCEFABCDACEABCDACD)找是否存在子串t(ABCDABD)。
1.
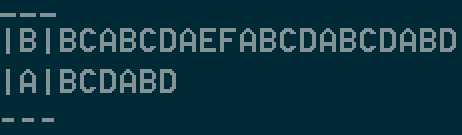
我们先去找匹配第一个字符,发现字符串s第一个字符与字符串t的第一个字符不匹配,然后我们继续往后找。
2.

知道搜到s的第4个字符才找到和t的第一个字符匹配的字符。
3.

然后我们继续一位位搜。
4.

直到我们搜到不能匹配的位置。
5.

正常想法是直接移一位,然后再从头开始逐个比较。这样做虽然可行,但效率太低。而这个就是KMP与众不同的地方。
当E和B不匹配的时候,你已经匹配了前5个,也就是说你知道t串前面6个的信息,KMP正是利用了这个已知信息,不把搜索位置移回已经比较过的位置,继续吧它向后移,这样就提高了效率。
6.

那么怎样往后移呢?,我们可以针对t建一张部分匹配表,那么这张表如何产生的呢?
"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,

(以上两图均出自参考文献)
附上伪代码:

1 nt[0] = 0; 2 int n = strlen(s); 3 for(int i = 1, j = 0; i < n; i ++){ 4 while(j != 0 && s[j] != s[i]) j = nt[j - 1]; 5 nt[i] = s[j] == s[i] ? ++ j : 0; 6 }
7.
然后,我们继续来看,我们发现最后一个匹配的字母为A,部分匹配值为1,根据移动公式:
移动位数 = 已匹配的字符数 - 对应的部分匹配值

5 - 1 = 4,所以向后移4位,变成上图。然后我们发现B和E仍旧不能匹配,此时算出需要移动位数为1,然后便有了下图。

之后我们发现A和E不能匹配,然后我们继续一位一位移,知道再找到一个A。
8.

然后我们又搜到了A,然后我们可以继续匹配啦。
9.
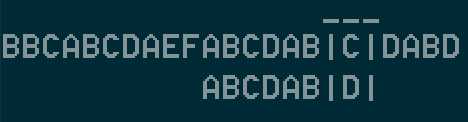
知道搜到最后一位(啊呀就差一点就能完全匹配,可惜),然后我们发现要移动4位。
10.
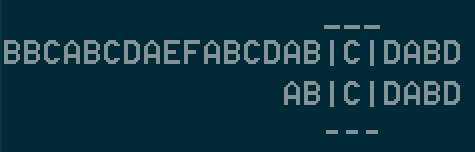
然后我们继续匹配,发现到最后刚好匹配完(好开心,找到了!)如下图:

附上总代码:

1 #include <cstdio> 2 #include <cstring> 3 const int N = 1000000 + 5; 4 char s[N]; 5 int nt[N]; 6 char t[N]; 7 8 void work(){ 9 nt[0] = 0; 10 int n = strlen(s); 11 for(int i = 1, j = 0; i < n; i ++){ 12 while(j != 0 && s[j] != s[i]) j = nt[j - 1]; 13 nt[i] = s[j] == s[i] ? ++ j : 0; 14 //printf("nt[%d] = %d\n", i, nt[i]); 15 } 16 int p = 0; 17 int q = 0; 18 int lt = strlen(t); 19 int ans = 0; 20 while(p + q < lt){ 21 if(s[p] == t[p + q]){ 22 while(s[p] == t[p + q] && p < n) p += 1; 23 //printf("p = %d\n", p); 24 if(p == n)ans += 1; 25 int w = p - nt[p - 1]; 26 p = nt[p - 1]; 27 q += w; 28 } 29 else { 30 while(p != 0 && s[p] != t[p + q]) p = nt[p - 1]; 31 q += 1; 32 } 33 } 34 printf("%d\n", ans); 35 } 36 37 int main() { 38 //while(scanf("%s%s", s, t) == 2) work(); 39 int T; 40 scanf("%d", &T); 41 while(T--){ 42 scanf("%s%s", s, t); 43 work(); 44 } 45 return 0; 46 }
参考文献:http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
标签:
原文地址:http://www.cnblogs.com/zyf0163/p/4774355.html