标签:
转载请注明出处:http://www.cnblogs.com/marc01in/p/4775440.html
和师弟师妹聊天时经常提及,若有志于从事数据挖掘、机器学习方面的工作,在大学阶段就要把基础知识都带上。 机器学习在大数据浪潮中逐渐展示她的魅力,其实《概率论》、《微积分》、《线性代数》、《运筹学》、《信息论》等几门课程算是前置课程,当然要转化为工程应用的话,编程技能也是需要的,而作为信息管理专业的同学,对于信息的理解、数据的敏感都是很好的加分项。
不过光说不练,给人的留下的印象是极为浅薄的,从一些大家都熟悉的角度切入,或许更容易能让人有所体会。
我很反感那些整天鼓吹”读书无用论“的人,因为高等教育传授的不仅仅是书面的知识,在大学的无所事事和忙碌充实是两种状态,也是每个人的选择,毕业时会发现同一个专业的同学,从事的工作千差万别,而这个造就差异的平台,就是大学。
以前多是做工程应用(游戏服务器、业务系统、BI),有段时间想回Amoy,换个工作方向,刚好工作中需要,也算整理一下吧。算法多是需要严谨的数学推导论证的,不过也不必担心学习过程的枯燥,等你看到结果的时候,你会发现生活处处是数学。
闲话扯的有点多,下面进入正题。
BTW,如果观点错误或者引用侵权的欢迎指正交流。
朴素贝叶斯,之所以称为朴素,是因为其中引入了几个假设(不用担心,下文会提及)。而正因为这几个假设的引入,使得模型简单易理解,同时如果训练得当,往往能收获不错的分类效果,因此这个系列以naive bayes开头和大家见面。
因为朴素贝叶斯是贝叶斯决策理论的一部分,所以我们先快速了解一下贝叶斯决策理论。
假设有一个数据集,由两类组成(简化问题),对于每个样本的分类,我们都已经知晓。数据分布如下图(图取自MLiA):
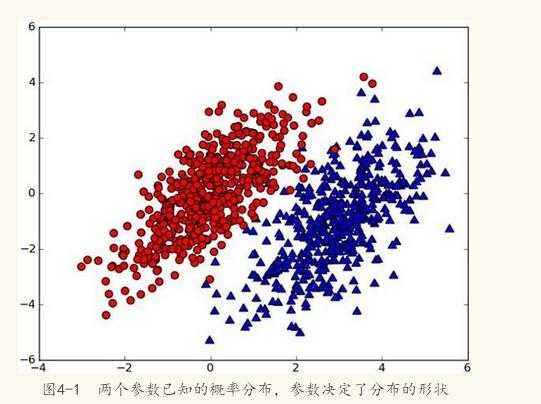
现在出现一个新的点new_point (x,y),其分类未知。我们可以用p1(x,y)表示数据点(x,y)属于红色一类的概率,同时也可以用p2(x,y)表示数据点(x,y)属于蓝色一类的概率。那要把new_point归在红、蓝哪一类呢?
我们提出这样的规则:
如果p1(x,y) > p2(x,y),则(x,y)为红色一类。
如果p1(x,y) <p2(x,y), 则(x,y)为蓝色一类。
换人类的语言来描述这一规则:选择概率高的一类作为新点的分类。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
用条件概率的方式定义这一贝叶斯分类准则:
如果p(red|x,y) > p(blue|x,y), 则(x,y)属于红色一类。
如果p(red|x,y) < p(blue|x,y), 则(x,y)属于蓝色一类。
也就是说,在出现一个需要分类的新点时,我们只需要计算这个点的
max(p(c1 | x,y),p(c2 | x,y),p(c3 | x,y)...p(cn| x,y))。其对于的最大概率标签,就是这个新点的分类啦。
那么问题来了,对于分类i 如何求解p(ci| x,y)呢?
没错,就是贝叶斯公式:
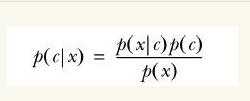
公式暂不推导,先描述这个转换的重要性。红色、蓝色分类是为了帮助理解,这里要换成多维度说法了,也就是第二部分的实例:判断一条微信朋友圈是不是广告。
前置条件是:我们已经拥有了一个平日广大用户的朋友圈内容库,这些朋友圈当中,如果真的是在做广告的,会被“热心网友”打上“广告”的标签,我们要做的是把所有内容分成一个一个词,每个词对应一个维度,构建一个高维度空间 (别担心,这里未出现向量计算)。
当出现一条新的朋友圈new_post,我们也将其分词,然后投放到朋友圈词库空间里。
这里的X表示多个特征(词)x1,x2,x3...组成的特征向量。
P(ad|x)表示:已知朋友圈内容而这条朋友圈是广告的概率。
利用贝叶斯公式,进行转换:
P(ad|X) = p(X|ad) p(ad) / p(X)
P(not-ad | X) = p(X|not-ad)p(not-ad) / p(X)
比较上面两个概率的大小,如果p(ad|X) > p(not-ad|X),则这条朋友圈被划分为广告,反之则不是广告。
看到这儿,实际问题已经转为数学公式了,但是怎么求解?好捉急。
看公式推导 (公式图片引用):
朴素贝叶斯分类的正式定义如下:
1、设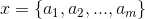 为一个待分类项,而每个a为x的一个特征属性。
为一个待分类项,而每个a为x的一个特征属性。
2、有类别集合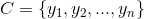 。
。
3、计算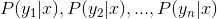 。
。
4、如果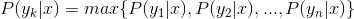 ,则
,则 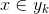 。
。
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做:
1、找到一个已知分类的待分类项集合,这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计。即。
3、如果各个特征属性是条件独立的,则根据贝叶斯定理有如下推导:
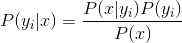
因为分母对于所有类别为常数,因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的,所以有:
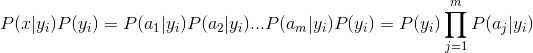
这里要引入朴素贝叶斯假设了。如果认为每个词都是独立的特征,那么朋友圈内容向量可以展开为分词(x1,x2,x3...xn),因此有了下面的公式推导:
P(ad|X) = p(X|ad)p(ad) = p(x1, x2, x3, x4...xn | ad) p(ad)
假设所有词相互条件独立,则进一步拆分:
P(ad|X) = p(x1|ad)p(x2|ad)p(x3|ad)...p(xn|ad) p(ad)
虽然现实中,一条朋友圈内容中,相互之间的词不会是相对独立的,因为我们的自然语言是讲究上下文的╮(╯▽╰)╭,不过这也是朴素贝叶斯的朴素所在,简单的看待问题。
看公式p(ad|X)=p(x1|ad)p(x2|ad)p(x3|ad)...p(xn|ad) p(ad)
至此,P(xi|ad)很容易求解,P(ad)为词库中广告朋友圈占所有朋友圈(训练集)的概率。我们的问题也就迎刃而解了。
到这里,应该已经有读者掀桌而起了,捣鼓半天,没有应用。 (╯‵□′)╯︵┻━┻
"Tall is cheap, show me the code."
逻辑均在代码注释中,因为用python编写,和伪代码没啥两样,而且我也懒得画图……

1 #encoding:UTF-8 2 ‘‘‘ 3 Author: marco lin 4 Date: 2015-08-28 5 ‘‘‘ 6 7 from numpy import * 8 import pickle 9 import jieba 10 import time 11 12 stop_word = [] 13 ‘‘‘ 14 停用词集, 包含“啊,吗,嗯”一类的无实意词汇以及标点符号 15 ‘‘‘ 16 def loadStopword(): 17 fr = open(‘stopword.txt‘, ‘r‘) 18 lines = fr.readlines() 19 for line in lines: 20 stop_word.append(line.strip().decode(‘utf-8‘)) 21 fr.close() 22 23 ‘‘‘ 24 创建词集 25 params: 26 documentSet 为训练文档集 27 return:词集, 作为词袋空间 28 ‘‘‘ 29 def createVocabList(documentSet): 30 vocabSet = set([]) 31 for document in documentSet: 32 vocabSet = vocabSet | set(document) #union of the two sets 33 return list(vocabSet) 34 35 ‘‘‘ 36 载入数据 37 ‘‘‘ 38 def loadData(): 39 return None 40 41 ‘‘‘ 42 文本处理,如果是未处理文本,则先分词(jieba分词),再去除停用词 43 ‘‘‘ 44 def textParse(bigString, load_from_file=True): #input is big string, #output is word list 45 if load_from_file: 46 listOfWord = bigString.split(‘/ ‘) 47 listOfWord = [x for x in listOfWord if x != ‘ ‘] 48 return listOfWord 49 else: 50 cutted = jieba.cut(bigString, cut_all=False) 51 listOfWord = [] 52 for word in cutted: 53 if word not in stop_word: 54 listOfWord.append(word) 55 return [word.encode(‘utf-8‘) for word in listOfWord] 56 57 ‘‘‘ 58 交叉训练 59 ‘‘‘ 60 CLASS_AD = 1 61 CLASS_NOT_AD = 0 62 63 def testClassify(): 64 listADDoc = [] 65 listNotADDoc = [] 66 listAllDoc = [] 67 listClasses = [] 68 69 print "----loading document list----" 70 71 #两千个标注为广告的文档 72 for i in range(1, 1001): 73 wordList = textParse(open(‘subject/subject_ad/%d.txt‘ % i).read()) 74 listAllDoc.append(wordList) 75 listClasses.append(CLASS_AD) 76 #两千个标注为非广告的文档 77 for i in range(1, 1001): 78 wordList = textParse(open(‘subject/subject_notad/%d.txt‘ % i).read()) 79 listAllDoc.append(wordList) 80 listClasses.append(CLASS_NOT_AD) 81 82 print "----creating vocab list----" 83 #构建词袋模型 84 listVocab = createVocabList(listAllDoc) 85 86 docNum = len(listAllDoc) 87 testSetNum = int(docNum * 0.1); 88 89 trainingIndexSet = range(docNum) # 建立与所有文档等长的空数据集(索引) 90 testSet = [] # 空测试集 91 92 # 随机索引,用作测试集, 同时将随机的索引从训练集中剔除 93 for i in range(testSetNum): 94 randIndex = int(random.uniform(0, len(trainingIndexSet))) 95 testSet.append(trainingIndexSet[randIndex]) 96 del(trainingIndexSet[randIndex]) 97 98 trainMatrix = [] 99 trainClasses = [] 100 101 for docIndex in trainingIndexSet: 102 trainMatrix.append(bagOfWords2VecMN(listVocab, listAllDoc[docIndex])) 103 trainClasses.append(listClasses[docIndex]) 104 105 print "----traning begin----" 106 pADV, pNotADV, pClassAD = trainNaiveBayes(array(trainMatrix), array(trainClasses)) 107 108 print "----traning complete----" 109 print "pADV:", pADV 110 print "pNotADV:", pNotADV 111 print "pClassAD:", pClassAD 112 print "ad: %d, not ad:%d" % (CLASS_AD, CLASS_NOT_AD) 113 114 args = dict() 115 args[‘pADV‘] = pADV 116 args[‘pNotADV‘] = pNotADV 117 args[‘pClassAD‘] = pClassAD 118 119 fw = open("args.pkl", "wb") 120 pickle.dump(args, fw, 2) 121 fw.close() 122 123 fw = open("vocab.pkl", "wb") 124 pickle.dump(listVocab, fw, 2) 125 fw.close() 126 127 errorCount = 0 128 for docIndex in testSet: 129 vecWord = bagOfWords2VecMN(listVocab, listAllDoc[docIndex]) 130 if classifyNaiveBayes(array(vecWord), pADV, pNotADV, pClassAD) != listClasses[docIndex]: 131 errorCount += 1 132 doc = ‘ ‘.join(listAllDoc[docIndex]) 133 print "classfication error", doc.decode(‘utf-8‘, "ignore").encode(‘gbk‘) 134 print ‘the error rate is: ‘, float(errorCount) / len(testSet) 135 136 # 分类方法(这边只做二类处理) 137 def classifyNaiveBayes(vec2Classify, pADVec, pNotADVec, pClass1): 138 pIsAD = sum(vec2Classify * pADVec) + log(pClass1) #element-wise mult 139 pIsNotAD = sum(vec2Classify * pNotADVec) + log(1.0 - pClass1) 140 141 if pIsAD > pIsNotAD: 142 return CLASS_AD 143 else: 144 return CLASS_NOT_AD 145 146 ‘‘‘ 147 训练 148 params: 149 tranMatrix 由测试文档转化成的词空间向量 所组成的 测试矩阵 150 tranClasses 上述测试文档对应的分类标签 151 ‘‘‘ 152 def trainNaiveBayes(trainMatrix, trainClasses): 153 numTrainDocs = len(trainMatrix) 154 numWords = len(trainMatrix[0]) #计算矩阵列数, 等于每个向量的维数 155 numIsAD = len(filter(lambda x: x == CLASS_AD, trainClasses)) 156 pClassAD = numIsAD / float(numTrainDocs) 157 pADNum = ones(numWords); pNotADNum = ones(numWords) 158 pADDenom = 2.0; pNotADDenom = 2.0 159 160 for i in range(numTrainDocs): 161 if trainClasses[i] == CLASS_AD: 162 pADNum += trainMatrix[i] 163 pADDenom += sum(trainMatrix[i]) 164 else: 165 pNotADNum += trainMatrix[i] 166 pNotADDenom += sum(trainMatrix[i]) 167 168 pADVect = log(pADNum / pADDenom) 169 pNotADVect = log(pNotADNum / pNotADDenom) 170 171 return pADVect, pNotADVect, pClassAD 172 173 ‘‘‘ 174 将输入转化为向量,其所在空间维度为 len(listVocab) 175 params: 176 listVocab-词集 177 inputSet-分词后的文本,存储于set 178 ‘‘‘ 179 def bagOfWords2VecMN(listVocab, inputSet): 180 returnVec = [0]*len(listVocab) 181 for word in inputSet: 182 if word in listVocab: 183 returnVec[listVocab.index(word)] += 1 184 return returnVec 185 186 ‘‘‘ 187 读取保存的模型,做分类操作 188 ‘‘‘ 189 def adClassify(text): 190 fr = open("args.pkl", "rb") 191 args = pickle.load(fr) 192 pADV = args[‘pADV‘] 193 pNotADV = args[‘pNotADV‘] 194 pClassAD = args[‘pClassAD‘] 195 fr.close() 196 197 fr = open("vocab.pkl", "rb") 198 listVocab = pickle.load(fr) 199 fr.close() 200 201 if len(listVocab) == 0: 202 print "got no args" 203 return 204 205 text = textParse(text, False) 206 vecWord = bagOfWords2VecMN(listVocab, text) 207 class_type = classifyNaiveBayes(array(vecWord), pADV, pNotADV, pClassAD) 208 209 print "classfication type:%d" % class_type 210 211 212 if __name__ == "__main__": 213 loadStopword() 214 while True: 215 opcode = raw_input("input 1 for training, 2 for ad classify: ") 216 if opcode.strip() == "1": 217 begtime = time.time() 218 testClassify() 219 print "cost time total:", time.time() - begtime 220 else: 221 text = raw_input("input the text:") 222 adClassify(text) 223
代码测试效果:
1、训练。
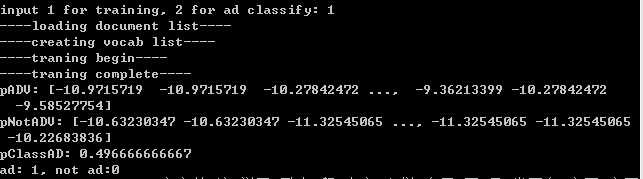

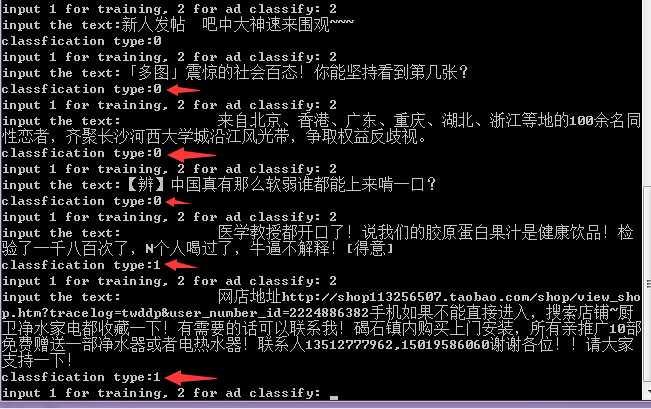
2、实例测试。
分类为1则归为广告,0为普通文本。
p.s.
此分类器的准确率,其实是比较依赖于训练语料的,机器学习算法就和纯洁的小孩一样,取决于其成长(训练)条件,“吃的是草挤的是奶”这种价值观其实是有些畸形的,毕竟“不是所有的牛奶,都叫特仑苏”。
标签:
原文地址:http://www.cnblogs.com/marc01in/p/4775440.html