标签:
RMQ问题:对于长度为N的序列,询问区间[L,R]中的最值
RMQ问题的几种解法:
简单介绍:
标准算法的实现:
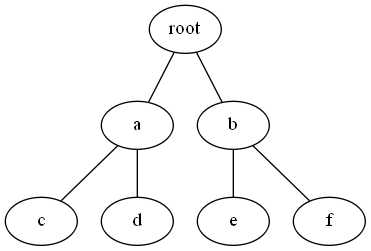
假设现在询问[d, f]的最小值,root为d和f的LCA,由笛卡尔树的性质可知,root是整棵树表示区间的最小值,而[d, f]是其子区间,所以root不可能比[d, f]中的数小,又因为d和f属于root的不同子树(LCA的性质),所以root一定在[d, f]中(笛卡尔树的性质),故对两个点a,b,LCA(a, b)就是[a, b]的最小值,证毕。
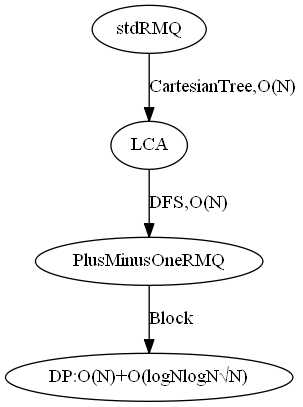
标准RMQ,O(N)-O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 |
struct PlusMinusOneRMQ { const static int N = 223456; const static int M = 15; int blocklen, block, minv[N], dp[N][20], t[N * 20], f[1 << M][M][M], s[N]; void init(int n) { blocklen = max(1, (int)(log(n * 1.0) / log(2.0)) / 2); block = n / blocklen + (n % blocklen > 0); int total = 1 << (blocklen - 1); for (int i = 0; i < total; i ++) { for (int l = 0; l < blocklen; l ++) { f[i][l][l] = l; int now = 0, minv = 0; for (int r = l + 1; r < blocklen; r ++) { f[i][l][r] = f[i][l][r - 1]; if ((1 << (r - 1)) & i) now ++; else { now --; if (now < minv) { minv = now; f[i][l][r] = r; } } } } } int tot = N * 20; t[1] = 0; for (int i = 2; i < tot; i ++) { t[i] = t[i - 1]; if (!(i & (i - 1))) t[i] ++; } } void initmin(int a[], int n) { for (int i = 0; i < n; i ++) { if (i % blocklen == 0) { minv[i / blocklen] = i; s[i / blocklen] = 0; } else { if (a[i] < a[minv[i / blocklen]]) minv[i / blocklen] = i; if (a[i] > a[i - 1]) s[i / blocklen] |= 1 << (i % blocklen - 1); } } for (int i = 0; i < block; i ++) dp[i][0] = minv[i]; for (int j = 1; (1 << j) <= block; j ++) { for (int i = 0; i + (1 << j) - 1 < block; i ++) { int b1 = dp[i][j - 1], b2 = dp[i + (1 << (j - 1))][j - 1]; dp[i][j] = a[b1] < a[b2]? b1 : b2; } } } int querymin(int a[], int L, int R) { int idl = L / blocklen, idr = R / blocklen; if (idl == idr) return idl * blocklen + f[s[idl]][L % blocklen][R % blocklen]; else { int b1 = idl * blocklen + f[s[idl]][L % blocklen][blocklen - 1]; int b2 = idr * blocklen + f[s[idr]][0][R % blocklen]; int buf = a[b1] < a[b2]? b1 : b2; int c = t[idr - idl - 1]; if (idr - idl - 1) { int b1 = dp[idl + 1][c]; int b2 = dp[idr - 1 - (1 << c) + 1][c]; int b = a[b1] < a[b2]? b1 : b2; return a[buf] < a[b]? buf : b; } return buf; } } }; struct CartesianTree { private: struct Node { int key, value, l, r; Node(int key, int value) { this->key = key; this->value = value; l = r = 0; } Node() {} }; Node tree[maxn]; int sz; int S[maxn], top; /** 小根堆 区间最小值*/ public: void build(int a[], int n) { top = 0; tree[0] = Node(-1, 0x80000000);//将根的key和value赋为最小以保持树根不变 S[top ++] = 0; sz = 0; for (int i = 0; i < n; i ++) { tree[++ sz] = Node(i, a[i]); int last = 0; while (tree[S[top - 1]].value >= tree[sz].value) { last = S[top - 1]; top --; } tree[sz].l = last; tree[S[top - 1]].r = sz; S[top ++] = sz; } } Node &operator [] (const int x) { return tree[x]; } };/** 树根为定值0,数组从0开始编号 **/ class stdRMQ { public: void work(int a[], int n) { ct.build(a, n); dfs_clock = 0; dfs(0, 0); rmq.init(dfs_clock); rmq.initmin(depseq, dfs_clock); } int query(int L, int R) { int cl = clk[L], cr = clk[R]; if (cl > cr) swap(cl, cr); return value[rmq.querymin(depseq, cl, cr)]; } private: CartesianTree ct; PlusMinusOneRMQ rmq; int dfs_clock, clk[maxn], value[maxn << 1], depseq[maxn << 1]; void dfs(int rt, int d) { clk[ct[rt].key] = dfs_clock; depseq[dfs_clock] = d; value[dfs_clock ++] = ct[rt].value; if (ct[rt].l) { dfs(ct[rt].l, d + 1); depseq[dfs_clock] = d; value[dfs_clock ++] = ct[rt].value; } if (ct[rt].r) { dfs(ct[rt].r, d + 1); depseq[dfs_clock] = d; value[dfs_clock ++] = ct[rt].value; } } }; |
标签:
原文地址:http://www.cnblogs.com/jklongint/p/4777448.html