标签:
前言:学习图的遍历算法之前,需要先了解一下图的存储方式(这里只以无向图作为讨论了)。
(1)邻接矩阵
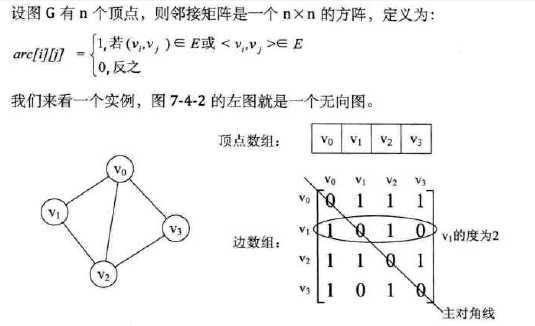
(2)邻接表
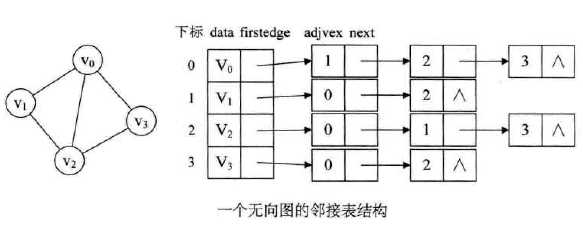
一、DFS(深度优先遍历)
设置一个visited数组防止重复遍历,DFS主要利用的是栈结构
邻接矩阵的遍历
#include<iostream>
using namespace std;
const int n=4;//图中顶点的数量
struct graph
{
char v[n+1];//顶点信息
int arcs[n+1][n+1];//邻接矩阵
};
graph g;
bool visited[n+1];//用来标记结点是否被访问过
void dfs(int i)
{
cout<<g.v[i]<<endl;
visited[i]=true;
for(int j=1;j<=n;j++)
{
if(g.arcs[i][j]==1 && visited[j]==false)
{
dfs(j);
}
}
}
int main()
{
memset(visited,false,sizeof(visited));
//测试
for(int i=1;i<=4;i++)
{
g.v[i]=i+‘A‘-1;
}
for(int i=1;i<=4;i++)
{
for(int j=1;j<=4;j++)
{
g.arcs[i][j]=0;
}
}
g.arcs[1][2]=g.arcs[2][1]=1;
g.arcs[2][3]=g.arcs[3][2]=1;
g.arcs[2][4]=g.arcs[4][2]=1;
dfs(1);
return 0;
}
二、BFS(广度优先遍历)
设置一个visited数组防止重复遍历,DFS主要利用的是队列结构
#include<iostream> #include<queue> using namespace std; const int n=4;//图中顶点的数量 struct graph { char v[n+1];//顶点信息 int arcs[n+1][n+1];//邻接矩阵 }; graph g; queue<int>q; bool visited[n+1];//用来标记结点是否被访问过 void bfs(int i) { visited[i]=true; q.push(i); while(!q.empty()) { for(int j=1;j<=n;j++) { if(g.arcs[q.front()][j]==1 && visited[j]==false) { visited[j]=true; q.push(j); } } cout<<g.v[q.front()]<<endl; q.pop(); } } int main() { memset(visited,false,sizeof(visited)); //测试 for(int i=1;i<=4;i++) { g.v[i]=i+‘A‘-1; } for(int i=1;i<=4;i++) { for(int j=1;j<=4;j++) { g.arcs[i][j]=0; } } g.arcs[1][2]=g.arcs[2][1]=1; g.arcs[2][3]=g.arcs[3][2]=1; g.arcs[2][4]=g.arcs[4][2]=1; bfs(1); return 0; }
标签:
原文地址:http://www.cnblogs.com/bewolf/p/4776887.html