标签:
这一题是最近在看Coursera的《算法与设计》的公开课时看到的一道较难的DP例题,之所以写下来,一方面是因为DP的状态我想了很久才想明白,所以借此记录,另一方面是看到这一题有运用到 排列计数 的方法,虽然排列计数的思路简单,但却是算法中一个数学优化的点睛之笔。
Poj1037 A decorative fence
题意:有K组数据(1~100),每组数据给出总木棒数N(1~20)和一个排列数C(64位整型范围内),N个木棒长度各异,按照以下条件排列,并将所有可能结果进行字典序排序
1.每一个木棒两侧木棒的长度都比该木棒长或者短(除该木棒在两端处外)
2.木棒由小到大进行排序,完成1中排列后得到的排列即为结果,将所有结果进行字典序排序。
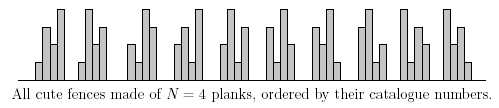
现在求总木棒数为N时,排列数为C的结果。
大致思路:利用动态规划构造排列状态打出1~20的排列数表,然后根据排列计数的原理找到排列数为C的排列用数组存储并输出。
构造三维DP数组:dp[n][i][2]-n木棒下,最新插入的第 i 短木棒的可能方案数
数组第三维具体表述:dp[n][i][DOWN]:第 i 短木棒以下降状态插入 | dp[n][i][UP]:第 i 短木棒以上升状态插入
构建三维DP的状态转移方程 dp[n][i][UP] = ∑(dp[n-1][k][DOWN]) (k = 1,2...i-1) //所有n-1木棒时的下降状态之和-得到n木棒时的上升状态DP值
dp[n][i][DOWN] = ∑(dp[n-1][k][UP]) (k = i,i+1...n-1) //所有n-1木棒时的上升状态之和-得到n木棒时的下降状态DP值
排列计数:
这一题中如果我们已经知道n个木棒的排列数,我们应该如何去求第C个排列的状态呢?
难道我们要列出所有的排列状态,然后排序后去找吗,显然这是一种很愚蠢的做法,不仅代码冗长,而且耗时较长,所以这里需要我们进行查找排列数的优化。
例子:
举个例子,如果我们知道1!,2!,3!,4!...的值,现在求1~5的全排列中第41个排列数是多少该怎么求呢?
其实我们可以简单想想如果第一位数是1的话,后面还有2~5总计4个数的全排列,因此首位是1的排列数有4! = 24种方案,24<41,因此首位一定不是1,
现在首位为1的情况要排除掉,我们首位从2开始,现在剩余要找到的排列数是41-24 = 17了,而首位为2的排列数也是24种,24>17,因此首位一定是2了,
首位确定了,我们就可以找第二位了,首先从1开始,后面还有三位数排列,因此排列数共3! = 6,6<17,因此第二位一定不是1了,
所以我们第二位从没有确定的3开始,现在要找寻的排列数是17-6=11....
以此类推,我们就可以找到第41种排列情况是24513,这样的最坏时间度为O(n2)
那么这一题也可以采用类似的简单排列计数算法
最终 Code 如下:

1 //Memory:180K Time:0 Ms 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 using namespace std; 6 7 #define MAX 21 8 9 enum State{ 10 DOWN, //下降状态 11 UP, //上升状态 12 }; 13 14 __int64 dp[MAX][MAX][2]; //所有状态 15 int permut[MAX]; //答案排列-permutation 16 int v[MAX]; 17 18 void DP(int n) //初始DP-dp[i][j][]-为bar共 i 个时,最新insert木棒 j 的总情况数 19 { 20 dp[1][1][DOWN] = dp[1][1][UP] = 1; 21 for (int i = 2; i <= n; i++) //现有bar数 22 for (int j = 1; j <= i; j++) //最新insert的bar M (第j短) 23 { 24 for (int k = j; k < i; k++) //+all可达此上升态的上一个状态(下降)DP值(k >= j) 25 dp[i][j][UP] += dp[i - 1][k][DOWN]; 26 for (int k = 1; k < j; k++) //+all可达此下降态的上一个状态(上升)DP值(k < j) 27 dp[i][j][DOWN] += dp[i - 1][k][UP]; 28 } 29 return; 30 } 31 32 void Find_permutation(int n, __int64 c) 33 { 34 memset(v, 0, sizeof(v)); 35 memset(permut, 0, sizeof(permut)); 36 for (int i = 1; i <= n; i++) 37 { 38 __int64 skip = 0; //跳过方案数 39 int No = 0; 40 for (int cur = 1; cur <= n; cur++) //第cur短的bar 41 { 42 if (!v[cur]) 43 { 44 No++; //cur在剩余木棒中第No短 45 if (i == 1) 46 skip = dp[n][No][UP] + dp[n][No][DOWN]; //No==1 47 else 48 { 49 //题意条件+排列计数知识 50 if (cur > permut[i - 1] && (i == 2 || permut[i - 2] > permut[i - 1])) 51 skip = dp[n-i+1][No][DOWN]; //前一所有下降状态-达到当前上升状态 52 else if (cur < permut[i - 1] && (i == 2 || permut[i - 2] < permut[i - 1])) 53 skip = dp[n-i+1][No][UP]; //前一所有上升状态-达到当前下降状态 54 } 55 if (skip >= c) 56 { 57 v[cur] = 1; 58 permut[i] = cur; 59 break; 60 } 61 else 62 c -= skip; 63 } 64 } 65 } 66 /* PRINT */ 67 for (int i = 1; i <= n; i++) 68 printf("%d ", permut[i]); 69 printf("\n"); 70 } 71 72 int main() 73 { 74 int T, n; 75 __int64 c; 76 77 DP(20); 78 79 scanf("%d", &T); 80 while (T--) 81 { 82 scanf("%d%I64d", &n, &c); 83 84 Find_permutation(n, c); 85 } 86 87 return 0; 88 }
ACM/ICPC算法训练 之 数学很重要-浅谈“排列计数” (DP题-POJ1037)
标签:
原文地址:http://www.cnblogs.com/Inkblots/p/4789886.html