【POJ 3321】 Apple Tree (dfs重标号设区间+树状数组求和)

标签：

【POJ 3321】 Apple Tree (dfs重标号设区间+树状数组求和)

Description

There is an apple tree outside of kaka‘s house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

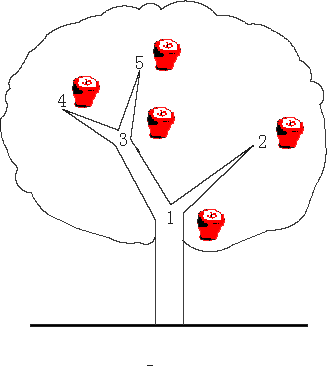
The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won‘t grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

Input

Output

Sample Input

3
1 2
1 3
3
Q 1
C 2
Q 1

Sample Output

3
2

Source

题目大意是一棵树 1~n个苹果 两个苹果间由树枝连接 并保证编号1的苹果是根 并且满足树结构(一个节点只有一个父亲)

然后有两种操作 

Q x 问编号x的子树上共几颗苹果

C x 如果x苹果还在 摘掉它(它所在的子树上苹果数减一) 如果被摘掉了 就再长出来个(所在子树上的苹果数加一)

由于只知道1是根 其他不确定链接顺序 所以先邻接表存图 为了实现区间查询 dfs重标号 让父亲比孩子编号大 这样父亲管辖的区间很容易表示出来(dfs是连续过程 每个节点子所有儿子遍历完才回溯 保证了区间连续性)

这样重标号后用树状数组累加苹果数即可 Q x时用x查值 - (x子数最后节点编号+1)的查值即可 这就是父亲比儿子编号大的原因 树状数组累加时从高向低 所以从大到小编号可满足

代码如下:

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>

using namespace std;

typedef struct Edge
{
    int v,next;
}Edge;

Edge eg[200200];
int head[100100];//邻接表存图
int f[100100],en[100100];//重标号区间首尾
int tr[100100];//树状数组
bool vis[100100];//访问标记
int n,tp,id;//n-节点个数 tp-邻接表指针 id-dfs重标号编号

int Lowbite(int x)
{
    return x&(-x);
}

void Ad(int x,int data)
{
    while(x <= n)
    {
        tr[x] += data;
        x += Lowbite(x);
    }
}

int Sum(int x)
{
    int ans = 0;
    while(x)
    {
        ans += tr[x];
        x -= Lowbite(x);
    }
    return ans;
}

void Add(int u,int v)//加边
{
    eg[tp].v = v;
    eg[tp].next = head[u];
    head[u] = tp++;
}

void dfs(int u)
{
    Ad(id,1);
    vis[u] = 1;
    f[u] = id--;
    int i,v;
    for(i = head[u]; i != -1; i = eg[i].next)
    {
        v = eg[i].v;
        if(vis[v]) continue;
        dfs(v);
    }
    en[f[u]] = id;//u子树遍历完后 id即为其区间最后一位+1
}

int main()
{
    int m,i,x,u,v;
    char ch[3];
    memset(head,-1,sizeof(head));
    tp = 0;

    scanf("%d",&n);
    for(i = 0; i < n-1; ++i)
    {
        scanf("%d %d",&u,&v);
        Add(u,v);
        Add(v,u);
    }

    id = n;//id初始最大编号
    memset(vis,0,sizeof(vis));
    dfs(1);

    scanf("%d",&m);
    memset(vis,0,sizeof(vis));
    while(m--)
    {
        scanf("%s%d",ch,&x);
        if(ch[0] == 'C')
        {
            if(vis[x])//苹果被摘掉了 重生
            {
                Ad(f[x],1);
                vis[x] = 0;
            }
            else//有苹果 摘掉
            {
                Ad(f[x],-1);
                vis[x] = 1;
            }
        }
        else printf("%d\n",Sum(f[x])-Sum(en[f[x]]));
    }

    return 0;
}

【POJ 3321】 Apple Tree (dfs重标号设区间+树状数组求和)

标签：

原文地址：http://blog.csdn.net/challengerrumble/article/details/48328379