标签:
ACM的在线测试里经常涉及到大量数据的的修改,求和等操作,这里介绍一种方法——树状数组。
树状数组,是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只能查询其中一个元素的值。可以用一张图来弄懂什么是数组数组。
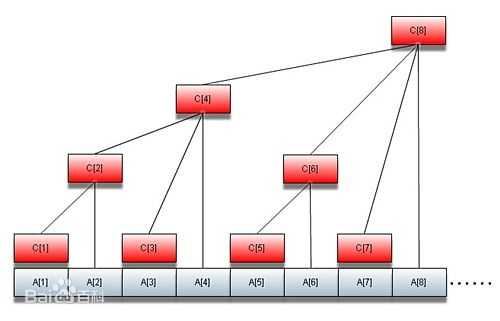
原数组A[n],树状数组C[n];
如果n为奇数:Cn=An;
如果n为偶数:Cn = A(n – 2^k + 1) + ... + An,k为n的二进制数末尾0的个数。
可以用lowbit函数快速得到2^k,这里用到了位运算,&是位运算符,不细说。
int lowbit(int t)
{
return t&(-t);
}
该函数返回该树状数组节点的管辖范围,如C[6],带入6返回值为2,C[6]=A[5]+A[6];
更新树状数组函数upDate
void upDate(int x,int num) //修改树状数组
{
while(x<=N)
{
b[x]+=num;
x+=lowbit(x);
}
}
x是要更新的节点,N为树状数组长度,num为修改的值,本函数将树状数组C[]中所有包含A[x]的节点更新。本函数可用于数组的修改,也可用于数组的建立。
求和函数getSum
int getSum(int x) //求0-x的和
{
int s=0;
while(x>0)
{
s+=b[x];
x-=lowbit(x);
}
return s;
}
如果要求数组m-n段的和可用getSum(n)-getSum(m);
有了以上三个函数最基本的树状数组就成型了。。
再深入。。。。。
我也无能为力了。。。
标签:
原文地址:http://www.cnblogs.com/wuyoucao/p/4814200.html