标签:
今天参加笔试,遇见一道编程题,给定一个1~9的整数N代表熊的数目,每只熊按照如下方式分苹果:先将苹果平均分为N份,再扔掉一个。要求输出最少的苹果总数?
思路1:逐层向下,设总数为X,则第一次每一份为(X-1)/N个苹果,第二次为((N-1)*((X-1)/N)-1)/N,依次类推.......,发现到最后由于嵌套的层数过多,已经被弄晕了,果断换方法。
思路2:(采取补苹果的方法)由题描述,因为要扔一个苹果,所以扔一个苹果==补N-1个苹果,因此第一个熊得到的苹果数为(X+N-1)/N,第二个熊得到的为(N-1)*(X+N-1)/(N*N),。。。。第N个熊为(N-1)的(N-1)次方*(X+N-1)/N的N次方。
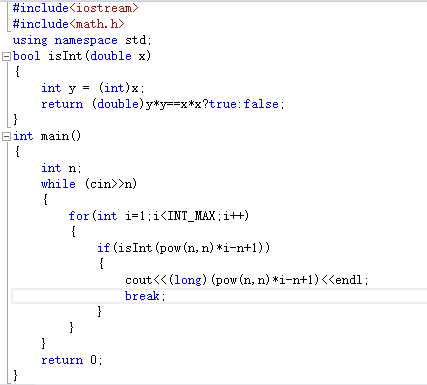
由于熊肯定得到的是整数个苹果,所以第N个熊的苹果数(N-1)的(N-1)次方*(X+N-1)/N的N次方必为一个整数。很显然(N-1)的(N-1)次方/N的N是不可能整除的,因此(X+N-1)必为N的N次方的整数倍,我们主需要去尝试当(X+N-1) = k倍的N的N次方即可,k从1开始走起,遇到第一个满足(X+N-1) = k倍的N的N次方的k时,对应的x即为最少的苹果数。
基于上面思想:有如下代码
标签:
原文地址:http://www.cnblogs.com/llf-hwj/p/4820411.html