标签:
摘 要: 本文前半部分主要是关于Erlang编程语言相关的内容;着重就一般学习编程语言的一般的关注点来阐述了Erlang编程语言的基本语法点,主要包括:Erlang的变量、Erlang的数据类型、Erlang的语句和Erlang编程语言的函数与模块四个方面;本文的后半部分主要就Erlang语言的并行化编程的实践:Erlang的并行化编程与Erlang并行化编程在矩阵乘积的实际应用,通过实践,可以发现,Erlang语言确实在并行化编程方面表现得很优秀。
关键词:并行计算;Erlang;编程语言;矩阵相乘
自从计算机出现的时候开始,其就迅速发展。短暂的几十年,计算机已经从当初的单核走过,向多核发展,直到现在的多机系统。提升计算机的计算性能和计算速率一直是计算机发展的不变的主题,但是随着单位面积晶体管数目的饱和,单纯的以晶体管的数目来衡量计算机的发展水平已经成为过去,单纯地以增加单位面积晶体管的数目来提升计算的性能已经走到了尽头,就像C++标准委员会主席Herb Sutter所说的那样我们的《免费的午餐已经结束》,计算机的发展开始向着多核的方向发展,但是为了达到一定的计算速率,仅仅是依靠多核来提升的代价是昂贵的,且依靠这样的方式有一定的局限性。为了节省成本与得到更大的计算性能,多机系统逐渐出现。利用多个一般的计算核心来组成计算机集群进行并行计算或分布式计算来提升计算的能力,得到更高的计算能力。一个典型的应用的例子就是云计算。Google实践表明,用廉价的服务器组成的服务器集群,在计算能力、可靠性等方面达到了价格昂贵的大型计算机的水准,毫无疑问,这是大型、超大型网站和网络应用的福音。
在国家发展方面,高性能计算的发展也是必要的。目前,如气象、 石油勘探、生物制药、核爆模拟等国家命脉的科学研究,都离不开高性能大规模的并行计算。在这些科研活动中,需要大量的科学计算。提升在这些科学研究中的计算就是提升我国的综合实力,极大提升我国在国际中的地位。
目前发展的大趋势是并行计算。为了重新利用目前的并行化硬件资源,需要并行化的软件编程语言支持。Herb Sutter曾表示,如果一门语言不能够以优雅可靠的方式处理并行计算的问题,那它就失去在21世纪的生存权。“主流语言”如C/C++、Java等传统的编程语言当然不想丧失这个生存权,分别以不同的方式来适应未来的并行计算的挑战。如C/C++,除了标准委员会致力于以标准的并行化库来支持并行计算,标准化的OPENMP和MPI。以及Intel的Threading Building Blocks库也都为并行计算提供了可靠的优雅的解决方案;Java在其的5.0版本引入了意义重大的concurrency库,来支持Java的并行化,获得了Java社区的追捧;而微软更是采用了多种技术手段来应对并行计算时代的到来:先是在.Net里面引入了APM(Asynchronous Programming Model),随后又在Robotics Studio中提供了CCR(Concurrency and Coordination Runtime)库,后来还发布了Parallel FX和MPI.Net。目前的主流的语言,虽然现在提供了对并行化的支持,但都是后来的拓展,原来的架构还是不支持并行化计算,强加的并行化支持打乱的人们以前的使用习惯。但是有一门语言,在诞生之初就支持并行化程序设计¾Erlang编程语言。
Erlang语言诞生很早,大概与Perl语言同岁,比C++年轻四岁,长Java十多岁。之前因为计算的串行化,虽然Erlang存在但是没有流行起来。但是随着并行计算的出现与发展,Erlang在并行化环境下,其优秀的并行化计算才真正体现了出来,引起了人们的注意,才逐渐为人们所熟知。
Erlang得名于丹麦数学家及统计学家Agner Krarup Erlang,同时Erlang还可以表示Ericsson Language。Erlang并非一门新语言,它出现于1987年,只是当时对并发、分布式需求还没有今天这么普遍,当时可谓英雄无用武之地。Erlang语言创始人Joe Armstrong当年在爱立信做电话网络方面的开发,他使用Smalltalk,可惜那个时候Smalltalk太慢,不能满足电话网络的高性能要求。但Joe实在喜欢Smalltalk,于是定购了一台Tektronix Smalltalk机器。但机器要两个月时间才到,Joe在等待中百无聊赖,就开始使用Prolog,结果等Tektronix到来的时候,他已经对Prolog更感兴趣,Joe当然不满足于精通Prolog,经过一段时间的试验,Joe给Prolog加上了并发处理和错误恢复,于是Erlang就诞生了。1987年Erlang测试版推出,并在用户实际应用中不断完善,于1991年向用户推出第一个版本,带有了编译器和图形接口等更多功能。1992年,Erlang迎来更多用户,如RACE项目等。同期Erlang被移植到VxWorks、PC和 Macintosh等多种平台,两个使用Erlang的产品项目也开始启动。1993爱立信公司内部独立的组织开始维护和支持Erlang实现和Erlang工具。
Erlang是一种通用的面向并发的编程语言,它由瑞典电信设备制造商爱立信所辖的CS-Lab开发,目的是创造一种可以应对大规模并发活动的编程语言和运行环境。Erlang问世于1987年,经过十年的发展,于1998年发布开源版本。Erlang是运行于虚拟机的解释性语言,但是现在也包含有乌普萨拉大学高性能Erlang计划(HiPE)开发的本地代码编译器,自R11B-4版本开始,Erlang也开始支持脚本式解释器。在编程范型上,Erlang属于多重范型编程语言,涵盖函数式、并发式及分布式。顺序执行的Erlang是一个及早求值, 单次赋值和动态类型的函数式编程语言。
Erlang是一个结构化,动态类型编程语言,内建并行计算支持。最初是由爱立信专门为通信应用设计的,比如控制交换机或者变换协议等,因此非常适合于构建分布式,实时软并行计算系统。使用Erlang编写出的应用运行时通常由成千上万个轻量级进程组成,并通过消息传递相互通讯。进程间上下文切换对于Erlang来说仅仅只是一两个环节,比起C/C++程序的线程切换要高效得多得多了。
Erlang具有并发性、分布式、健壮性、软实时性、热代码升级、递增式代码装载、快速准确暴露错误、面向并发性编程、函数式编程等特点。这些特点都会在Erlang的应用中有很好的体现。
Erlang是一种函数式编程语言。函数式编程是一种编程范型,它将计算机的运行视为函数的计算,避免了变量与状态的概念。我们常用的C/C++、Java等是指令语言。
Erlang的运行环境可以是基本的shell或编辑成erl文件然后编译运行。以下对两种基本的方式进行说明。这里假设你已经安装好Erlang运行环境。
A. Shell下运行Erlang代码
打开shell,输入erl & enter进入Erlang的shell运行环境,如图2-1。
图2-1 进入Erlang的运行环境
可以看到,我使用的Erlang的版本是17.退出可以用键盘组合按键^G退出shell的Erlang运行环境。
1>表示目前的运行环境是准备就绪,可以输入代码运行了。前面的数字会随着输入代码的成功运行的数目的增加而递增的。如图2-2展示的那样,先输入错误的代码:hello world.,其会提示错误后继续准备接受输入,但是前面的数字并没有发生变化,接着,输入可以接受的“hello world”.,则输出“hello world”,同时前面的数字加1,变成2。
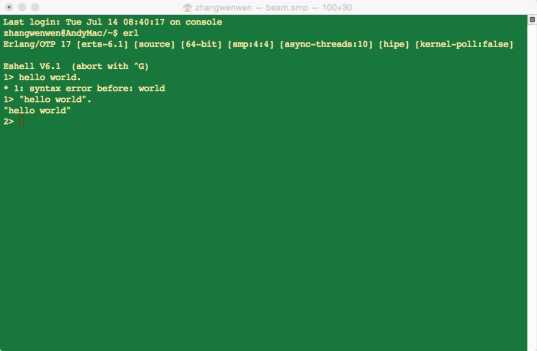
图2-2 基本的输入演示
在输入的时候,要注意在每个语句的后面都有一个小圆点(.),是不能省略的,不然的话,控制台就会继续等待输入,详细的会在后面介绍。
B. Erlang源代码文件的执行
Erlang源代码的文件后缀为.erl,每个文件就是一个模块。hello.erl实例代码如下:
-module(hello).
-export([hello_world/0]).
hello_world()->
io:format("Hello world~n").
进入Erlang运行环境进行编译,返回{ok,hello}则编译通过。并运行hello:hello_world().则输出Hello world,如图2-3所示。
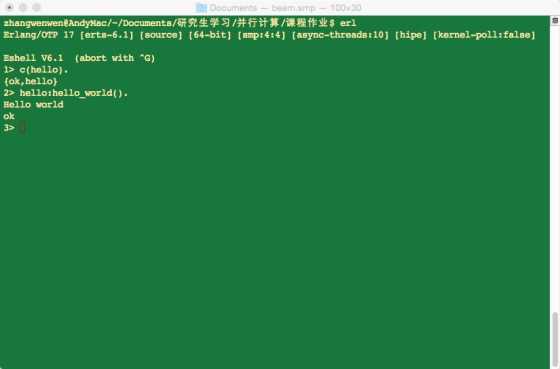
图2-3 模块编译与运行
以上就是两种运行Erlang代码的方式,在后面的实验中,会采用以上的其中的一种。为了避免后面的过多的截图,在这里约定,输入与输出按照如下的方式来表示,输入和输出的内容用斜体来表示,且前面以加粗的输入/输出来加以提醒。以运行hello_world()为例:
输入:输入的代码
输出:输出的运行结果
输入:hello:hello_world().
输出:hello world
ok
在Erlang中,变量的首字母都是大写的,且变量是一次性“赋值”,不可改变的。在大多数的语言中,=表示的是变量赋值,但是在Erlang中=表示的是模式匹配。在Erlang中,Lhs=Rhs的真正的意思是:先计算Rhs的值,然后将Rhs的值与Lhs进行匹配。
变量(比如X)是模式的一种简单的形式。X在第一次执行X=SomeExpression的时候,Erlang会对自己说,我要做些什么才能使这句话真?因为X还没有值,它可以绑定SomeExpression在X上,这条语句就成立了。然后,我们再执行X=AnotherExpression的时候,Erlang就会将AnotherExpression的值与SomeExpression的值进行匹配,若相同则成功;否则,失败。如下例:
输入:X=23. 输出:23
输入:X=43. 输出:** exception error: no match of right hand side value 43
上述例子中,先输入X=23.则第一次匹配成功;再输入X=43.的时候就会报匹配失败的错误。
Erlang的数据类型有数值(整数和浮点数)、二进制串/位串、原子、元组、列表(和字符串)、唯一标识符(端口,pid,引用)、Fun函数。
A. 数值
Erlang的数值有整数和浮点数。Erlang的整数没有大小的限制,较小的数字会被放置在单个机器字里面,较大的数字是按需分配的,对程序员是透明的。Erlang的浮点数采用的是IEEE 745-1985格式(双精度),其语法与大部分的编程语言是相同的,但是Erlang要求必须以数字开头。
Erlang的数值运算也有+、-、*、/等,其操作与一般的是操作的顺序和意义是相同的,在这里不再赘述。
B. 二进制串/位串
在Erlang中,二进制串是无符号8位字节的序列,用于存放和处理数据块。位串是广义的二进制串,其长度不必是8的整数倍,如3/2个字节的长度是12位。
二进制串的基本的语法如下:
<<0,1,2,3,4,…,255>>
也就是一个包含在<<…>>内的逗号分隔的整数序列,整数的取值范围是0~255。两边的分隔符是两个连续的小于号(大于号)。当然,我们还可以用字符串来构建二进制串,如:
<<”hello”,”zhangwenwen”>>
只要字符串里面的字符的编码是ASCII/Latin-1编码的,其取值在0~255之间就OK。
位串的基本的语法是:
<<Segment1,Segment2,…,SegmentN>>
其中,SegmentN可以是以下方式的中的一种:
Data
Data:Size
Data/TypeSpecifiers
Data:Size/TypeSpecifiers
在以上的模式中,Data指的是实际的数据,Size指的是位串的大小,TypeSpecifiers指的是位串的一些解码的细节,如大小端等的定义。
C. 原子
在Erlang中,原子是一种仅由字符序列来标识的特殊字符串常量,因此两个原子只要具有相同的字符串表示,就完全等同。
通常情况下,原子以小写字母开头,如hello,world等都是原子,在开头字母之后可以使用大写字母,@,#等其他的字符,但是为了在其他的情况下引起歧义,可能在定义的时候要引入单引号定义,如:
‘this is an atom’
若不加入单引号就会报错。
原子就像是Java或C语言中的enum类型,你可以在任何地方使用,且不需要事先定义。
D. 元组
元组是Erlang中的定长序列。元组用大括号来定义,如:
{1,2,3}
{one,two,three,four}
{}
元组的元素数目可以是0、1或多个。
E. 列表(和字符串)
列表是Erlang各种数据结构中的主力军---这点在大部分函数式编程语言都相通的。这是因为列表简单、高效、灵活和天然遵循引用透明性。
以[]来定义列表,如下:
[]
[1,2,3]
[“about”,”boy”,”cow”,”dog”]
还有一种特殊的列表就是字符串,在Erlang中,用双引号来定义,与其他的编程语言类似:
“hello world“
与
[104,101,108,108,111,32,119,111,114,108,100]
等价,也可以写成
[$h,$e,$l,$l,$o,$\ ,$w,$o,$r,$l,$d]。
F. 唯一标识符(端口,pid,引用)
Erlang支持进程编程,任何代码都需要一个Erlang进程作为载体才能执行。每个进程都有一个唯一的标识符,通常称为pid。Pid是一种特殊的Erlang数据类型,应被视为一种不透明对象,但shell会以<0.35.0>这样的格式来打印一个pid。在shell中你不能用这个语法来创建pid,该格式仅用于调试目的,方便对pid的比较。
端口标识符:端口和进程差不多,只是还能与外部通信。Shell打印端口的格式是#Port<0.472>.
在Erlang中可以用make_ref()来生成,其shell的输出格式为#Ref<0.0.0.39>
G. Fun函数
Erlang被称为函数式语言,这类语言的一个显著的特征就是可以像处理数据一样处理函数---也就是说,函数式可以称为其他函数的输入,也可以称为其他函数求值结果,还可以把函数存储在数据结构中供后续的使用。在Erlang中,将函数包装成数据的函数叫做Fun函数。
在Erlang中,对标点符号的使用与主流的编程语言是有差别的,在Erlang中使用标点符号的方式更像是在我们日常生活中交流语言所使用的标点符号的习惯。
在Erlang中,语句的结束用”.”而不是一般的编程语言中的”;”,”;”表示的是语句的短暂的停顿,如果是一系列语句,这些语句之间表示的是一种“或”的关系;而在Erlang中,”,”表示的是一种“且”的关系。
在Erlang中,语句块有:if、case、try…catch.
If语句的一般格式是:
if Guard1 –> Expr_seq2; Guard2->Expr_seq2; … end.
其中,Guard在Erlang中指的是条件判断语句。
Case语句的一般格式:
case Expression of Pattern1 –>Expr_seq1; Pattern->Expr_seq2; … end.
Case语句与一般的编程语言的原理是一样的,只不过是换了不同的表达格式而已。
Try…catch语句主要是为了抓取语言的异常信息,一般的格式如下:
try FunOrExpressionSeq of Pattern1 ->Expressions1; Pattern1 ->Expressions1; … catch ExceptionType1:ExPattern1->ExExpressions; ExceptionType1:ExPattern1->ExExpressions; … after AfterExpressions end.
与java的try…catch的结构类似:
try {
…
} catch (Exception e) {
…
} finally {
// TODO: handle finally clause
…
}
after与final等价。
在Erlang中没有for语句,但是我们可以用列表来模拟for语句达到的效果。
在Erlang中,函数是最基本的功能单元,其定义也是很简单的。如两个数相加sum(A,B)的定义如下:
sum(A,B) ->A+B.
Erlang的函数没有像其他语言那样有明确的返回值,但是每一个都会有一个返回值,为最后一个表达式的计算的值。在Erlang中,函数的函数名和函数主体的分隔符为 –>.
在Erlang中,存放代码的地方是模块(module)。Module相当于java语言中的类,是一系列方法的集合,下面是一个基本的模块的定义格式:
%% @author zhangwenwen %% @doc @todo Add description to demo. -module(demo). %% =================================================== %% API functions %% =================================================== -export([funcdemo/1,max/2]). %% =================================================== %% Internal functions %% =================================================== f(A,B) ->A+B. funcdemo(Test) ->Test. max(A,B) when A>=B ->A; max(A,B) when A<B ->B.
在上述代码中
%(%%)表示为Erlang的注释,在Erlang中没有块注释,只有行注释,以%开头;
-module指的是该模块的名称,与模块的文件名相同;
-export指的是可以在外部访问的API,导出的是一个列表,元素的格式是 函数名/参数的个数;
module文件的本体是相关API的实现。
注意:在模块源文件中,-module和-export前面还有字符‘-’,初学者应该在编写模块的时候注意,比较容易忽略。
以上内容简单介绍了Erlang编程语言的顺序编程的基本的概念和数据结构,详细的语法规则请参考相关Erlang编程书籍。
从Erlang的发展的历史我们知道,Erlang在很早就出现了,但是其并不是被大多数人知道,尽管它还是开源的。但是,近年来,随着并行化硬件的发展,Erlang的得天独厚的特点使得其逐渐被人们所了解。
可见,Erlang在并行化编程方面有很大的优势和很好的应用前景。在本节,就是对Erlang的并行编程的进行相关的介绍。
在我们生活的这个世界是并行的,我们参与的一切活动都是并行的,我们的大脑对并行也有着深刻的理解。大脑里有一个称为“杏仁核”的区域让我们对刺激做出迅速的反应。我们在高速路上开汽车的时候,有了需要踩下刹车的想法的时候我们已经踩下了刹车。如果我们首先是想应该踩下刹车,然后再去执行的话,我们多半已经躺在了医院里或者是蹲在了交警大队里了。
并行可以提高资源的利用率,可以节省一件工作的工作时间。我们一直在强调团队的合作的重要性,就是因为在一个团队里面,一个工作被分配给不同的个体,各个个体之间进行并行完成,缩短了工作的时间间距。如果所有的这些工作都是由一个人来完成,那么工作的时间间距将大大增加。并行是必要的,是提高工作效率很好的方式。
在计算机世界里,并行同样重要。通过并行化完成任务来完成任务来节省时间是目前最新的计算发展趋势。以前,在特定的时间完成特定计算的不可能通过对并行的引入已经变成了可能。
Erlang的并行是基于进程的。进程是一些独立的小型的虚拟机,可以执行Erlang函数。Erlang的进程隶属于编程语言,而不是操作系统。这就意味着,Erlang的进程在任何操作系统上都具有相同的逻辑行为,我们就可以编写可移植的并发代码。Erlang的进程与进程之间是独立的个体,不进行内存共享,而是通过消息传递来传递数据。Erlang进行不共享内存,在使用内存的时候就不存在内存锁来防止冲突。一个Erlang程序可能有几十个、几百个甚至几十万个小的进程。所有的这些进程都是独立运作的。每个进程都有一块独立的内存区域。它们表现的就像是在一个很大的房子一大群喋喋不休。
这样就使得Erlang程序天生易于管理和扩展。假如我们有10个这样的进程,而它们有太多的工作要做,我们怎么办?当然是找更多的进程过来。那么,如何管理这些进程呢?很简单,就是大声将消息广播给它们就可以了。
利用Erlang进行并行化编程是十分简单的。要想编写并行的Erlang的程序,只需要三个新的基本的函数:spawn、send和receive。spawn函数创建一个并行进程,返回一个我们在前面提到的数据类型pid;send向某个进程发送消息;receive则是接收消息。
spawn函数的使用格式:
Pid=spwan(Mod,Func,Args).
创建新的并发进程来执行Mod:Func(Args)。这个新创建进程和调用进程并列运行。spawn返回一个Pid,process identifier的简称,即进程标识符。可以使用Pid来给此进程发送消息。
在模块内部可以直接使用Pid=spawn(Func)来创建一个并行的进程,Func可以不导出。这种形式的spawn总是被执行Func的最新值。
Pid!Message:向标识符为Pid的进程发送消息Message。消息发送是异步的,发送方并不等待,而是会继续之前的工作。!被称为发送操作符。Pid!M的值被定义为M,Pid1!Pid2!Pid3!…!Pidn!M,因为是从后往前计算,前面的表达式就是将消息M发送给所有的进程Pid1、Pid2、…、Pidn。
receive … end,接收某个进程发送来的消息,它的语法如下:
receive Pattern1 ->Expressions1; Pattern2 ->Expressions2; … end
当某个消息达到时,系统会尝试将收到的消息与Pattern进行匹配,若匹配成功,就执行后面的表达式;如果匹配不成功,就匹配后面的pattern…。如果没有匹配成功的模式就会将消息保存起来后面来进行处理。
下面以一个简单的计算面积的实例来对以上的函数进行简单的使用。模块的文件名称是area_server0.erl,具体的代码如下:
%%模块的定义
-module(area_server0).
%%导出的API,在外部可以进行访问
-export([loop/0]).
%%循环接收消息的函数
loop() ->
receive
{rectangle,Width,Height} ->
io:format("Area of rectangle is ~p~n",[Width*Height]),
loop();
{square,Side} ->
io:format("Area of square is ~p~n",[Side*Side]),
loop();
{circle,Radus} ->
io:format("Arae of circle is ~p~n",[3.14159*Radus*Radus]),
loop()
end.
编译并在shell中输入运行如图3-1:
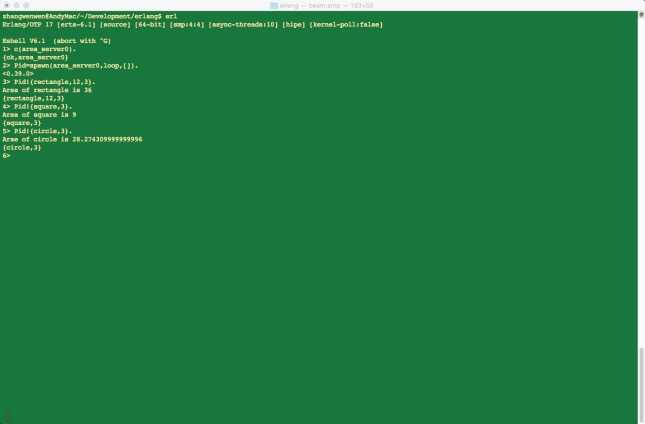
图3-1 进程创建以及消息发送
可以在以上的基础上,对代码进行进一步的包装,将spawn函数完全封装在模块的一个函数里面,实现全面的封装,将消息发送也封装在模块中。通过以上的实践,我们可以知道,Erlang确实是可以很好地进行并行编程。
之所以并行计算在这几年发展迅速,是因为其并发可以很好很好实现计算的加速。在本节中,通过实验说明并行计算确实是可以提升计算的速度,减少计算的时间;同时也是为了验证Erlang的并行编程的实际应用的能力。
利用串行与并行的方式进行大矩阵的乘法并比较这两种情况下运行的时间,并与理论运行时间值作出比较,得出结论。
本实验的目的是为了验证串行的矩阵乘法与并行的矩阵乘法的运行时间的比较,比较的前提是矩阵的大小是相同的。目前,假设有矩阵AM*N和矩阵BN*Q,相乘的结果是CM*Q。
串行的数据矩阵乘积采用的是传统的矩阵相乘的算法:
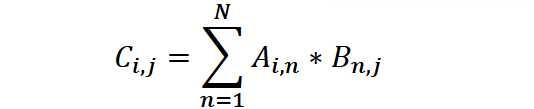
结果C的每一项是对应的A与B的行与列的乘积的和。
而并行计算的矩阵乘积这里采用的是将矩阵A的每一行发送给每一个进程与矩阵B相乘,得到结果C的相应的行列。
实验的环境:操作系统 Windows 7 旗舰版 Erlang/OPT版本:18.0
硬件设施:CPU:Intel(R) Core(TM)i5 CPU M480 @2.67GHz
内存:8GB 内存
A. 随机生成矩阵M*N的矩阵,在实验中为了方便,仅仅生成的是M*M的方阵,生成方阵的代码如下:
generateMatrix(M,N) -> row(M,N,[]). row(M,N,Result) -> case 0=:=M of true ->Result; false->row(M-1,N,Result++[column(N,[])]) end. column(N,Result) -> case 0=:=N of true ->Result; false->column(N-1,Result++[random:uniform(10)]) end.
B. 分别进行串行与并行计算矩阵A与矩阵B的乘积,相关的代码如下:
串行计算的相关的代码:
singleProcess(A,B)-> _R=lists:foldl(fun(Row_A,Acc)->Acc++[rowMultiplymatrix(Row_A,B,1,[])]end, [], A).
并行计算的相关的代码:
multiProcess(A,B) ->
P=self(),
lists:foldl(fun(A_Row,_Acc)-> spawn(fun()->P!{self(),rowMultiplymatrix(A_Row,B,1,[])} end) end, [], A),
receiveMessage(length(A),[]).
其他相关的调用的代码:
rowMultiplymatrix(Row_A,Matrix_B,Count_Col,Result)->
case Count_Col=:=length(lists:nth(1, Matrix_B))+1 of
true ->Result;
false ->rowMultiplymatrix(Row_A,Matrix_B,Count_Col+1,Result++[multiply(Row_A,getColume(Matrix_B,Count_Col),0)])
end.
receiveMessage(Count,Result) ->
receive
{_Pid,_Result}->
case Count=:=1 of
true ->Result++[_Result];
false ->
receiveMessage(Count-1,Result++[_Result])
end
end.
C. 首先用较小的矩阵来验证代码的正确性
1. 生成4*4的矩阵A和矩阵B,生成的结果如下:
生成的矩阵A的数据如下:
[[1,8,4,9],[9,8,2,4],[3,7,4,5],[7,2,8,9]]
生成的矩阵B的数据如下:
[[3,9,9,6],[9,6,3,10],[10,8,1,3],[9,3,4,9]]
2. 将矩阵A和矩阵B分别按照串行并并行的方式来计算得到矩阵C。
串行计算的矩阵乘积如下:
["ÄtI³",[155,157,123,176],[157,116,72,145],"Ȧq§"]
并行计算的矩阵乘积如下:
["ÄtI³",[155,157,123,176],[157,116,72,145],"Ȧq§"]
在上面的结过中,我们发现有“ÄtI³”、“Ȧq§”等可见的字符,这是正确的。在前面我们已经提到过,Erlang中的字符串是特殊的列表,且如果这些字符都是可见的,则Erlang就将这些列表显示为可见的字符串,所以以上的结果就是可见字符对应的ASCII码。经过手工计算,可以发现,串行和并行的计算的结果都是正确的。
D. 分别生成100*100、200*200、…、500*500的矩阵进行计算,记录其计算的时间,其中计算串行的执行时间和并行的执行时间的代码分别如下:
计算串行执行的时间的代码:
test_p(A,B) -> Start=milliseconds(), singleProcess(A,B), End=milliseconds(), End-Start.
计算并行的执行时间的代码:
test_m(A,B) -> Start=milliseconds(), multiProcess(A,B), End=milliseconds(), End-Start.
其中得到当前时间的微秒数的函数代码如下:
milliseconds()->
{Megaseconds,Seconds,Milliseconds}=erlang:timestamp(),
Megaseconds*1000000000000+Seconds*1000000+Milliseconds.
分别记录不同的大小的方阵的乘积的时间如下表:
表4-1 不同矩阵大小的串并行计算时间
|
矩阵大小 |
100*100 |
200*200 |
300*300 |
400*400 |
500*500 |
|
串时间/μs |
3961984 |
45411822 |
196529231 |
887329534 |
2012385931 |
|
并时间/μs |
1574994 |
21824914 |
121664524 |
374340732 |
1019530991 |
完整的代码见附录。
由以上的实验,可以明显看到,相同的计算量,并行方式下的计算时间明显小于串行方式下的计算时间,更直观的对比如图4-1:
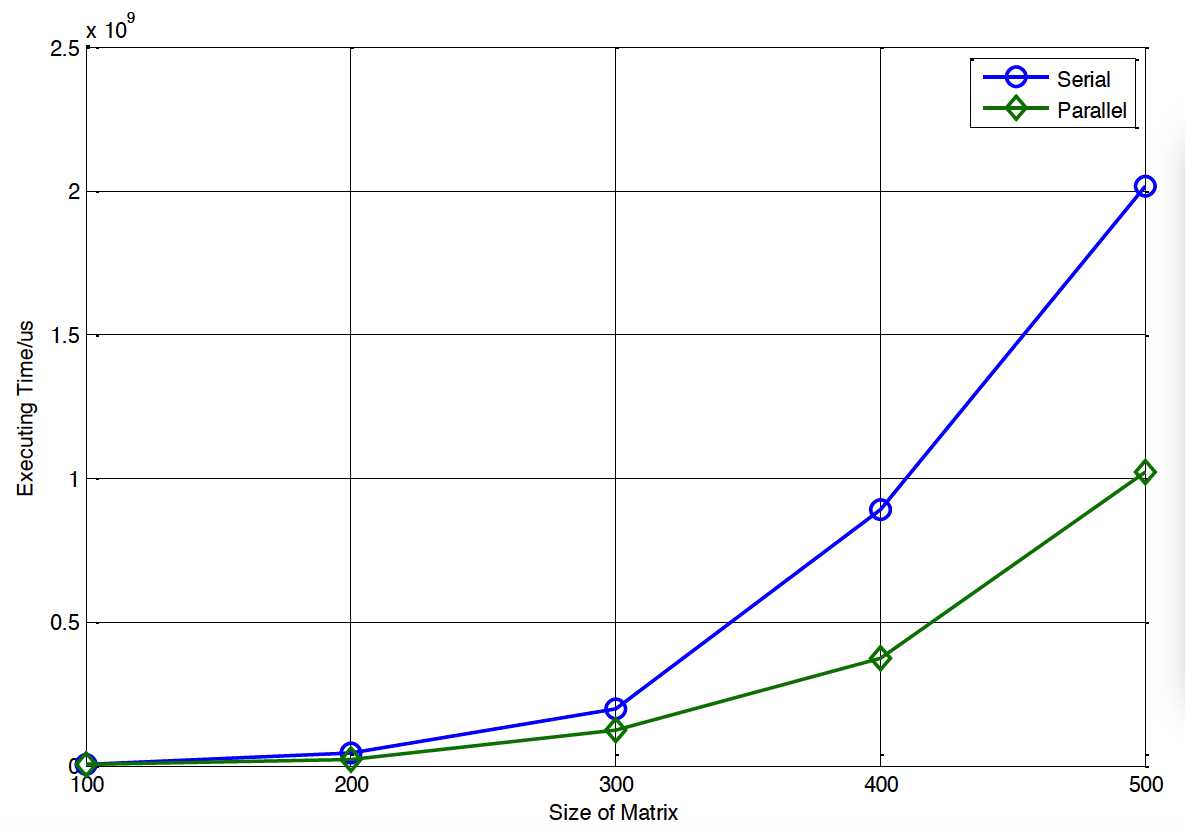
图4-1 并行与串行计算时间的比较
并行计算之所以能够在较短的时间内完成对矩阵的计算,主要是其对并行计算资源的充分利用从而达到减少执行时间的目的。这点可以从程序在执行不同的方式的CPU的利用率可以看出。
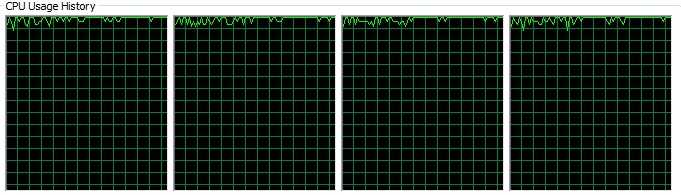
图4-2 并行计算时CPU的利用率
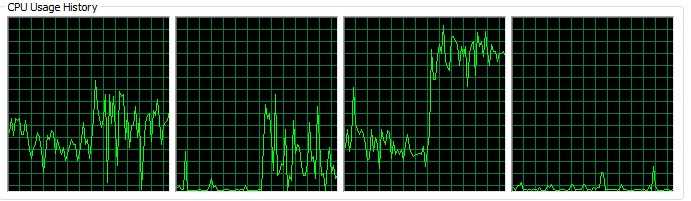
图4-3 串行计算时CPU的利用率
从以上的两图可以看出,并行计算下的CPU的使用率远远大于串行计算的CPU的使用率。并行计算中,CPU的资源被充分利用,这也体现了Erlang的优秀的并行编程的特性:将所有的进程分配给所有的CPU,使得所有的计算资源都充分利用。
Erlang编程语言对并行化的支持是良好的。通过这段时间对Erlang语言的学习研究,不仅了解了更多的关于编程语言的知识,掌握了一门编程语言,了解了一种编程范式;同时,对并行计算有了更加深刻的认识。在学习了基本的理论的同时,将相关的理论应用在了实践中---矩阵乘积的并行计算与串行计算的比较,可以知道,并行的技术确实在并行的硬件的环境下,相比串行计算,节省一半多的时间。但是,目前知道的仅仅是皮毛,在本文中也有很多的瑕疵,需要学习的还很多,希望在将来将学习到的知道多应用,同时也希望看到本文的各位不吝赐教。
附录
实验相关的完整代码如下:
%% @author Andy %% @doc @todo Add description to demo.
-module(demo). %% ==================================================== %% API functions %% ==================================================== -export([]). -compile(export_all). %% ==================================================== %% Internal functions %% ====================================================
%%随机生成M*N的矩阵 generateMatrix(M,N) -> row(M,N,[]). row(M,N,Result) -> case 0=:=M of true ->Result; false->row(M-1,N,Result++[column(N,[])]) end. column(N,Result) -> case 0=:=N of true ->Result; false->column(N-1,Result++[random:uniform(10)]) end. %%A矩阵的行与矩阵B相乘得到新的行 rowMultiplymatrix(Row_A,Matrix_B,Count_Col,Result)-> case Count_Col=:=length(lists:nth(1, Matrix_B))+1 of true ->Result; false ->rowMultiplymatrix(Row_A,Matrix_B,Count_Col+1,Result++[multiply(Row_A,getColume(Matrix_B,Count_Col),0)]) end. multiply([H1|T1],[H2|T2],Sum) when length(T1)=:=length(T2) -> multiply(T1,T2,Sum+H1*H2); multiply([],[],Sum)->Sum. %%得到矩阵M的Col列 getColume(M,Col) -> lists:foldl(fun(A,Acc)->Acc++[lists:nth(Col, A)] end, [], M). %%串行的矩阵相乘 singleProcess(A,B)-> _R=lists:foldl(fun(Row_A,Acc)->Acc++[rowMultiplymatrix(Row_A,B,1,[])]end, [], A). %%并行的矩阵相乘 multiProcess(A,B) -> P=self(), lists:foldl(fun(A_Row,_Acc)-> spawn(fun()->P!{self(),rowMultiplymatrix(A_Row,B,1,[])} end) end, [], A), receiveMessage(length(A),[]). %%循环接收计算的结果 receiveMessage(Count,Result) -> receive {_Pid,_Result}-> case Count=:=1 of true ->Result++[_Result]; false -> receiveMessage(Count-1,Result++[_Result]) end end. %%得到当前时间的微秒数 milliseconds()-> {Megaseconds,Seconds,Milliseconds}=erlang:timestamp(), Megaseconds*1000000000000+Seconds*1000000+Milliseconds. %%并行矩阵相乘的时间计算 test_m(A,B) -> Start=milliseconds(), multiProcess(A,B), End=milliseconds(), End-Start. %%串行的矩阵相乘的时间计算 test_p(A,B) -> Start=milliseconds(), singleProcess(A,B), End=milliseconds(), End-Start.
标签:
原文地址:http://www.cnblogs.com/Andy-wen/p/4834851.html