标签:
动态规划和贪心算法都是一种递推算法 即均由局部最优解来推导全局最优解 (不从整体最优解出发来考虑,总是做出在当前看来最好的选择。)
不同点:
贪心算法
与动态规划的区别:贪心算法中,作出的每步贪心决策都无法改变,由上一步的最优解推导下一步的最优解,所以上一部之前的最优解则不作保留。
能使用贪心法求解的条件:是否能找出一个贪心标准。我们看一个找币的例子,如果一个货币系统有三种币值,面值分别为一角、五分和一分,求最小找币数时,可以用贪心法求解;如果将这三种币值改为一角一分、五分和一分,就不能使用贪心法求解。
例:贪心法标准的选择
设有n个正整数,将它们连接成一排,组成一个最大的多位整数。
例如:n=3时,3个整数13,312,343,连成的最大整数为34331213。
又如:n=4时,4个整数7,13,4,246,连成的最大整数为7424613。
输入:n个数
输出:连成的多位数
算法分析:此题很容易想到使用贪心法,在考试时有很多同学把整数按从大到小的顺序连接起来,测试题目的例子也都符合,但最后测试的结果却不全对。按这种标 准,我们很容易找到反例:12,121应该组成12121而非12112,那么是不是相互包含的时候就从小到大呢?也不一定,如12,123就是 12312而非12123,这种情况就有很多种了。是不是此题不能用贪心法呢?其实此题可以用贪心法来求解,只是刚才的标准不对,正确的标准是:先把整数转换成字符串,然后在比较a+b和b+a,如果a+b>=b+a,就把a排在b的前面,反之则把a排在b的后面。
动态规划算法
与贪心法的区别:不是由上一步的最优解直接推导下一步的最优解,所以需要记录上一步的所有解 (下例中的F[i][j]就表示第i行的j个解)
能使用动态规划算法的条件:
如果一个问题被划分各个阶段之后,阶段I中的状态只能由阶段I-1中的状态通过状态转移方程得来,与其它状态没有关系,特别是与未发生的状态没有关系,那么这个问题就是“无后效性”的,可以用动态规划算法求解
动态规划算法求解:
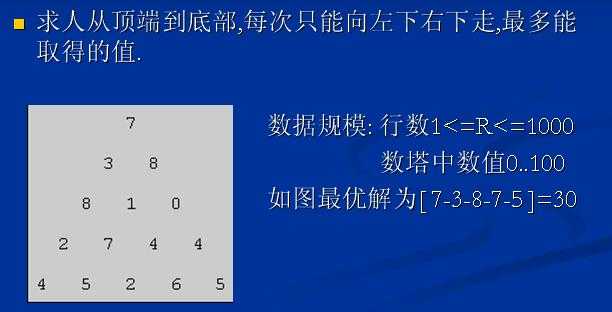
1。定义阶段:第i行第j列的值a[i][j]
2。定义状态:走到第i行第j列的最大值F[i][j]
3。状态转移方程:F[i][j] = a[i][j]+max(F[i+1][j], F[i+1][j+1])
4。定义边界条件:当i = n时,F[i][j] = a[i][j]; 即一开始可以直接得出的局部最优解
贪心算法和动态规划算法
标签:
原文地址:http://www.cnblogs.com/qionglouyuyu/p/4843475.html
