标签:
本节讲解如何预测患者需要佩戴的隐形眼镜类型。
1、使用决策树预测隐形眼镜类型的一般流程
(1)收集数据:提供的文本文件(数据来源于UCI数据库)
(2)准备数据:解析tab键分隔的数据行
(3)分析数据:快速检查数据,确保正确地解析数据内容,使用createPlot()函数绘制最终的树形图
(4)训练算法:createTree()函数
(5)测试算法:编写测试函数验证决策树可以正确分类给定的数据实例
(6)使用算法:存储数的数据结构,以使下次使用时无需重新构造树
trees.py如下:
#!/usr/bin/python
# -*- coding: utf-8 -*-
from math import log
#计算给定数据集的香农熵
def calcShannonEnt(dataSet):
numEntries=len(dataSet)
labelCounts={}
for featVec in dataSet:
currentLabel=featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1
shannonEnt=0.0
for key in labelCounts:
prob=float(labelCounts[key])/numEntries
shannonEnt -=prob*log(prob,2)
return shannonEnt
#按照给定特征划分数据集
def splitDataSet(dataSet,axis,value):
retDataSet=[]
for featVec in dataSet:
if featVec[axis]==value:
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
#选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
numFeatures=len(dataSet[0])-1
baseEntropy=calcShannonEnt(dataSet) #计算整个数据集的原始香农熵
bestInfoGain=0.0;bestFeature=-1
for i in range(numFeatures): #循环遍历数据集中的所有特征
featList=[example[i] for example in dataSet]
uniqueVals=set(featList)
newEntropy=0.0
for value in uniqueVals:
subDataSet=splitDataSet(dataSet,i,value)
prob=len(subDataSet)/float(len(dataSet))
newEntropy+=prob*calcShannonEnt(subDataSet)
infoGain=baseEntropy-newEntropy
if(infoGain>bestInfoGain):
bestInfoGain=infoGain
bestFeature=i
return bestFeature
def majorityCnt(classList):
classCount={}
for vote in classList:
if vote not in classCount.keys():classCount[vote]=0
classCount[vote]+=1
sortedClassCount=sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
#创建树的函数代码
def createTree(dataSet,labels):
classList=[example[-1] for example in dataSet]
if classList.count(classList[0])==len(classList): #类别完全相同规则停止继续划分
return classList[0]
if len(dataSet[0])==1: return majorityCnt(classList)
bestFeat=chooseBestFeatureToSplit(dataSet)
bestFeatLabel=labels[bestFeat]
myTree={bestFeatLabel:{}}
del(labels[bestFeat]) #得到列表包含的所有属性
featValues=[example[bestFeat] for example in dataSet]
uniqueVals=set(featValues)
for value in uniqueVals:
subLabels=labels[:]
myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
return myTree
#测试算法:使用决策树执行分类
def classify(inputTree,featLabels,testVec):
firstStr=inputTree.keys()[0]
secondDict=inputTree[firstStr]
featIndex=featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex]==key:
if type(secondDict[key]).__name__==‘dict‘:
classLabel=classify(secondDict[key],featLabels,testVec)
else:classLabel=secondDict[key]
return classLabel
#使用算法:决策树的存储
def storeTree(inputTree,filename):
import pickle
fw=open(filename,‘w‘)
pickle.dump(inputTree,fw)
fw.close()
def grabTree(filename):
import pickle
fr=open(filename)
return pickle.load(fr)
treePlotter.py如下:
#!/usr/bin/python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
from numpy import *
import operator
#定义文本框和箭头格式
decisionNode=dict(boxstyle="sawtooth",fc="0.8")
leafNode=dict(boxstyle="round4",fc="0.8")
arrow_args=dict(arrowstyle="<-")
#绘制箭头的注解
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
createPlot.ax1.annotate(nodeTxt,xy=parentPt,xycoords=‘axes fraction‘,xytext=centerPt,textcoords=‘axes fraction‘,va="center",ha="center",bbox=nodeType,arrowprops=arrow_args)
def createPlot():
fig=plt.figure(1,facecolor=‘white‘)
fig.clf()
createPlot.ax1=plt.subplot(111,frameon=False)
plotNode(U‘决策节点‘,(0.5,0.1),(0.1,0.5),decisionNode)
plotNode(U‘叶节点‘,(0.8,0.1),(0.3,0.8),leafNode)
plt.show()
#获取叶节点的数目和树的层数
def getNumLeafs(myTree):
numLeafs=0
firstStr=myTree.keys()[0]
secondDict=myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__==‘dict‘:
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs +=1
return numLeafs
def getTreeDepth(myTree):
maxDepth=0
firstStr=myTree.keys()[0]
secondDict=myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__==‘dict‘:
thisDepth=1+getTreeDepth(secondDict[key])
else:thisDepth=1
if thisDepth>maxDepth:maxDepth=thisDepth
return maxDepth
def retrieveTree(i):
listOfTrees=[{‘no surfacing‘:{0:‘no‘,1:{‘flippers‘:{0:‘no‘,1:‘yes‘}}}}, {‘no surfacing‘:{0:‘no‘,1:{‘flippers‘:{0:{‘head‘:{0:‘no‘,1:‘yes‘}},1:‘no‘}}}}]
return listOfTrees[i]
#在父节点间填充文本信息
def plotMidText(cntrPt,parentPt,txtString):
xMid=(parentPt[0]-cntrPt[0])/2.0+cntrPt[0]
yMid=(parentPt[1]-cntrPt[1])/2.0+cntrPt[1]
createPlot.ax1.text(xMid,yMid,txtString)
#计算宽和高
def plotTree(myTree,parentPt,nodeTxt):
numLeafs=getNumLeafs(myTree)
depth=getTreeDepth(myTree)
firstStr=myTree.keys()[0]
cntrPt=(plotTree.xOff+(1.0+float(numLeafs))/2.0/plotTree.totalW,plotTree.yOff)
plotMidText(cntrPt,parentPt,nodeTxt) #计算父节点和子节点的中间位置
plotNode(firstStr,cntrPt,parentPt,decisionNode)
secondDict=myTree[firstStr]
plotTree.yOff=plotTree.yOff-1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__==‘dict‘:
plotTree(secondDict[key],cntrPt,str(key))
else:
plotTree.xOff=plotTree.xOff+1.0/plotTree.totalW
plotNode(secondDict[key],(plotTree.xOff,plotTree.yOff),cntrPt,leafNode)
plotMidText((plotTree.xOff,plotTree.yOff),cntrPt,str(key))
plotTree.yOff=plotTree.yOff+1.0/plotTree.totalD
def createPlot(inTree):
fig=plt.figure(1,facecolor=‘white‘)
fig.clf()
axprops=dict(xticks=[],yticks=[])
createPlot.ax1=plt.subplot(111,frameon=False,**axprops)
plotTree.totalW=float(getNumLeafs(inTree))
plotTree.totalD=float(getTreeDepth(inTree))
plotTree.xOff=-0.5/plotTree.totalW;plotTree.yOff=1.0;
plotTree(inTree,(0.5,1.0),‘‘)
plt.show()
lenses.txt如下:
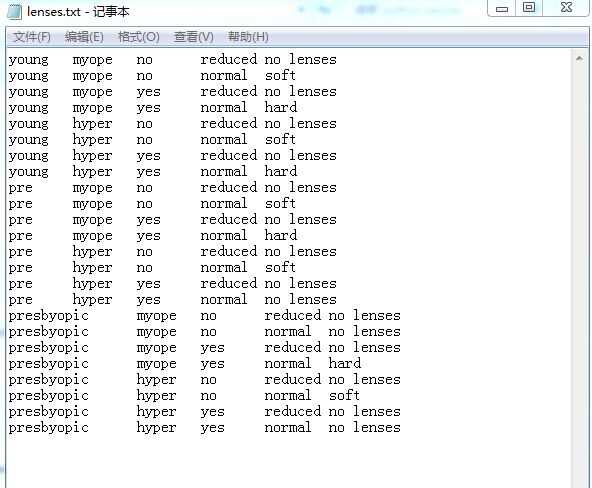
运行如下:
1 >>> import trees 2 >>> import treePlotter 3 >>> fr=open(‘lenses.txt‘) 4 >>> lenses=[inst.strip().split(‘\t‘) for inst in fr.readlines()] 5 >>> lensesLabels=[‘age‘,‘prescript‘,‘astigmatic‘,‘tearRate‘] 6 >>> lensesTree=trees.createTree(lenses,lensesLabels) 7 >>> lensesTree 8 {‘tearRate‘: {‘reduced‘: ‘no lenses‘, ‘normal‘: {‘astigmatic‘: {‘yes‘: {‘prescript‘: {‘hyper‘: {‘age‘: {‘pre‘: ‘no lenses‘, ‘presbyopic‘: ‘no lenses‘, ‘young‘: ‘hard‘}}, ‘myope‘: ‘hard‘}}, ‘no‘: {‘age‘: {‘pre‘: ‘soft‘, ‘presbyopic‘: {‘prescript‘: {‘hyper‘: ‘soft‘, ‘myope‘: ‘no lenses‘}}, ‘young‘: ‘soft‘}}}}}} 9 >>> treePlotter.createPlot(lensesTree)
由图看出决策树非常好地匹配了实验数据,然而这些匹配选项可能太多。我们将这种问题称之为过度匹配(overfitting)。为了减少过度匹配问题,我们可以裁剪决策树,去掉一些不必要的叶子节点。如果叶子节点只能增加少许信息,则可以删除该节点,将它并入到其他叶子节点中。
标签:
原文地址:http://www.cnblogs.com/chamie/p/4847546.html