标签:
(一)
仔细阅读示例: EnumTest.java,运行它,分析运行结果?
你能得到什么结论?你掌握了枚举类型的基本用法了吗?
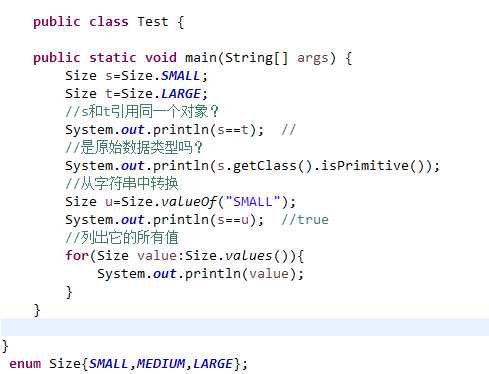
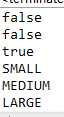
结论:枚举不属于原始数据类型,它的每个具体值都引用一个特定的对象。相同的值则引用同一个对象。
(二)
1. 原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
即
[-127 , 127]
原码是人脑最容易理解和计算的表示方式.
2. 反码
反码的表示方法是:
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变,其余各个位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.
3. 补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.
(三)
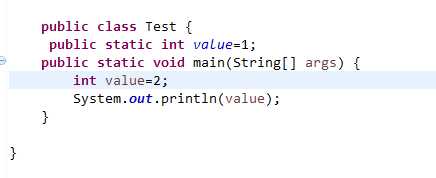

(四)
为什么double类型的数值进行运算得不到“数学上精确”的结果?
请通过互联网查找资料,或者是阅读相关计算机教材,解决这个问题。
这个涉及到二进制与十进制的转换问题。 N进制可以理解为:数值×基数的幂,例如我们熟悉的十进制数123.4=1×10²+2×10+3×(10的0次幂)+4×(10的-1次幂);其它进制的也是同理,例如二进制数11.01=1×2+1×(2的0次幂)+0+1×(2的-2次幂)=十进制的3.25。 double类型的数值占用64bit,即64个二进制数,除去最高位表示正负符号的位,在最低位上一定会与实际数据存在误差(除非实际数据恰好是2的n次方)。 举个例子来说,比如要用4bit来表示小数3.26,从高到低位依次对应2的1,0,-1,-2次幂,根据最上面的分析,应当在二进制数11.01(对应十进制的3.25)和11.10(对应十进制的3.5)之间选择。 简单来说就是我们给出的数值,在大多数情况下需要比64bit更多的位数才能准确表示出来(甚至是需要无穷多位),而double类型的数值只有64bit,后面舍去的位数一定会带来误差,无法得到“数学上精确”的结果。
n 注意:在构建BigDecimal对象时应使用字符串而不是double数值,否则,仍有可能引发计算精度问题。(为什么会这样呢?)
double,不能准确地代表16位有效数以上的数字,在使用BigDecimal时,应用 BigDecimal(String)构造器创建对象才有意义。另外,BigDecimal所创建的是对象,我们不能使用传统的+、-、*、/等算术运算 符直接对其对象进行数学运算,而必须调用其相对应的方法。方法中的参数也必须是BigDecimal的对象。
(五)
n 以下代码的输出结果是什么?
int X=100;
int Y=200;
System.out.println("X+Y="+X+Y);
System.out.println(X+Y+"=X+Y");
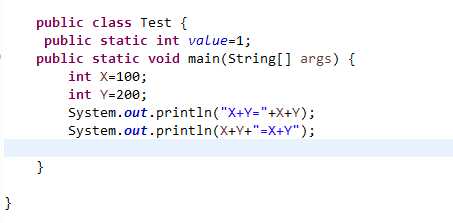
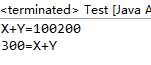
n 为什么会有这样的输出结果?
引号中输入什么就会在屏幕上输出什么,等号两边为数值时,等号为运算符,等号两边为非数值时,等号为连接符。
标签:
原文地址:http://www.cnblogs.com/jinpeigang/p/4859784.html