标签：
1.程序截图
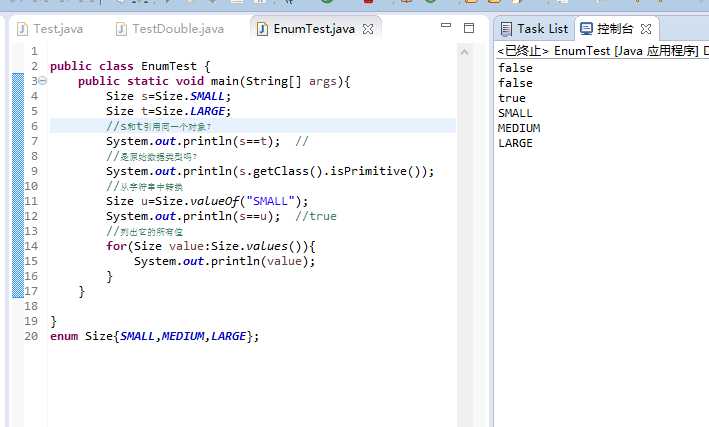
第一个false：判断s和t里的值，不同则输出false
第二个false：当且仅当这个类表示一个基本类型此方法返回true
第三个true：判断s和u里的值，相同则输出true
最后则是列出Size的所有值。
其中的问题：
//s和t引用同一个对象？不是
//是原始数据类型吗？不是
2.计算机的原码、补码和反码：
1.原码：原码表示法是机器数的一种简单的表示法。其符号位用 0表示正号，用1表示负号，数值一般用二进制形式表示。
2.补码：机器数的补码可由原码得到。如果机器数是正数，则该机器数的补码与原码一样；如果机器数是负数，则该机器数的补码是对它的原码（除符号位外）各位取反，并在未位加1而得到 的。
3.反码：机器数的反码可由原码得到。如果机器数是正数，则该机器数的反码与原码一样；如果机器数是负数，则该机器数的反码是对它的原码（符号位除外）各位取反而得到的。
例如：[X1] = +1010110（二进制）
[X1] 原= 01010110
[X1] 补= 01010110
[X1]反 = 01010110
[X2] = -1001010（二进制）
[X2]原 = 11001010
[X2] 补= 10110110
[X2] 反= 10110101
3.同名变量的屏蔽原则：
在一个方法内，可以定义和成员变量同名的局部变量或参数，此时成员变量被屏蔽。此时如果想要访问成员变量，可以通过 this关键字来访问，this关键字来访问，this 为当前实例的引用，如果要访问类变量，可以通过类名来访问。
×(10的-1次幂)；其它进制的也是同理，例如二进制数11.01=1×2+1×(2的0次幂)+0+1×(2的-2次幂)=十进制的3.25。5.以下代码的输出结果是什么？
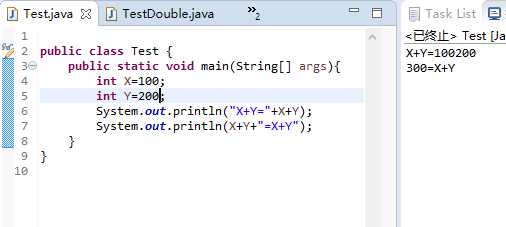
为什么会有这样的输出结果？
因为输出的是字符串，所以前一个分别输出两个字符串，而后一个表示用字符串输出两个整形的和。
标签：
原文地址：http://www.cnblogs.com/nxxam/p/4860009.html
