标签:
---恢复内容开始---
在看数据结构的串的讲解的时候,讲到了KMP算法——一个经典的字符串匹配的算法,具体背景自行百度之,是一个很牛的图灵奖得主和他的学生提出的。
一开始看算法的时候很困惑,但是算法思想很简单,就是在暴力匹配的基础上得出的。
暴力匹配
这里有必要说一下暴力匹配,暴力匹配更简单,就是按照人的常规思维去匹配字符串,拿模式串(P)的第一个字符去和给定串(S)比较,S从左往右看,一看,第一个,呀~不对,啥也不说了,第一个都不对了,后边还比个毛。所以,这一次比较,S中第一个字符开头是匹配串就不可能了。然后就拿P的第一个字符,去和S中第二个字符开头的比较,一看,对上了,有希望,再往后看,全对上了,恭喜你,程序结束了,没对上,也不要气馁,开始看S的第三个字符开头的字符串……如此一遍遍重复,直到找到匹配串。
上述算法暴力,简单,但复杂度高,O(n2)的,一次就找到算你幸运,但是,形如“0000000001”的串S和形如“000001”的匹配起来就麻烦了,每次移动一个,看到P串的最后一个才发现不行,直到P串移动到最后。
KMP
那么KMP就解决了这个问题,他让P串不是简单地往后移动一个了,而是移动k个,因为,我们每次比较时,前若干字符在上一次比较中的情况已经知道了,所以我们在下一次比较时,可以利用上一次比较的结果,不用再去做无用功了。
那么关键来了,他为什么可以移动k个呀,你怎么保证你在移动k个的时候(略过了移动0~k个),没有把正确答案错过?思前想后,个人觉得,归根结底还是根据模式串P的前缀和后缀的重复性决定的。
这里有两个问题要解释
(1)前缀和后缀
举个栗子,字符串“ababa” 的所有前缀为“a”、“ab”、“aba”、“abab”,就是以第一个字符开头,不包含最后一个字符的所有子串。同理,所有后缀就是“a”、“ba”、“aba”、“baba”,就是以最后一个字符结尾,不包含第一个字符的所有子串。
(2)重复性
关键来了,我觉得这是能使P向后移动k个而不是1个的基础。
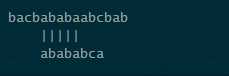
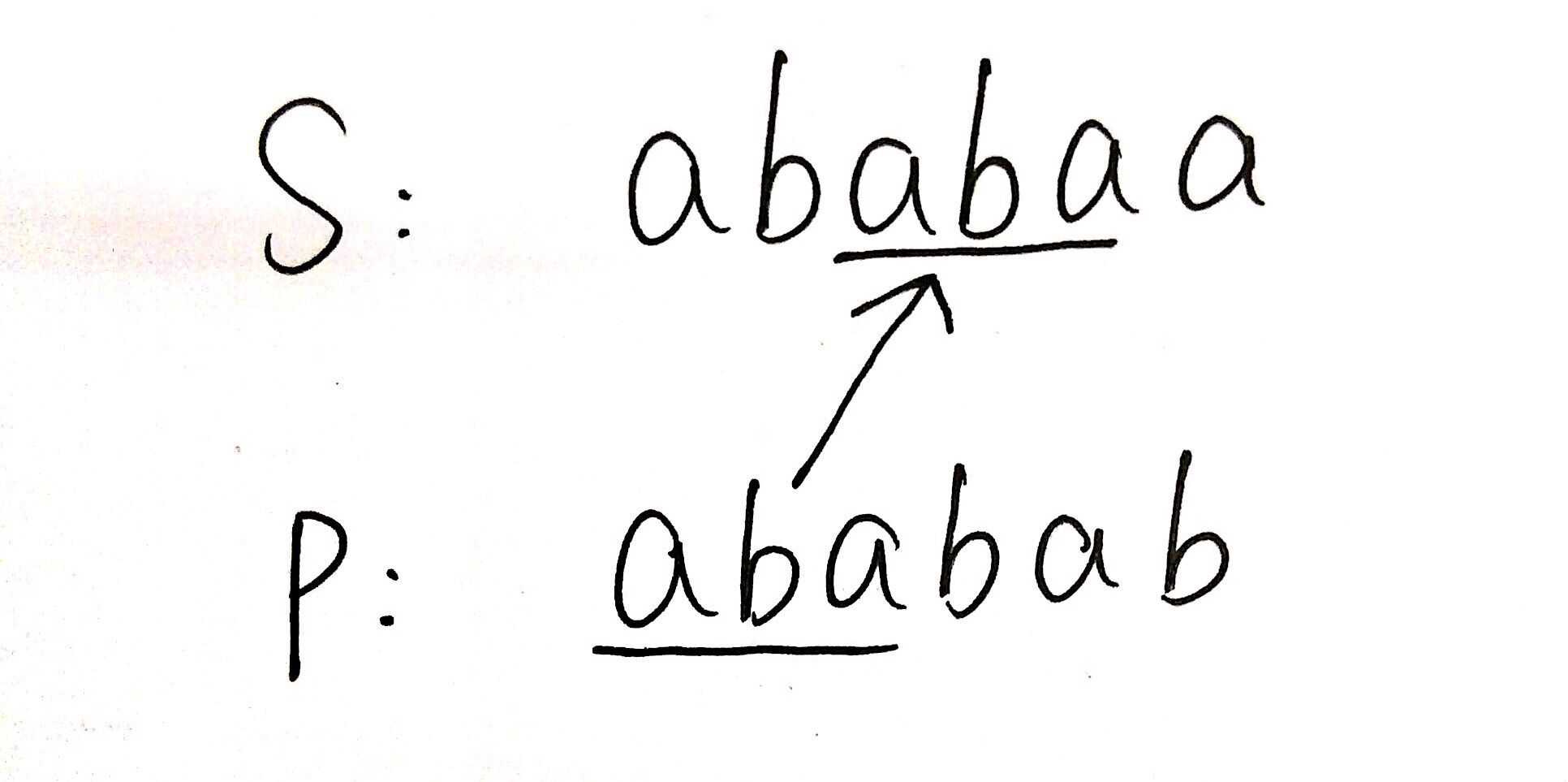
以上图所示的匹配为栗子,目前已经匹配了“ababa”(后边的先不看),再往后匹配就失败了,此时我要移动P串,KMP就不是移动一个了,而是移动k个,那么怎么决定k的大小呢,很显然,已经匹配的串的后缀和前缀是有一定重复的,这样利用重复的信息,在向后移动的时候,我们才能把前面一部分直接拿来用。
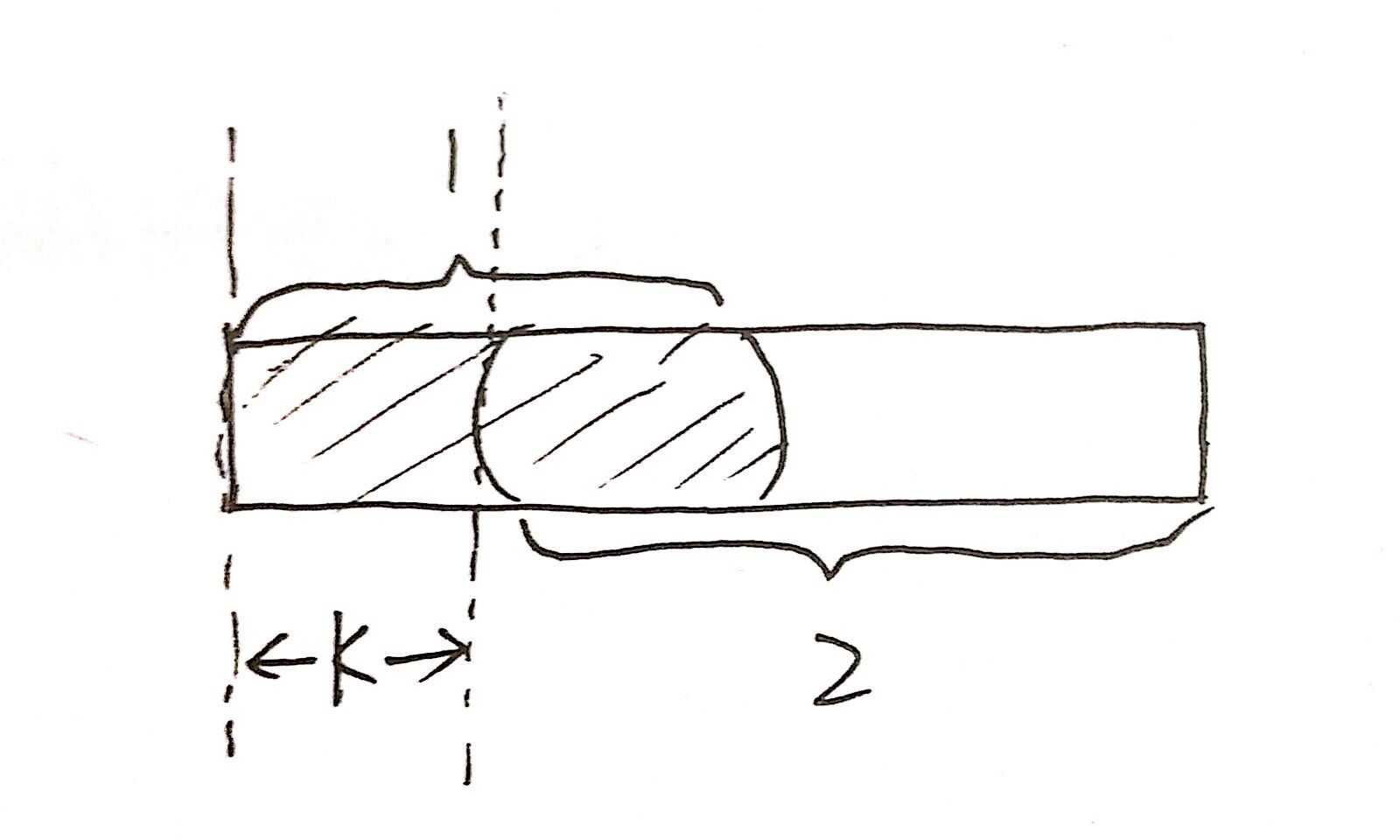
就像手绘的这张图一样,整个矩形我们目前已经匹配上了,1部分和2部分是重复的,那么我们就可以向后移动k个,即1和2重合,毫无疑问,移动后,1部分是已经匹配好的,无需再检测匹配了。
所以,我们需要找,前缀和后缀最长的公共部分的长度。很显然,公共部分越长,k就越小,说明当前越接近匹配串。为了后边便于操作,我们在预处理中,遍历得到模式串P的所有子串的最大公共部分长度,构成部分匹配表(next表),在后边匹配的时候,直接查表就可以得到下一次前进的k值。
例如在上述讲前缀后缀时的栗子,前缀和后缀最长公共部分是“aba”,因此,表中对应的值就是3。
当然,前进的k=已经匹配的字符串长度-该串对应的匹配表的值;(k>1时才有意义)
行了,我理解的KMP算法已经讲完了,最后举个栗子验证一下

用别人的一张图吧,应该没事吧~~~
这是上边所说的部分匹配表,具体怎么得到的上边已经讲了。模式串P是“abababca”,待查找的串S为“bacbababaabcbab”。
 如图,画线部分,移动之后依然对其,就不用再比较了。
如图,画线部分,移动之后依然对其,就不用再比较了。
剩下的工作类似,知道找到匹配串或者匹配失败。
标签:
原文地址:http://www.cnblogs.com/wktwj/p/4880888.html