标签:
作者 白宁超
2015年10月15日18:30:07
摘要:程序员眼中的统计学系列是作者和团队共同学习笔记的整理。首先提到统计学,很多人认为是经济学或者数学的专利,与计算机并没有交集。诚然在传统学科中,其在以上学科发挥作用很大。然而随着科学技术的发展和机器智能的普及,统计学在机器智能中的作用越来越重要。本系列统计学的学习基于《深入浅出统计学》一书(偏向代码实现,需要读者有一定基础,可以参见后面PPT学习)。正如(吴军)先生在《数学之美》一书中阐述的,基于统计和数学模型对机器智能发挥重大的作用。诸如:语音识别、词性分析、机器翻译等世界级的难题也是从统计中找到开启成功之门钥匙的。尤其是在自然语言处理方面更显得重要,因此,对统计和数学建模的学习是尤为重要的。最后感谢团队所有人的参与。( 本文原创,转载注明出处:排列组合:排序、排位、排 )
【程序员眼中的统计学(1)】 信息图形化:第一印象
【程序员眼中的统计学(2)】集中趋势度量:分散性、变异性、强大的距
【程序员眼中的统计学(3)】概率计算:把握机会
【程序员眼中的统计学(4)】离散概率分布的运用:善用期望
【程序员眼中的统计学(5)】排列组合:排序、排位、排
【程序员眼中的统计学(6)】几何分布、二项分布及泊松分布:坚持离散
【程序员眼中的统计学(7)】正态分布的运用:正态之美
【程序员眼中的统计学(8)】统计抽样的运用:抽取样本
【程序员眼中的统计学(9)】总体和样本的估计:进行预测
【程序员眼中的统计学(10)】假设检验的运用:研究证据
【程序员眼中的统计学(11)】卡方分布的应用
【程序员眼中的统计学(12)】相关与回归:我的线条如何?

定义:若具有性质A的事件有m个,具有性质B的事件有n个,则具有性质A或性质B的事件有m+n个。
例子:事件A:a点到b点乘火车有3条线路。
事件B:a点到b点乘汽车有2条线路。
则a点到b点共有(2+3)=5条不同线路
解释说明:完成一件事,有n类方法。在第1类办法中有m1种不同的方法,在第2类方法中有m2种不同的方法,……,在第n类方法中有mn 种不同的方法,则完成这件事的不同方法共有:N=m1+m2+...+mn
注意点:各类方法相互独立的。
定义:若具有性质A的事件有m个,具有性质B的事件有n个,则具有性质A与性质B的事件有m*n个。
例子:事件A:a点到b点有3条不同的路径。
事件B:b点到c点有2条不同的路径。
则a点到b点共有3*2=6条不同的路径。
解释说明:完成一件事,需要分成n个步骤。做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步与mn种不同的方法,则完成这件事的不同方法共有:N=m1*m2*mn
注意点:各个步骤相互依存。
排列的定义
设 A={a1,a2,...,an}是n个不同元素的集合,m满足0≤m≤n。任取A中m个元素按顺序排成一列,称为从A中取m个的一个无重排列。
例子:

排列符号定义
从n个不同元素中,任取m个元素的所有排列的个数叫做从n个元素的排列数,用符号![]() 表示。
表示。
排列计算公式
选排列:当m<n时的排列称为选排列。选排列数公式:
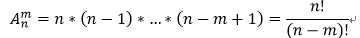
全排列:当m=n时的排列称为全排列。全排列公式:
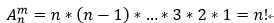
优点
可以辅助计算排列的概率问题。
缺点
此公式只适用m个元素是不同的情况,如果当m个元素有重复的时候就不能用此方法,使用受到条件限制。
排列应用
可以计算彩票的中奖概率,分析彩票的购买的排列情况,如七位数等。
圆周排列定义
从n个不同的数中不重复的取出m个沿一圆圈排列,称为一个圆周排列,表示为![]() 。
。
圆周排列符号定义
从n个不同的数中不重复的取出m个沿一圆圈排列,得到的排列数,符号表示为 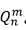 。
。
例子
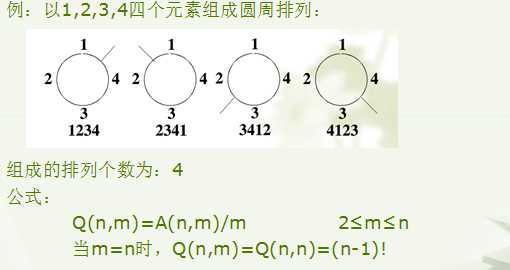
圆周排列计算公式
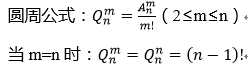
优点
可以快速计算圆周排列的排列数。
缺点
不区分圆周排列是逆时针还是顺时针排列。
圆周排列应用
在圆形的马场比赛跑道,可以计算赛马的中奖概率。
组合的定义
从n个不同元素中不重复的选取m个元素,组成一组(不管其顺序),称为从n个不同元素中选取m个元素的无重组合。
组合符号定义
从n个不同元素中不重复的选取m个元素,组成一组(不管其顺序),得到的排列数用符号 表示。
例子:

组合计算公式
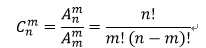
组合数的两个性质: 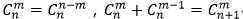 ,
,
优点
生活中经常计算概率的时候经常需要用到组合辅助计算。
缺点
输入的n个元素必须互不相同。
组合应用
可以计算彩票的中奖概率,分析彩票的购买的组合情况,如组合3。
递归法、字典序法、递增进位数制法、递减近位数制法、邻位交换法、n进制法……
递归算法
输入:{1,2,3}。输出:123,132,213,231,312,321
算法思想:第一位取1,对2,3全排列。第一位取2,对1,3全排列。第一位取3,对1,2全排列。
字典序法
算法思想:设p是集合{1、2、3、4……n}的一个全排列:p=p1p2.....pn
1、从排列的右端往左,找出第一个比右边数字小的数字序号j,也就是第一个顺序两位数。
2、从右端开始到j.找出第一个比pj大的数字pk。
3、交换pj,pk
4、对交换后的集合中p(j+1)......pn顺序逆转,也就是顺序排列。
排列算法输入数据、输出结果
* @param object 输入可选元素 * @param m 选取m个数排列 * @param out 输出排列后的元素集 * @return 输出排列总数
类和方法描述
类名:Permutation.java 方法: getCountByLine(Object[] object, long m)获取无重排列数目 getCountByCircle(Object[] object, int m)获取无重圆周排列数目 getAllPermutation(Object[] in, List<Object[]> out, int index)得到所有排列
java代码实现
/** * 获取无重线排列总数目 * 描述:从n个元数中选取m个元数进行全排列,得出一共有多少种排法 * 公式:A(m,n)=m!/(n-m)! * 优缺点:输入数据必须互不相同。求阶乘时,使用了for循环,避免了递归方法导致内存溢出的风险。 * (object数组中元素总数为n,从object数组中选出的m个数排列) * @param object 输入可选元素 * @param m 选取m个数排列 * @return 输出排列总数 */ public static BigInteger getCountByLine(Object[] object, long m) { long n = object.length; BigInteger result = MathUtils.factorial(n-m+1, n);//计算n-m+1到n的阶乘 return result; } /** * 获取无重圆周排列数目 * 描述:从n个数中选取m个数进行圆周排列,获取一共有多少种排法 * 公式:Q(m,n)=A(m,n)/m=m!/(m*(n-m)!) * 优缺点:输入数据必须互不相同。m定义了int类型,限制了计算范围。 * (object数组中元素总数为n,从object数组中选出的m个数圆周排列) * @param object 输入可选元素 * @param m 选取m个数排列 * @return 输出排列总数 */ public static BigInteger getCountByCircle(Object[] object, int m) { int n = object.length; BigInteger result = MathUtils.factorial(n-m+1, n).divide(BigInteger.valueOf(m));//计算n-m+1到n的阶乘除以m return result; } /** * 全排列(递归) * 例:输入{1,2,3}输出{1,2,3}{1,3,2}{2,1,3}{2,3,1}{3,1,2}{3,2,1} * 描述:输入一个数组,对数组中的所有元素进行全排列,把每种排列放入out集合中。 * 优缺点:输入数据必须互不相同。使用了递归的算法,当输入数据比较大时,会存在内存溢出的危险。 * @param in 输入数据 * @param out 输出数据 * @param index 默认为0 */ public static void getAllPermutation(Object[] in, List<Object[]> out, int index) { if(index == in.length-1) { Object[] outTemp = in.clone(); out.add(outTemp); } for(int i=index; i<in.length; i++) { swap(in,index,i); getAllPermutation(in,out,index+1);//递归 swap(in,index,i); } } /** * 获取所有排列 * 例:输入{1,2,3}输出{1}{2}{3}{1,2}{2,1}{1,3}{3,1}{2,3}{3,2}{1,2,3}…… * 描述:输入一个数组,先从数组中选取一个数全排列,再选取两个两个数全排列,再选取三个数全排列,把所有的得到的排列放入out集合中。 * 优缺点:输入元素必须互不相同。 * @param in 输入数据 * @param out 输出数据 */ public static void getSelectPermutaion(Object[] in, List<Object[]> out) { List<Object[]> outTemp = new ArrayList<Object[]>(); for(int i=0; i<in.length; i++) { Combination.getCombination(in, outTemp, i+1);//获取所有组合 } for(int i=0; i<outTemp.size(); i++) { getAllPermutation(outTemp.get(i), out, 0);//对每种组合进行全排列 } } /** * 交换下标为i,j两个元素 * 描述:对object数组的i,j位置的元素进行交换 * @param object * @param i * @param j */ public static void swap(Object[] object, int i, int j) { Object temp = object[i]; object[i] = object[j]; object[j] = temp; }
排列算法异常和误差
输入数据时检查数据类型,输出的数据被转换成Object类型了。
适用或不适用场景
输入的元素是互不相同的,并且有序排列。可以据此分析彩票的中奖率,比如七位数。
二进制法
算法思想:首先初始化,将数组前n个元素置1,表示第一个组合为前n个数。然后从左到右扫描数组元素值的“10”组合,找到第一个“10”组合后将其变为 “01”组合,同时将其左边的所有“1”全部移动到数组的最左端。当第一个“1”移动到数组的m-n的位置,即n个“1”全部移动到最右端时,就得到了最后一个组合。
组合算法输入数据、输出结果
* @param in 输入可选元素 * @param m 选取m个数排列 * @param out 输出组合后的元素集 * @return 返回组合后的数目
类和方法描述
类名:Combination.java 方法: getCount(Object[] in, long m)获取组合数 getCombination(Object[] in, List<Object[]> out, int m)获取组合后的所有情况
java代码实现
/** * 获取无重组合数目 * 描述:从n个数中选取m个元素组成一组,得到一共有多少种不同的组合 * 公式:C(m,n)=n!/(m!*(n-m)!) * @param in 输入可选元素 * @param m 每次选m个 * @return 返回组合后的总数目 */ public static BigInteger getCount(Object[] in, long m) { long n = in.length; BigInteger result = BigInteger.valueOf(1); if(m<2/n) {//增加计算效率 result = MathUtils.factorial(n-m+1, n).divide(MathUtils.factorial(1, m));//计算公式 } else { result = MathUtils.factorial(m+1, n).divide(MathUtils.factorial(1, n-m));//计算公式 } return result; } /** * 组合(二进制法) * 例:输入{1,2,3}从中选2个的数组合。输出:{1,2}{1,3}{2,3} * 描述:从输入的元素中,选m个元素组合,把所有的组合存在out中 * @param in 输入数组 * @param out 输出组合后的数组集 * @param m 取出m个数 */ public static void getCombination(Object[] in, List<Object[]> out, int m) { int n = in.length; int[] array = new int[n]; for(int i=0; i<n; i++) {//初始化 if(i<m) array[i] = 1; else array[i] = 0; } List<int[]> list = new ArrayList<int[]>(); boolean flag = true; while(flag) { int[] intTemp = array.clone(); list.add(intTemp); for(int i=0; i<n-1; i++) { if(array[i]==1 && array[i+1]==0) { array[i]=0;//交换i,i+1的值 array[i+1]=1; if(array[0]==0) {//把i位置左边的1都移到最左边 for(int k=0,j=0;k<i;k++) { if(array[k]==1) { array[j]=1; array[k]=0; j++; } } } break; } if(i==n-2) flag = false; } } for(int i=0; i<list.size(); i++) {//把二进制中的1转换成对应的数组 Object[] objTemp = new Object[m]; for(int j=0,k=0;j<n;j++) { if(list.get(i)[j]==1) { objTemp[k] = in[j]; k++; } } out.add(objTemp); } }
组合算法异常和误差
输入数据时检查数据类型,输入数据的可选范围是受限的。输出的数据为Object类型了,可以通过类型转换变为与输入数据一致的类型。
适用或不适用场景
输入的元素必须是互不相同的,并且属于抽取不放回的情况,抽出是无序的。可以据此分析彩票的中奖率,比如组合3。
标签:
原文地址:http://www.cnblogs.com/baiboy/p/tjx5.html