标签:
算法步骤:
①求一次最短边,将连接最短边的两个顶点标识为已经访问。
②再求一次最短边(将第一次求得的最短边排除),判断两个顶点是否构成回路,如果构成回路则不取该边,并将该边标示为已经访问;若不构成回路则选取该边为最小生成树的边。在选取一条边时,为了便于检测是否构成回路,用一个数组Vset[n]来保存每一个顶点所在的连通分量的编号。开始时令vset[i] = i,即图中每个顶点自成一个连通分量,连通分量的编号使用该顶点哎图中的位置。
③重复步骤2,直到选取了n-1条边。若未能选取n-1条边则说明该图不连通。
C语言代码:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #define MAXCOST 100 4 5 typedef struct wedge 6 { 7 int vex1;//起点 8 int vex2;//终点 9 int weight;//权重 10 int flag;//是否被访问 11 }W; 12 13 void Kruskal() 14 { 15 int i,j,k,v1,v2,*vset; 16 int n,m,costcount=0; 17 W *edgeList; 18 printf("请输入节点数:"); 19 scanf("%d",&n); 20 printf("请输入边的数量:"); 21 scanf("%d",&m); 22 vset = (int *)malloc((n+1)*sizeof(int)); 23 edgeList = (W *)malloc((m+1)*sizeof(W)); 24 for(i=1;i<=m;i++) 25 { 26 printf("第%d条边:起点,终点,权重:",i); 27 scanf("%d,%d,%d",&edgeList[i].vex1,&edgeList[i].vex2,&edgeList[i].weight); 28 edgeList[i].flag = 0; 29 } 30 31 //初始化连通分量数组 32 33 for(i=1;i<=n;i++) 34 { 35 vset[i] = i;//初始化时将每个节点设为一个连通分量 36 } 37 38 k = 0;//记录可以加的边 39 int min; 40 while(k != n-1) 41 { 42 j = 0; 43 min = MAXCOST; 44 //如果edgeList[i] 45 for(i=1;i<=m;i++) 46 { 47 if(edgeList[i].flag !=1 && min > edgeList[i].weight) 48 { 49 min = edgeList[i].weight; 50 j = i; 51 } 52 } 53 //将取出的最小边设置为已访问 54 edgeList[j].flag = 1; 55 v1 = edgeList[j].vex1;//该边的节点1 56 v2 = edgeList[j].vex2;//该边的节点2 57 //printf("(%d,%d),%d\n",v1,v2,edgeList[j].weight); 58 if(vset[v1] != vset[v2]) 59 { 60 costcount += edgeList[j].weight; 61 printf("(%d,%d),%d\n",v1,v2,edgeList[j].weight); 62 k++; 63 for(i=1;i<=n;i++) 64 { 65 if(vset[i] == vset[v2]) 66 { 67 vset[i] = vset[v1]; 68 } 69 } 70 } 71 } 72 printf("总共耗费:%d",costcount); 73 } 74 75 void main() 76 { 77 Kruskal(); 78 printf("\n"); 79 }
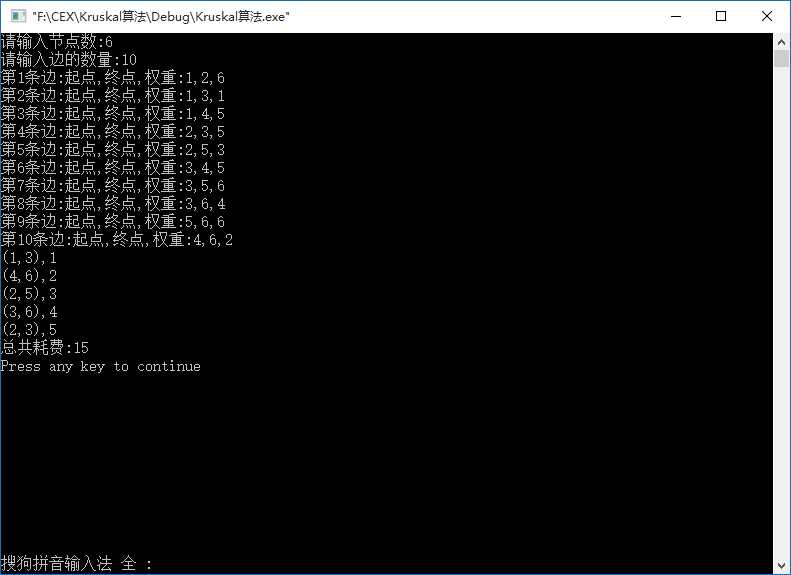
测试用例:
标签:
原文地址:http://www.cnblogs.com/shanligang/p/4883440.html