标签:
1冒泡排序:

void Bubble(int *A,int n)//冒泡算法的简单实现 { for(int i=0;i<n-1;i++) { for(int j=0;j<n-i-1;j++) { if(A[j]>A[j+1]) { int temp=A[j]; A[j]=A[j+1]; A[j+1]=temp; } } } }
改进后的冒泡排序1,增加标示位
void Bubble_1(int *A,int n)//改进后的冒泡算法,增加标示位 { bool pos=false; for(int i=0;i<n-1;i++) { pos=true; for(int j=0;j<n-i-1;j++) { if(A[j]>A[j+1]) { int temp=A[j]; A[j]=A[j+1]; A[j+1]=temp; pos=false; } } if(pos) return; } }

void Select(int *A,int n)//简单选择排序 { int min; for(int j=0;j<n-1;j++) { min=j; for(int i=j+1;i<n;i++) { if(A[min]>A[i]) min=i; } int temp=A[min]; A[min]=A[j]; A[j]=temp; } }
改进的双向选择排序
void Select_1(int *A,int n)//双向选择排序 { int min,max; for(int j=0;j<(n-1)/2;j++) { min=j; max=n-j-1; for(int i=j+1;i<n-j;i++) { if(A[min]>A[i]) min=i; if(A[max]<A[i]) max=i; } int temp=A[min]; A[min]=A[j]; A[j]=temp; temp=A[max]; A[max]=A[n-j-1]; A[n-j-1]=temp; } }

void Insert(int *A,int n)//直接插入算法 { int temp,count; if(n<2)return; for(int i=1;i<n;i++) { temp=A[i]; count=i-1; while(count>=0&&A[count]>temp) { A[count+1]=A[count]; count--; } A[count+1]=temp; } }

void ShellSort(int *A,int n)//带有步长选择的插入排序 { for(int div=n/2;div>=1;div/=2) { for(int i=div;i<n;i++) { for(int j=i;j-div>=0&&A[j]<A[j-div]&&j>=0;j-=div) /*主要看这里,与其说是插入排序,不如说是有步长选择的冒泡排序, 并不是说它不对,只是不好直观理解。*/ { int temp=A[j]; A[j]=A[j-div]; A[j-div]=temp; } } } }
void ShellSort_1(int *A,int n)//利用插入排序的模型,直观的写法。 { for(int div=n/2;div>=1;div/=2) { for(int i=div;i<n;i++) { int temp,count; temp=A[i]; count=i-div; while(count>=0&&A[count]>temp) { A[count+div]=A[count]; count-=div; } A[count+div]=temp; } } }
可以将可变步长单独写成一个函数
void ShellInsert(int *A,int n,int div) { for(int i=div;i<n;i++) { int temp,count; temp=A[i]; count=i-div; while(count>=0&&A[count]>temp) { A[count+div]=A[count]; count-=div; } A[count+div]=temp; } }
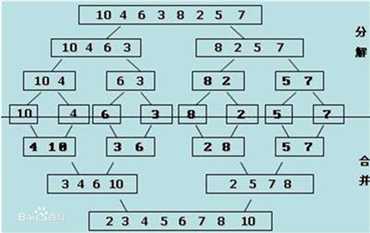
归并排序在《算法导论》里是最先接触的,也是最为基础的用来理解递归的一种算法,具有O(nlogn)的时间复杂度和O(n)的空间复杂度。
http://blog.csdn.net/hguisu/article/details/7776068
标签:
原文地址:http://www.cnblogs.com/fastcam/p/4883545.html