标签:
归并排序的基本思想是:
将<两个或两个>以上的<有序>子序列归并为<一个>有序序列
在内部排序中,通常采用的是2-路归并排序。也就是将两个位置相邻的有序子序列归并为一个有序序列。
有序子序列R[1...m]和有序子序列R[m+1...n]--->有序序列R[1...n]
① 分解 -- 将当前区间一分为二,即求分裂点 mid = (low + high)/2;
② 求解 -- 递归地对两个子区间a[low...mid] 和 a[mid+1...high]进行归并排序。<<<递归的终结条件是子区间长度为1>>>。
③ 合并 -- 将<<<已排序>>>的两个子区间a[low...mid]和 a[mid+1...high]归并为一个有序的区间a[low...high]。
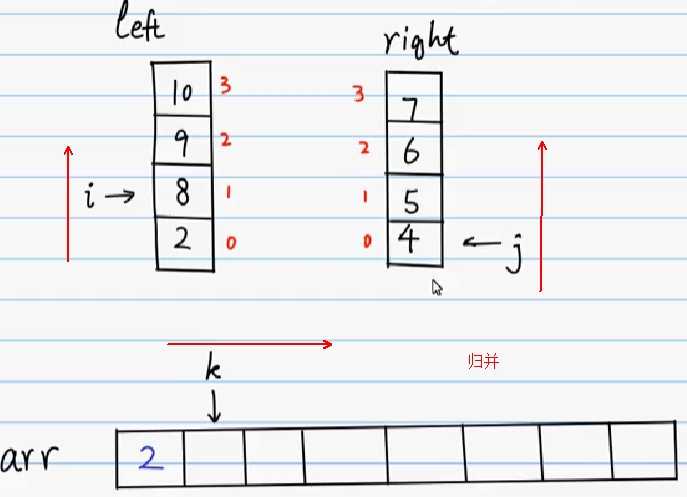
1 public class MergeSort1 { 2 // a是待排序数组,start是起始下标,end是最后一个下标 3 public static void mergeSort(int[] a, int start, int end) { 4 5 if (a == null || start >= end) 6 return; 7 8 // mid将原来的数组分成两个数组 9 int mid = start + (end - start) / 2; 10 // 递归排序a[start...<mid>] 11 mergeSort(a, start, mid); 12 // 递归排序a[<mid+1>...end] 13 mergeSort(a, mid + 1, end); 14 // a[start...<mid>]和a[<mid+1>...end]是两个有序数组了 15 // 下面将他们合并成一个 16 merge(a, start, mid, end); 17 } 18 19 // 结合图理解 20 // 将一个数组相邻两个有序区间合并成一个 21 // a包含两个有序区间的数组 22 // start:第一个有序区间的起始地址 23 // mid:第一个有序区间的结束地址 24 // end:第二个有序区间的结束地址 25 public static void merge(int[] a, int start, int mid, int end) { 26 // 汇总两个有序区间的临时区域 27 int[] temp = new int[end - start + 1]; 28 // 第一个有序区的索引 29 int i = start; 30 // 第二个有序区的索引 31 int j = mid + 1; 32 // 临时区的索引 33 int k = 0; 34 // 比较两个有序序列,将较小的数先移到新数组中。 35 // <<<这个while循环结束之后,至少有一个数组的元素<全部>放在临时数组中>>> 36 while (i <= mid && j <= end) { 37 if (a[i] < a[j]) 38 temp[k++] = a[i++]; 39 else 40 temp[k++] = a[j++]; 41 } 42 // 左边剩余的数放在临时数组中(并不知道有没有,没有拉倒) 43 while (i <= mid) 44 temp[k++] = a[i++]; 45 46 // 右边剩余的数放在临时数组中(并不知道有没有,没有拉倒) 47 while (j <= end) 48 temp[k++] = a[j++]; 49 50 // 临时数组中的元素是有序的,拷贝到数组A中 51 for (i = 0; i < temp.length; i++) 52 a[start + i] = temp[i]; 53 temp = null; 54 } 55 }
归并排序的时间复杂度和稳定性
归并排序时间复杂度
归并排序的时间复杂度是O(n*log2n) ,它的最差时间复杂度,平均时间复杂度,最好时间复杂度都是O(N*log2N)。但是它需要额外的存储空间。假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N),需要遍历多少次呢?归并排序的形式就是一棵二叉树,它需要遍历的次数就是二叉树的深度,而根据完全二叉树可以得出它的时间复杂度是O(N*log2N)。
//汇总两个有序区间的临时区域
int[] temp = new int[end - start + 1];
在实现归并排序时,需要和待排记录等数量的辅助空间,所以空间复杂度是O(N)
归并排序稳定性
归并排序是<稳定的>算法,它满足稳定算法的定义。
数列中两个相等的数在排序前后的相对位置不变,就是稳定的。
算法稳定性 -- 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
标签:
原文地址:http://www.cnblogs.com/winner-0715/p/4892110.html