标签:
AVL树是带有平衡条件的二叉查找树,这个平衡条件必须容易保持。前面我写过二叉搜索树,然而这个树的最大深度为n,最小深度为logn,因此查找时效率不是特别高,我们可以构建这样一棵树,它的最大深度始终为logn,这就是AVL树,它要求每个节点的左子树和右子树的高度最多差1的二叉查找树。(空树高度定义为-1)
AVL树的平衡必须在每一步操作中都可以保持,在插入以后,只有那些从插入点到根节点的路径上的节点的平衡条件可能会被改变,因为只有这些节点的子树可能发生变化。当我们沿着这条路径上行到根并更新平衡信息时,我们可以找到一个节点,它的新平衡破坏了AVL条件。我们将指出如何在第一个这样的节点重新平衡这棵树,并且满足AVL特性。
AVL树的平衡被破坏通常是下面的四种情况,把必须平衡的节点叫做alpha,由于节点最多有两个儿子,因此高度不平衡时,alpha的两颗子树的高度差2:
对alpha的左儿子的左子树进行一次插入;
对alpha的左儿子的右子树进行一次插入;
对alpha的右儿子的左子树进行一次插入;
对alpha的右儿子的右子树进行一次插入;
显然,第一种情况和第四种情况较为简单,只需进行一次单旋转即可:
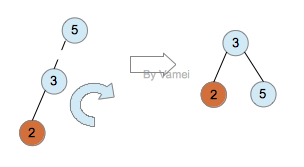
上图表明,左侧开始超重,导致5的左子树的高度明显比右子树的高度大2,因此这个时候需要进行单旋转,即将3变成根节点,将5变成3的右子树,这样就使得树继续平衡了。对于右侧超重的情况,也可类似分析。
但是,对于第二种和第三种情况,重新平衡就相对复杂一点,如下图所示:

如上图所示,节点5的左子树明显超重,但是4是3的右子树,这样就不能通过简单的单旋转来实现平衡。这里我们需要进行两次单旋转即可,首先对3进行单次右旋转,这样4就成了5的左节点,而3就变成了4的左节点,最后5/3/4的排布就变成了第一种情况,那么就可以对节点5进行单次左旋转即可。最后,4成了1的右节点,3成了4的左节点,5成了4的右节点。如下图所示:

上面就是双旋转。
其他情况可以依次类比。
/*
This is the head file for AVL data structure
*/
#ifndef _AVL_H
#define _AVL_H
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct TreeNode *PtrToNode;
typedef PtrToNode Tree;
typedef PtrToNode Position;
struct TreeNode {
int Element;
Tree Left; //节点左孩子
Tree Right; //节点右孩子
int Height;
};
int Max(int a,int b);
Position SingleRotateWithLeft(Position K2);
Position SingleRotateWithRight(Position K2);
Position DoubleRotateWithLeft(Position K3);
Position DoubleRotateWithRight(Position K3);
Tree Insert(int X, Tree T);
Position FindMax(Tree T);
Position FindMin(Tree T);
Position Find(int X, Tree T);
Tree MakeEmpty(Tree T);
void PrintWithPreorder(Tree T);
void PrintWithInorder(Tree T);
void PrintWithPostorder(Tree T);
int Height(Position P);
#include "AVL.c"
#endif
#include "AVL.h"
/*
* 使二叉树变为空,采用递归释放内存的方法
*/
Tree MakeEmpty(Tree T)
{
if (T != NULL) {
MakeEmpty(T->Left);
MakeEmpty(T->Right);
T->Height=-1;
free(T);
}
return NULL;
}
/*
* 查找某一元素
*/
Position Find(int X, Tree T)
{
if (T == NULL) {
return NULL;
}
if (X < T->Element) {
return Find(X, T->Left);
}
else if (X>T->Element) {
return Find(X, T->Right);
}
else {
return T;
}
}
/*
* 寻找最小值
*/
Position FindMin(Tree T)
{
if (T == NULL) {
return NULL;
}
else if (T->Left == NULL) {
return T;
}
else {
FindMin(T->Left);
}
}
/*
* 寻找最大值
*/
Position FindMax(Tree T)
{
if (T == NULL) {
return NULL;
}
else if (T->Right == NULL) {
return T;
}
else {
FindMax(T->Right);
}
}
/*
* 插入元素到二叉树中
*/
Tree Insert(int X, Tree T)
{
if (T == NULL) {
T = (Tree)malloc(sizeof(struct TreeNode));
if (T == NULL) {
printf("Out of memory!\n");
exit(1);
}
else {
T->Element = X;
T->Left = T->Right = NULL;
T->Height=0;
}
}
else if (X < T->Element) {
T->Left = Insert(X, T->Left);
if(Height(T->Left)-Height(T->Right)==2) {
if(X<T->Left->Element)
T=SingleRotateWithLeft(T);
else
T=DoubleRotateWithLeft(T);
}
}
else if (X > T->Element) {
T->Right = Insert(X, T->Right);
if(Height(T->Right)-Height(T->Left)==2) {
if(X>T->Right->Element)
T=SingleRotateWithRight(T);
else
T=DoubleRotateWithRight(T);
}
}
T->Height=Max(Height(T->Left),Height(T->Right))+1;
return T;
}
Position SingleRotateWithLeft(Position K2)
{
Position K1;
K1=K2->Left;
K2->Left=K1->Right;
K1->Right=K2;
K2->Height=Max(Height(K2->Left),Height(K2->Right))+1;
K1->Height=Max(Height(K1->Left),K2->Height)+1;
return K1;
}
Position SingleRotateWithRight(Position K2)
{
Position K1;
K1=K2->Right;
K2->Right=K1->Left;
K1->Left=K2;
K2->Height=Max(Height(K2->Left),Height(K2->Right))+1;
K1->Height=Max(Height(K1->Right),K2->Height)+1;
return K1;
}
Position DoubleRotateWithLeft(Position K3)
{
K3->Left=SingleRotateWithRight(K3->Left);
return SingleRotateWithLeft(K3);
}
Position DoubleRotateWithRight(Position K3)
{
K3->Right=SingleRotateWithLeft(K3->Right);
return SingleRotateWithRight(K3);
}
int Max(int a,int b)
{
return (a>b)?a:b;
}
/*
* 前序遍历打印所有元素
*/
void PrintWithPreorder(Tree T)
{
if (T != NULL) {
printf("%d\t", T->Element);
PrintWithPreorder(T->Left);
PrintWithPreorder(T->Right);
}
}
/*
* 中序遍历打印所有元素
*/
void PrintWithInorder(Tree T)
{
if (T != NULL) {
PrintWithInorder(T->Left);
printf("%d\t", T->Element);
PrintWithInorder(T->Right);
}
}
/*
* 后序遍历打印所有元素
*/
void PrintWithPostorder(Tree T)
{
if (T != NULL) {
PrintWithPostorder(T->Left);
PrintWithPostorder(T->Right);
printf("%d\t", T->Element);
}
}
/*
* 返回节点的高度
*/
int Height(Position P)
{
if(P == NULL)
return -1;
else
return P->Height;
}
#include "AVL.h"
int main()
{
Tree T = NULL;
T = Insert(3, T);
T = Insert(2, T);
T = Insert(1, T);
T = Insert(4, T);
T = Insert(5, T);
T = Insert(6, T);
T = Insert(7, T);
T = Insert(16, T);
T = Insert(15, T);
T = Insert(14, T);
printf("Min is %d\n", FindMin(T)->Element);
printf("Max is %d\n", FindMax(T)->Element);
//下面采用中序遍历方式打印所有节点元素
PrintWithPreorder(T);
printf("\n");
return 0;
}
标签:
原文地址:http://my.oschina.net/zzw922cn/blog/519252