morris算法-----高级二叉树遍历算法

标签：

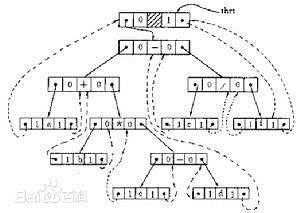
　　在遍历儿叉树时，常常使用的是递归遍历，或者是借助于栈来迭代，在遍历过程中，每个节点仅访问一次，所以这样遍历的时间复杂度为O(n)，空间复杂度为O(n)，并且递归的算法易于理解和实现。在遍历过程中，递归遍历过程的空间复杂度却是O(n)，就算是转换为使用栈空间迭代时间，还是没有改变算法对额外空间的需求，在学习数据结构课程时，还学习了线索二叉树，在线索二叉树中，使用线索来保存节点的前驱和后继的信息，而这些线索是利用了叶节点的空指针域来保存，所以知道了树种每个节点的前驱和后继的位置（指针）可以有效降低遍历过程中对空间的需求，但是使用线索二叉树必须先通过一次二叉树遍历算法，为二叉树建立线索，此外还需要标记每个节点的指针域是线索还是指针，使每个结点都有了唯一前驱和后继（第一个结点无前驱，最后一个结点无后继）。对于二叉树的一个结点，查找其左右子女是方便的，其前驱后继只有在遍历中得到。为了容易找到前驱和后继，有两种方法。一是在结点结构中增加向前和向后的指针fwd和bkd，这种方法增加了存储开销，不可取；二是利用二叉树的空链指针。现将二叉树的结点结构重新定义如下：

下面来看看Morris二叉树遍历算法。 

　　Morris算法与递归和使用栈空间遍历的思想不同，它使用二叉树中的叶节点的right指针来保存后面将要访问的节点的信息，当这个right指针使用完成之后，再将它置为NULL，但是在访问过程中有些节点会访问两次，所以与递归的空间换时间的思路不同，Morris则是使用时间换空间的思想，这里讲的很简单，大体意思每次去找当前节点的左子树的最右子节点，最右子节点的右节点指向当前根节点，然后以左子树为根节点，再找其左子树的最右子节点，最右子节点再指向当前的根节点。这是我自己的理解，以中序遍历为例。下面是代码实现：

public static void morrisIn(Node head){
    if (head==null){
        return;
    } 
      Node cur1=head;
      Node cur2=null;
      while(cur1 !=null){
         cur2=cur1.left;
         if(cur2!=null){
            while (cur2.right !=null && cur2.right!=cur1){
            cur2=cur2.right;
           }
           if(cur2.right ==null ){
           cur2.right =cur1;
           cur1 = cur1.left;
            continue;
          }else {
                cur2,right=null;  
          }
      }
      Sysetem.out.print(cur1.value+" "); 
      cur1=cur1.right;     
    }
     System.out.println();  
}    

前序遍历就是第一次访问的该节点是就答应该节点，代码示例略。

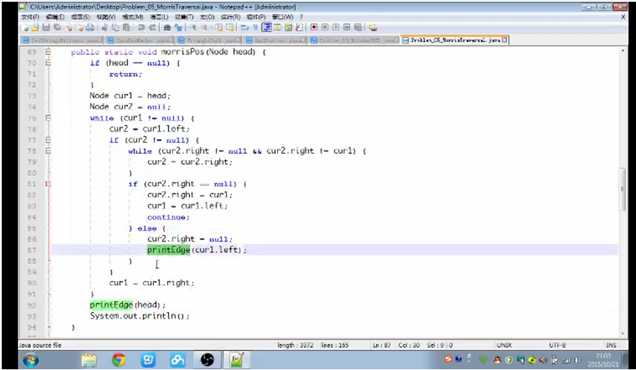
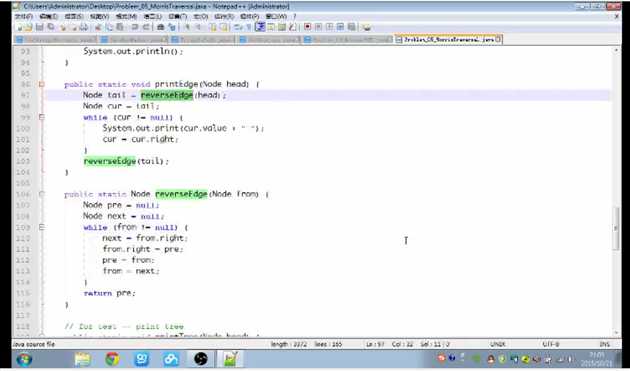
后序遍历比较复杂，即在访问该节点的左子树的最右子节点时，最右子节点的子节点之前为空，由于现在指向着该节点，即打印时机为第二次访问到一个根节点是，倒序打印该根节点的左子树的整个最右子树。程序差不都，掌握打印时机即可。（再加一个倒序打印左子树的整个最右子树函数即可），代码贴图如下：

morris算法-----高级二叉树遍历算法

标签：

原文地址：http://www.cnblogs.com/floridezzh/p/4899347.html