标签:
希尔排序
希尔排序是计算机科学家Donald L.Shell 而得名,他在1959年发现了希尔排序算法。希尔排序基于插入排序,但是增加了一个新的特性,大大提高了插入排序的执行效率。
插入排序:复制的次数太多
由于希尔排序是基于插入排序的,所以需要回顾下“插入排除”。在插入排除执行的一半的时候,标记符左边这部分数据项都是排过序的(这些数据之间是有序的),而记右边的数据项没有排过序。这个算法取出标记符所指的数据项,把它存储在一个临时的变量。接着,从刚刚被移除的数据项的左边第一个单元看是,每次把有序的数据项向右移动一个单元,直到存储在临时变量里的数据项能够有序回插。
下面是插入排序带来的问题。假设一个很小的数据项在很靠近右端的位置上,这里本来应该是值比较大的数据项所在的位置。把这个小数据项移动到在左边的正确位置上,所有的中间数据项(这个数据项原来所在的位置和它应该移动到的位置之间的数据项)都必须向右移动一位。这个步骤对每一个数据项都执行了将近N次的复制。虽不是所有数据项都必须移动N个位置但是数据项平均移动了N/2个位置,这就执行了N次N/2个移位,总共是N2/2次复制。因此,插入排序的执行效率是O(N2)。
如果能以某种方式不必一个一个地移动所有中间的数据项,就能把较小的数据项移动到左边,那么这个算法的执行效率就会有很大的改进。
n-增量排序
希尔排序通过加大插入排序中元素之间的间隔,并在这些有间隔的元素中进行插入排序,从而是数据项能大跨度地移动。当这些数据项排过一趟序后,希尔排序算法减小数据项的间隔在进行排序,依次进行下去。进行这些排序时数据项之间的间隔被称为增量,并且习惯上用字母h来表示。图7.1显示了增量为4时对包含10个数据项的数组进行排序的第一个步骤的情况。在0、4和8号位置上的数据项已经有序了。

图 7.1 4-增量排序0、4、和8号数据项
当对0、4和8号数据项完成排序之后,算法向右移一步,对1、5和9号数据项进行排序。这个排序过程持续进行,直到所有的数据项都已经完成了4-增量排序,也就是说所有间隔为4的数据项之间都已经排列有序。这个过程如图7.2所示(使用更为简洁形象的图例表示)。
在完成以4位增量的希尔排序之后,数组可以看成是由4个子数组组成:(0、4、8),(1、5、9),(2、6)和(3、7),这四个子数组内分别是完全有序的。这些子数组相互交错着排列,然而彼此独立。

图7.2 完整的以4为增量的一趟排序
注意,在这个例子中,在完成以4为增量的希尔排序后,素有元素离它在最终有序序列中的位置相差都不到两个单元。这就是数组“基本有序”的含义,也正是希尔排序的奥秘所在。通过创建这种交错的内部有序的数据项集合,把完成排序所必需的工作量降到了最小。
插入排序对基本有序的数组排序是非常有效的。如果插入排序只需要把数据项移动一位或者两位,那么算法大概需要O(N)时间。这样,当数组完成4-增量排序之后,可以进行普通的插入排序,即1-增量排序。4-增量排序和1-增量排序结合起来应用,比前面不执行4-增量排序而仅仅应用普通的插入排序要快得多。
减小间隔
上面已经演示了以4为初始间隔对包含10个数据项的数组进行排序的情况。对于更大的数组,开始的间隔也应该更大。然后间隔不断减小,直到间隔变成1。
举例来说,含有1000个数据项的数组可能先以364为增量,然后以121为增量,以40为增量,以13为增量,以4为增量,最后以1为增量进行希尔排序。用来形成间隔的数列(在本例中为364,121,40,13,4,1)被称为间隔序列。这里所表示的间隔序列由Knuth提出,此序列是很常用的。数列以逆向的形式从1开始,通过递归表示
h = 3*h+1
来产生,初始值为1。表7.1的前两栏显示了这个公式产生的序列。
表7.1 Knuth间隔序列
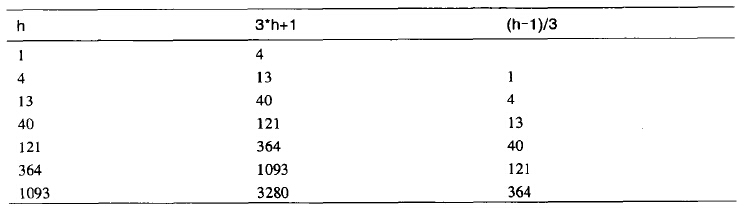
还有一些其他的方法也能产生间隔序列;后面会讲到这个问题。首先,来研究使用Knuth序列进行希尔排序的情况。
在排序算法中,首先在一个短小的循环中使用序列的生成公式计算出最初的间隔。h值最初被赋为1,然后应用公式h=3*h+1生成序列,1、4、13、40、121、364,等等。当间隔大于数组大小的时候这个过程停止。对于一个含有1000个数据项的数组,序列的第七个数字,1093就太大了。因此,使用序列的第六个数字作为最大的数字来开始这个排序过程,作364-增量排序。然后,每完成一次排序例程的外部循环,用前面提供的此公式的倒推式来减小间隔:
h = (h-3)/3
它在表7.1的第三栏中显示。这个倒推的公式生成逆置的序列 364、121、40、13、4、1从364开始,以每一个数字作为增量进行排序。当数组用1-增量排序后,算法结束。
希尔排序的Java代码
package com.goaji.shellsort;
public class ArraySh{
private long[] theArray;
private int nElems;
public ArraySh(int max){
theArray = new long[max];
nElems = 0;
}
public void insert(long value){
theArray[nElems] = value;
nElems++;
}
public void display(){
System.out.print("A=");
for (int i = 0; i < nElems; i++) {
System.out.print(theArray[i] + " ");
}
System.out.println("");
}
public void shellSort(){
int inner,outer;
long temp;
int h=1;
while(h<=nElems/3)
h = h*3+1;
while(h>0){
for (outer = 0; outer < nElems; outer++) {
temp = theArray[outer];
inner = outer;
while(inner>h-1 && theArray[inner-h]>=temp){
theArray[inner] = theArray[inner-h];
inner-=h;
}
theArray[inner] = temp;
}
h = (h-1)/3;
}
}
}
public static void main(String[] args) {
int maxSize = 10;
ArraySh arr;
arr = new ArraySh(maxSize);
for (int i = 0; i < maxSize; i++) {
long n = (int)(java.lang.Math.random()*99);
arr.insert(n);
}
arr.display();
arr.shellSort();
arr.display();
}
//输出:
A=26 87 14 50 14 9 53 37 50 83
A=9 14 14 26 37 50 50 53 83 87
可以是maxSize取更大的值,但是也不要太大。对10000个数据项需要将近1分钟的时间来完成排序;
尽管希尔排序的算法只需要几行代码来实现,但是跟踪这个算法也不是很简单的。
其他间隔序列
选择间隔序列可以称得上是一种魔法。这里只讨论了公式h=h*3+1生成间隔序列,但是应用其他间隔序列也取得了不同程度的成功。只有一个绝对的条件,就是逐渐减小的间隔最后一定要等于一,因此最后一趟排序是一次普通的插入排序。
希尔排序的效率
迄今为止,除了在一些特殊的情况下,还没有人能够从理论上分析希尔排序的效率。有各种各样基于试验的评估,估计它的时间级从O(N3/2)到O(N的7/6次方)。
标签:
原文地址:http://my.oschina.net/u/1431757/blog/521911