标签:
依然延续第一篇读书笔记,这一篇是基于《ACM/ICPC 算法训练教程》上关于线段树的讲解的总结和修改(这本书在线段树这里Error非常多),但是总体来说这本书关于具体算法的讲解和案例都是不错的。
线段树简介 这是一种二叉搜索树,类似于区间树,是一种描述线段的树形数据结构,也是ACMer必学的一种数据结构,主要用于查询对一段数据的处理和存储查询,对时间度的优化也是较为明显的,优化后的时间复杂为O(logN)。此外,线段树还可以拓展为点树,ZWK线段树等等,与此类似的还有树状数组等等。
例如:要将数组s[]从[i,j]段上的元素均加上b,那么我们通常需要遍历每个元素(s[i],s[i+1]...s[j])并+b,此时使用的操作数为(j-i+1)次,但如果我们在某些情况下只关心[i,j]段内的总和呢,此时我们只需在[i,j]段内总和sum的基础上+b*(j-i+1)就行了,这样的操作数只需要一次。
再者,若想知道[i,j]段内的和,直接输出此前存储的总和sum,这样比每次查询时都要遍历(j-i+1)个元素要好得多,因此参照树形结构可以引入一种表示一条线段上数据的结构。
用数组模拟树可以直观表述线段树如右图: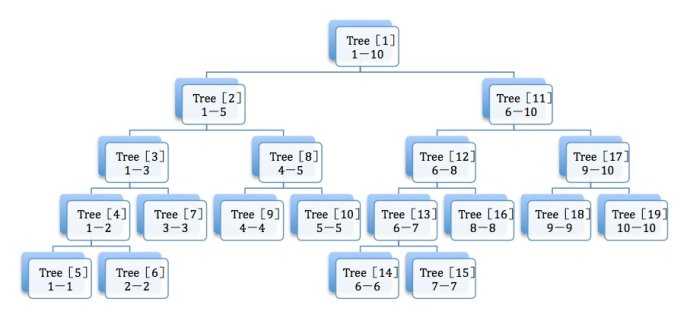
具体实现和相应改进Code:
定义
每个结点的定义可以暂时如下:
struct Node{ int l, r; int value; }tree[MAXN];
上面是一种简单直接的表示,但是对于需要经常更新数值的线段树来说,这种定义让线段树的时间优化变得优势全无。
因为如果对每一个[i,j]内的线段上每一个元素+b时,作为一段数据,我们可以+b*(j-i+1),但这一段的子树上的数据又该如何表示呢,难道一直遍历下去直到所有子结点遍历完并更新其中的数据嘛,这明显是个很愚蠢的做法,这样做会使得线段树的效率下降不少。
我们在结点的定义上引入一个增量add(初始为0),使得每次更新数据时,在该结点及其子树全部更新数据后,再在该结点的增量add上+b,这样在每次查询或更新到它的子结点时,必然会遍历到该结点,此时查询该结点的add是否为0,如果不为0,则将add的值向下传递,更新子树结点上的value。(在需要时才进行更新是一个很好的算法优化)
因此我们可以改进上面关于结点的定义,最终定义如下:
1 /*Tree*/ 2 struct Node{ 3 int l, r; 4 int value; 5 int add; 6 }tree[MAXN];
搭建
那么我们该如何搭建一个线段树呢,我们利用树形结构的思想,不断得二分得到左儿子和右儿子。原结点的value就靠左右儿子的value相加得到。
具体如下:
1 /*从x结点开始扩展线段树*/ 2 void build(int x, int l, int r) 3 { 4 tree[x].l = l; 5 tree[x].r = r; 6 if (l == r){ 7 tree[x].value = source[l]; 8 return; 9 } 10 int mid = (l + r) / 2; 11 build(x * 2, l, mid); 12 build(x * 2 + 1, mid + 1, r); 13 tree[x].value = tree[2 * x].value + tree[2 * x + 1].value; 14 tree[x].add = 0; 15 }
更新
此处开始对书上的Code做了修改和改进。
那么为了进行一段数据上数据的更新,我们在上面已经引入了add增量表示,具体做法如下:
1 /*更新-在[l,r]线段上加上m*/ 2 void update(int x, int l, int r, int m) 3 { 4 // update 5 tree[x].value += m*(r - l + 1); 6 // Hit! 7 if (tree[x].l == l && tree[x].r == r){ 8 tree[x].add += m; 9 return; 10 } 11 // add - Transfer 12 if (tree[x].add){ 13 tree[2 * x].add += tree[x].add; 14 tree[2 * x].value += tree[x].add*(tree[2 * x].r - tree[2 * x].l + 1); 15 tree[2 * x + 1].add += tree[x].add; 16 tree[2 * x + 1].value += tree[x].add*(tree[2 * x + 1].r - tree[2 * x + 1].l + 1); 17 tree[x].add = 0; 18 } 19 // continue - Search 20 int mid = (tree[x].l + tree[x].r)/2; 21 if (r <= mid) //[l,r]在mid右侧 22 update(2 * x, l, r, m); 23 else if (l >= mid) //[l,r]在mid左侧 24 update(2 * x + 1, l, r, m); 25 else{ //[l,r]横跨mid 26 update(2 * x, l, mid, m); 27 update(2 * x + 1, mid + 1, r, m); 28 } 29 }
查询
也就是查询某段上的数据value
1 //最终查询值 2 int ans = 0; 3 /*查询*/ 4 void query(int x, int l, int r) 5 { 6 // Hit! 7 if (tree[x].l == l && tree[x].r == r) 8 { 9 ans += tree[x].value; 10 return; 11 } 12 // add - Transfer 13 if (tree[x].add){ 14 tree[2 * x].add += tree[x].add; 15 tree[2 * x].value += tree[x].add*(tree[2 * x].r - tree[2 * x].l + 1); 16 tree[2 * x + 1].add += tree[x].add; 17 tree[2 * x + 1].value += tree[x].add*(tree[2 * x + 1].r - tree[2 * x + 1].l + 1); 18 tree[x].add = 0; 19 } 20 // continue - Search 21 int mid = (tree[x].l + tree[x].r)/2; 22 if (r <= mid) //[l,r]在mid左侧 23 query(2 * x, l, r); 24 else if (l >= mid) //[l,r]在mid右侧 25 query(2 * x + 1, l, r); 26 else{ //[l,r]横跨mid 27 query(2 * x, l, mid); 28 query(2 * x + 1, mid + 1, r); 29 } 30 }
另外对于一个源数组source[MAX],线段树往往所需的空间要稍大一点,大约为4*MAX.
《ACM/ICPC 算法训练教程》读书笔记 之 数据结构(线段树详解)
标签:
原文地址:http://www.cnblogs.com/Inkblots/p/4919193.html