标签:
Hi All,
After I investigated ccr below, I found an rounding issue. The issue is that we can get different result
between Linux and Windows platform when we do the decimal rounding with string format or print
function.
Please refer to the screenshots first.
Pic1 Windows program and result.
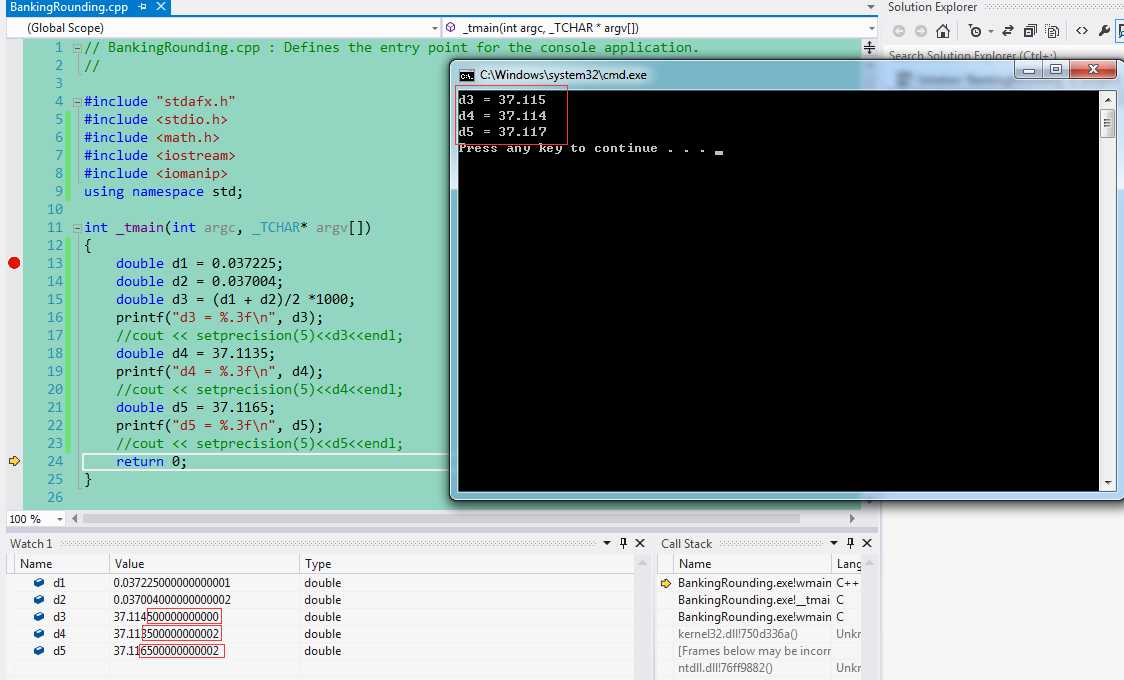
Pic1 Windows program and result.
Pic2 & Pic3 Linux program and result
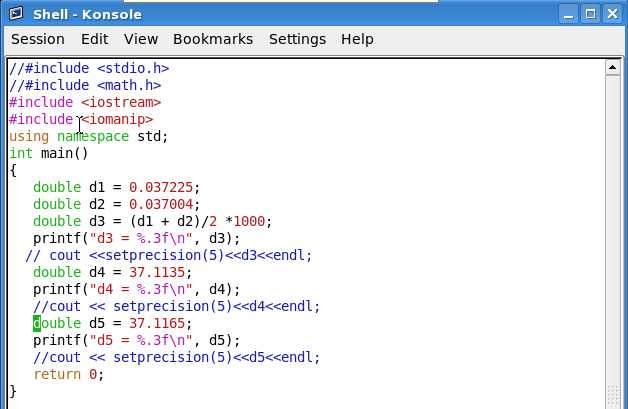
Pic2 Linux Program
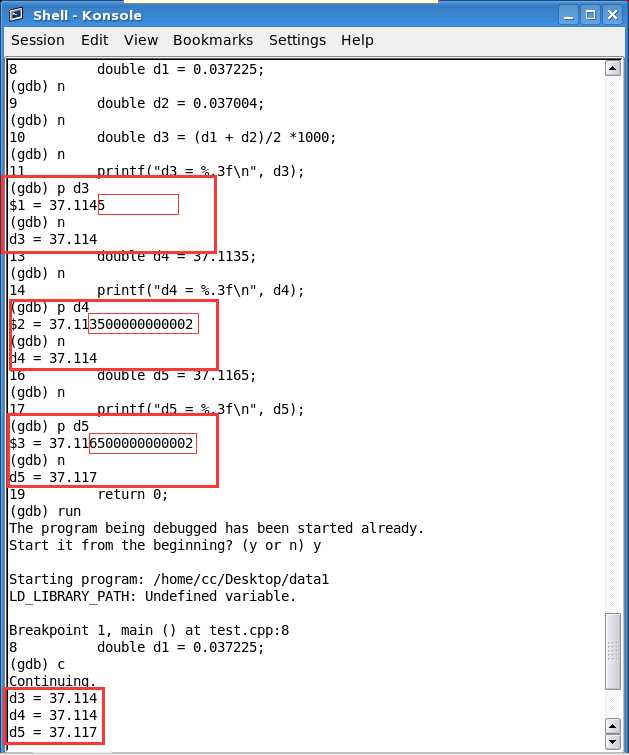
Pic3 Linux Result
I use the same simple program on Linux and Windows to describe this situation.
On Windows, from Pic1, the variables are
d3 = 37.114500000000000 d3 = 37.115
d4 = 37.113500000000002 result d4 = 37.114
d5 = 37.116500000000002 d5 = 37.117
On Linux , from Pic2, the variables are
d3 = 37.114500000000000 d3 = 37.114
d4 = 37.113500000000002 result d4 = 37.114
d5 = 37.116500000000002 d5 = 37.117
The apparent difference is the value of d3 in result. This is also the behavior of this CCR.
After searching Google, I find the reason is the different algorithm used in Linux and Windows when doing the decimal rounding.
On Windows, decimal rounding uses the common rounding off. However, On Linux, it uses the banking rounding.
Decimal rounding takes different algorithm principle between GNU C library in Linux and CRT library in Windows.
Please refer to the explanation as below.
Common method (Windows C/C++ used)
This method is commonly used in mathematical applications, for example in accounting. It is the one generally taught in elementary mathematics classes. This method is also known as Asymmetric Arithmetic Rounding or Round-Half-Up (Asymmetric Implementation)
1. Divide it by the unit to which it is to be rounded
2. Round it to the nearest whole number, unless it ends in exactly .5
3. If it ends in exactly .5, then add 0.5
4. Multiply it by the unit to which it is to be rounded
Examples (rounded to hundredths):
As the name implies, this can introduce a bias: if all the unrounded numbers had four decimal places, say, then in our example the expected average of the rounded numbers will be 0.0005 higher than that of the unrounded numbers.
This method, also known as unbiased rounding, convergent rounding, statistician‘s rounding, Dutch rounding, Gaussian rounding, or bankers‘ rounding, exactly replicates the common method of rounding except when the digit(s) following the rounding digit starts with a five and has no non-zero digits after it.
Despite the custom of rounding the number 4.5 up to 5, in fact 4.5 is no nearer to 5 than it is to 4 (it is 0.5 away from both). When dealing with large sets of scientific or statistical data, where trends are important, traditional rounding on average biases the data upwards slightly. Over a large set of data, or when many subsequent rounding operations are performed as in digital signal processing, the round-to-even rule tends to reduce the total rounding error, with (on average) an equal portion of numbers rounding up as rounding down. This generally reduces upwards skewing of the result.
The new algorithm becomes (only rule 3. changes):
1. Divide it by the unit to which it is to be rounded
2. Round it to the nearest whole number, unless it ends in exactly .5
3. If it ends in exactly .5, then round towards the nearest even whole number
4. Multiply it by the unit to which it is to be rounded
Examples (rounded to hundredths):
More details, please refer to
<1> http://www.cnblogs.com/samcn/archive/2009/06/05/1497094.html
<2> https://zh.wikipedia.org/wiki/%E6%95%B0%E5%80%BC%E4%BF%AE%E7%BA%A6
<3> https://en.wikipedia.org/wiki/Rounding#Round_half_to_even
There is switch for linux to decide which kind of rounding used when programming.
Banking Rounding for Decimal rounding off on Linux
标签:
原文地址:http://www.cnblogs.com/gycui/p/4940221.html