标签:
题目
给定一个由 n 个整数组成的数组和一个正整数 s ,请找出该数组中满足其和 ≥ s 的最小长度子数组。如果无解,则返回 -1。
给定数组 [2,3,1,2,4,3] 和 s = 7, 子数组 [4,3] 是该条件下的最小长度子数组。
如果你已经完成了O(n)时间复杂度的编程,请再试试 O(n log n)时间复杂度。
解题
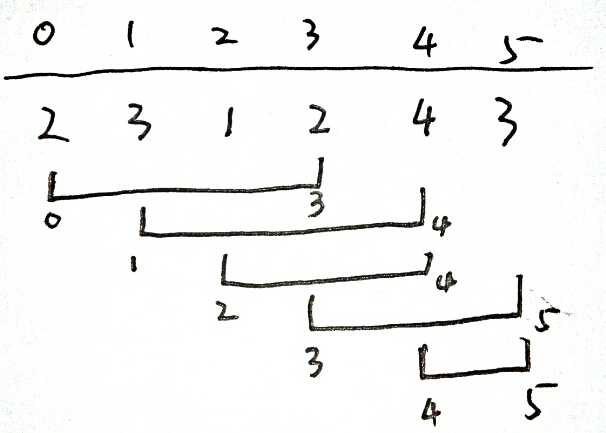
定义两个指针,slow,fast,以先后速度向右走
fast先找到第一个是的sum>s的值
根据fast和slow计算当前子数组的长度
sum-=nums[slow],寻找最后一个不满足sum>=s 的slow,每次更新子数组长度的最短值。
这里一般会问什么没有对数组排序的问题,这里的数组都是正数,如果是负数会出现问题,这里怎么加,sum值都是增加的,顺序至少影响增加的速度的问题,同时我们向前走到了sum>=s的值后还要对后面的slow的部分进行检查。这样解释的不是很充分,具体我也不知道了。
还要网上说时间复杂度是O(N),我怎么感觉时间复杂度应该很接近O(N2),不知道为什么?
操作如下图所示

public class Solution { /** * @param nums: an array of integers * @param s: an integer * @return: an integer representing the minimum size of subarray */ public int minimumSize(int[] nums, int s) { // write your code here if(nums.length == 0 || nums == null) return -1; int slow = 0; int fast = 0; int res = Integer.MAX_VALUE; int sum = 0; while(fast < nums.length){ while( fast < nums.length && sum < s){ sum += nums[fast]; fast += 1; // System.out.println(sum+" "+fast); } // System.out.println(); while(sum>=s){ res = Math.min(res,fast - slow); sum -=nums[slow]; slow +=1; } } return res==Integer.MAX_VALUE?-1:res; } }
总耗时: 1910 ms

class Solution: # @param nums: a list of integers # @param s: an integer # @return: an integer representing the minimum size of subarray def minimumSize(self, nums, s): # write your code here if s == None or len(nums) == 0: return -1; lens = len(nums) slow = 0 fast = 0 sum = 0 res = lens+1 while fast < lens: while fast < lens and sum < s: sum += nums[fast] fast +=1 while slow < fast and sum>= s: res = min(res,fast - slow) sum -= nums[slow] slow +=1 if res ==lens+1: return -1 else: return res
总耗时: 444 ms
lintcode 中等题:Minimum Size Subarray 和大于S的最小子数组
标签:
原文地址:http://www.cnblogs.com/theskulls/p/4957460.html