POJ3009 Curling 2.0(DFS 好题)

On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.

Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)

The movement of the stone obeys the following rules:

• At the beginning, the stone stands still at the start square.
• The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
• When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. 2(a)).
• Once thrown, the stone keeps moving to the same direction until one of the following occurs:
  • The stone hits a block (Fig. 2(b), (c)).
    • The stone stops at the square next to the block it hit.
    • The block disappears.
  • The stone gets out of the board.
    • The game ends in failure.
  • The stone reaches the goal square.
    • The stone stops there and the game ends in success.
• You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.

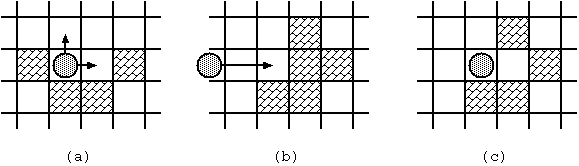
Fig. 2: Stone movements

Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.

With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).

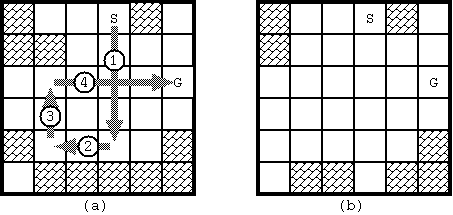
Fig. 3: The solution for Fig. D-1 and the final board configuration

The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.

Each dataset is formatted as follows.

the width(=w) and the height(=h) of the board 
First row of the board 
... 
h-th row of the board

The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.

Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.

0	vacant square
1	block
2	start position
3	goal position

The dataset for Fig. D-1 is as follows:

6 6 
1 0 0 2 1 0 
1 1 0 0 0 0 
0 0 0 0 0 3 
0 0 0 0 0 0 
1 0 0 0 0 1 
0 1 1 1 1 1

For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.

把一个冰壶从起点“2”用最少的步数移动到终点“3”

其中0为移动区域，1为石头区域，冰壶一旦想着某个方向运动就不会停止，也不会改变方向（想想冰壶在冰上滑动），除非冰壶撞到石头1 或者 到达终点 3

思路：每次静止的时候都有四个方向供选择，当这个方向是0时才能继续走，然后就沿着这个方向走，沿着这个方向走的处理方法就是一个while(1)来处理的，判断一下沿着走时可以遇到的情况

注意一个剪枝：k >= step return ;

 1 #include <iostream>
 2 #include <cstring>
 3 #include <algorithm>
 4 #include <cstdio>
 5 using namespace std;
 6 
 7 const int MAX = 30;
 8 int g[MAX][MAX];
 9 int w,h,step;
10 int gx,gy,sx,sy;
11 int go[4][2] ={{1,0},{-1,0},{0,1},{0,-1}};
12 void dfs(int x,int y,int k)
13 {
14     if(k >= step)
15         return;
16     for(int i = 0; i < 4; i++)
17     {
18         int fx = x + go[i][0];
19         int fy = y + go[i][1];
20 
21         if(fx >= 1 && fx <= w && fy >= 1 && fy <= h)
22         {
23             if(g[fx][fy] != 1)
24             {
25                 int flag = 0;
26                 while(1)
27                 {
28                     if(g[fx][fy] == 1)
29                     {
30                         flag = 1;
31                         break;
32                     }
33                     else if(g[fx][fy] == 3)
34                     {
35                         if(step > k)
36                             step = k;
37                         return;
38                     }
39                     fx = fx + go[i][0];
40                     fy = fy + go[i][1];
41                     if(fx <1 || fy < 1 || fx > w || fy > h)
42                         break;
43                 }
44                 if(flag)
45                 {
46                     g[fx][fy] = 0;
47                     dfs(fx - go[i][0],fy - go[i][1],k + 1);
48                     g[fx][fy] = 1;
49                 }
50             }
51 
52         }
53     }
54 }
55 int main()
56 {
57     while(scanf("%d%d",&h,&w) != EOF)   //w,h这里被坑了一下
58     {
59         if(w == 0 && h == 0)
60             break;
61         memset(g,0,sizeof(g));
62         for(int i = 1; i <= w; i++)
63         {
64             for(int j = 1; j <= h; j++)
65             {
66                 scanf("%d", &g[i][j]);
67                 if(g[i][j] == 2)
68                 {
69                     sx = i;
70                     sy = j;
71                 }
72             }
73         }
74         step = 11;
75         dfs(sx,sy,1);
76         if(step == 11)
77             printf("-1\n");
78         else
79             printf("%d\n",step);
80     }
81     return 0;
82 }

View Code