标签:
1.对小规模子数组使用插入排序
用不同的方法处理小规模问题能改进大多数递归算法的性能,因为递归会使小规模问题中方法的调用过于频繁,所以改进对它们的处理方法就能改进整个算法。对排序来说,我们已经知道插入排序(或者选择排序)非常简单,因此很可能在小数组上比归并排序更快。和之前一样,一幅可视轨迹图能够很好地说明归并排序的行为方式。图中的可视轨迹图显示的是改良后的归并排序的所有操作。使用插入排序处理小规模的子数组(比如长度小于15)一般可以将归并排序的运行时间缩短10%~15%。

2.测试数组是否已经有序
我们可以添加一个判断条件,如果a[mid]小于等于a[mid+1],我们就认为数组已经是有序的并跳过merge()方法。这个改动不影响排序的递归调用,但是任意有序的子数组算法的运行时间就变为线性的了。
关键代码:
private final int CUTOFF = 7;
private void sort(Comparable[] src, Comparable[] dst,
int lo, int hi) {
// if (hi <= lo) return;
if (hi <= lo + CUTOFF) {
insertionSort(dst, lo, hi);
return;
}
int mid = lo + (hi - lo) / 2;
sort(dst, src, lo, mid);
sort(dst, src, mid+1, hi);
// if (!less(src[mid+1], src[mid])) {
// for (int i = lo; i <= hi; i++) dst[i] = src[i];
// return;
// }
// using System.arraycopy() is a bit faster than the above loop
if (!less(src[mid+1], src[mid])) {
System.arraycopy(src, lo, dst, lo, hi - lo + 1);
return;
}
merge(src, dst, lo, mid, hi);
}
private void insertionSort(Comparable[] a, int lo,
int hi) {
for (int i = lo; i <= hi; i++)
for (int j = i; j > lo && less(a[j], a[j-1]); j--)
exch(a, j, j-1);
}
运行结果:
千万级
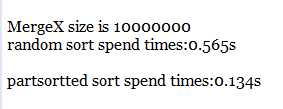
亿级
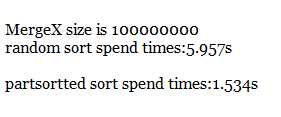
亿级,下面的random是改良前的归并9.071秒,partsortted是插入排序0.244秒
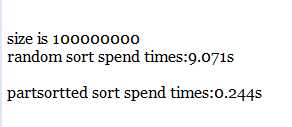
3.排序算法的复杂度
没有任何基于比较的算法能够保证使用少于lg(N!)~NlgN次比较将长度为N的数组排序。
这个结论告诉了我们在设计排序算法的时候能够达到的最佳效果。例如,如果没有这个结论,我们可能会去尝试设计一个在最坏情况下比较次数只有归并排序的一半的基于比较的算法。这个结论告诉我们这种努力是没有意义的——这样的算法不存在。这是一个重要结论,适用于任何我们能够想到的基于比较的算法。
但归并排序的最优性并不是结束,也不代表在实际应用中我们不会考虑其他的方法了,因为本文中的理论还是有许多局限性的,例如:
□归并排序的空间复杂度不是最优的;
□在实践中不一定会遇到最坏情况;
□不进行比较也能将某些数据排序。
【源码下载】
标签:
原文地址:http://www.cnblogs.com/joey-hua/p/4982821.html