标签:
冒泡排序的时间复杂度为O(n2),虽然很多排序的时间复杂度都是O(n2),但是冒泡排序的O(n2)则显得非常比较大。
简单的说,一般情况下,冒泡排序是很不好的排序,非常慢,但是作为排序算法的入门算法,它的基本思想很是重要。
冒泡排序是交换排序的一种,需要两层循环,以升序排序为例,
第一次循环把最第1大值放在序列倒数第1的位置
第一次循环把最第2大值放在序列倒数第2的位置
第一次循环把最第3大值放在序列倒数第3的位置
......
第一次循环把最第n大值放在序列倒数第n的位置
下面给出实现:
void bubble_sort(int *array,int n) { assert(array); int i,j; for(i=0;i<n;i++) for(j=1;j<n-i;j++)//要保证索引 j-1 和 j 不越界 if(array[j-1]>array[j])//大的往后移 swap(array[j-1],array[j]); }
在很多情况下,第一层循环还未循环完,序列就已经顺序了,这个时候就可以退出函数,而不是等第一层循环完在退出函数
当第二层循环不发生元素交换,那么说明序列已经顺序,用swapped记录是否发生交换
//冒泡 一改 void bubble_sort1(int *array,int n) { assert(array); int swapped=1; int i,j; for(i=0;i<n&&swapped;i++) { swapped=0; for(j=1;j<n-i;j++) if(array[j-1]>array[j])//大的往后移 { swapped=1;//发生过交换 swap(array[j-1],array[j]); } } }
前面都是把元素从头往后排序,也就是把大的元素往后放,同样的,把小的元素往前放,也能实现同样的排序。
那么往前放和往后放有什么区别呢?
对于序列 2 3 1 4
对于正排 2 3 1 4-->2 1 3 4-->1 2 3 4需要循环2次
对于逆排 2 3 1 4-->1 2 3 4需要循环1次
1 //冒泡 二改 2 void bubble_sort2(int *array,int n) 3 { 4 assert(array); 5 int i,j; 6 7 for(i=0;i<n;i++) 8 { 9 for(j=1;j<n-i;j++) 10 if(array[j-1]>array[j])//大的往后移 11 swap(array[j-1],array[j]); 12 for(j=n-i-2;j>i;j--) 13 if(array[j-1]>array[j])//小的往前移 14 swap(array[j-1],array[j]); 15 } 16 }
综合bubble_sort1和bubble_sort2,有
1 //冒泡 三改 2 void bubble_sort3(int *array,int n) 3 { 4 assert(array); 5 int i,j; 6 int swapped=1; 7 8 for(i=0;i<n&&swapped;i++) 9 { 10 swapped=0; 11 for(j=1;j<n-i;j++) 12 if(array[j-1]>array[j])//大的往后移 13 { 14 swap(array[j-1],array[j]); 15 swapped=1; 16 } 17 if(0==swapped) 18 break; 19 for(j=n-i-2;j>i;j--) 20 if(array[j-1]>array[j])//小的往前移 21 { 22 swap(array[j-1],array[j]); 23 swapped=1; 24 } 25 } 26 }
下面对这四个函数进行实际测试
#include<stdio.h> #include<stdlib.h> #include<time.h> #include<assert.h> #define swap(a,b) (a^=b,b^=a,a^=b) #define N 100000 void print(int *,int); int main() { int a[4][N]; int i; int beg,end; //定义一个存储4个函数指针的数组 void (*sort[4])(int *,int n)={bubble_sort,bubble_sort1,bubble_sort2,bubble_sort3}; char *str[4]={"bubble_sort ","bubble_sort1","bubble_sort2","bubble_sort3"}; srand((unsigned)time(NULL)); printf("正在生成数组...\n"); beg=clock(); for(i=0;i<N;i++)//生成数组的每个元素 { a[0][i]=rand()%90+10;//元素范围为[10,99] a[1][i]=rand()%90+10; a[2][i]=rand()%90+10; a[3][i]=rand()%90+10; } end=clock(); printf("生成数组完毕,用时 %lfs\n",(double)(end-beg)/CLOCKS_PER_SEC); //print(a[0],N); for(i=0;i<4;i++) { beg=clock(); sort[i](a[i],N); end=clock(); //print(a[i],N); printf("%s花费时间为 %lfs\n",str[i],(double)(end-beg)/CLOCKS_PER_SEC); } getchar(); return 0; } void print(int *array,int n) { int i; for(i=0;i<n;i++) printf("%d ",array[i]); printf("\n"); }
运行结果如下:
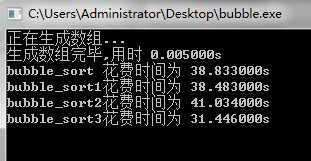
对长度为10万的基本整形数组排列后,二改的效率反而降低,这是因为要进行正向排序和逆向排序,导致内层循环从一个变到了两个,增加了循环次数。
一改和原算法效率并没有多大提升,有的时候效率反而还略微不如以前,这是因为一改的算法增加了许多次int的赋值,但是减少了很多次元素的比较,在一些比较元素很费时(比如给字符串们排序)的排序中,一改的优越性马上就会体现出来。
显然三改后的算法是四者中最好的。
标签:
原文地址:http://www.cnblogs.com/inori/p/4985678.html