标签:
准备总结几篇关于 Markov Chain Monte Carlo 的笔记。
本系列笔记主要译自 A Gentle Introduction to Markov Chain Monte Carlo (MCMC) 文章下给出的链接。
蒙特卡洛方法是用来近似计算积分的,通过数值方法也可以计算积分:最简单的近似方法是通过求小矩边梯形的面积再累加。但是当函数的维度太高,变量数太多的时候,数值方法就不适用了,蒙特卡洛方法从概率学的角度进行积分的近似计算。
我们经常需要计算下面形式的积分:
\(I = \int_{a}^b h(x)g(x)dx\)
对于某些关于随机变量 \(X\) 的函数 \(f(x)\), 其期望值可以通过下面的公式计算:
\(E[x] = \int_{p(x)}p(x)f(x)dx\)
其中 \(p(x)\) 为变量\(X\) 的密度函数,它在定义域上的积分应该为1。
事实上,如果 \(g(x)\) 满足下面的条件:
1. 在区间 \((a,b)\) 上非负
\(g(x)\geqslant0, x\in(a,b)\)
2. 在区间上的积分有限
\(\int_a^b g(x)=C<\infty\)
那么,\(g(x)\) 就可以转换为密度函数
\(p(x)=\frac{g(x)}{C}\)
只需要在积分号前乘以相应的\(C\),就可以保证原积分不变了。那么修改成密度函数后有什么好处呢?修改成密度函数的好处就是:可以通过随机模拟符合这个密度分布的变量\(x\),来求出原积分的近似值:
根据大数定理:
\(E[f(X)] = \int f(x)p(x)dx \approx \frac{1}{S}\sum_{n=1}^S f(x_s)\)
其中\(x_s\sim p(X)\), 这一点很关键,也就是说,生成的随机数必须要符合密度函数为 \(p(X)\) 的分布,只有这样,计算出来的平均值才是积分的近似值。
为了对这种方法进行理论分析,下面给出两个定理:
大数定理 对于一个已知分布的随机序列,当取样数趋于无穷时,其均值趋向于期望。
事实上,在日常生活中我们常常是这么做的,比如统计一年级某门成绩的期望,我们可以随机选一些学生进行抽测,用他们的平均成绩来近似估计该年级的成绩期望,选的学生越多,其均值就越逼近真实期望值。
在统计背景下,\(A(n)\) 是 \(B\) 的一个一致估计量(consistent estimator),如果满足在 \(n\) 趋于无穷时,\(A(n)\) 收敛于 \(B\),也就是说:对任意概率 \(P[0<P<1]\),任意值 \(\delta\),我们都可以找到 \(k\),使得对任意 \(n>k\), \(A(n)\) 与 \(B\) 的差距在 \(\delta\) 内的概率大于 \(P\)。
中心极限定理 大量独立随机变量的和近似服从标准正态分布。独立同分布(i.i.d)的随机变量 \(z_i\),均值为 \(\mu\),方差为 \(\sigma^2\):
\(\frac{\sum\limits_{i=1}^n z_i-n\mu}{\sigma\sqrt{n}}\sim\mathcal{N}(0,1)\ as\ n\rightarrow \infty\)
因此,蒙特克洛方法的误差为:
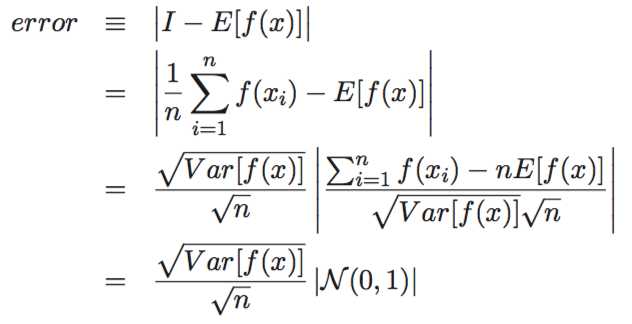
可以看出:
1. 如果 \(f(x)\) 的方差是有限的,那么 MC 估计是一致的
2. MC 估计的误差是渐进无偏的
3. MC 估计的误差近似正态分布的
4. MC 估计误差的标准差是 \(\sigma=\frac{\sqrt{Var[f(x)]}}{\sqrt{n}}\)
同时,可以发现,MC 估计对数据的维度天然免疫,无论维度多大,只需要按分布函数生成随机变量,计算随机变量的函数值,计算这些函数值的均值,即可得到对积分的估计。由于误差的标准差越小,估计越精确,因此,我们可以通过增大取样数目 \(n\) 的方式来增大 MC 估计的准确性。另一个增加准确性的思路是降低 \(f(x)\) 的方差,这类方法称为 variance-reducing techniques 这里(我)不(没)做(看)介(懂)绍。
通常的教程中介绍这个例子时会说:正方形中均匀生成的随机点落到圆内的概率为balabala,所以圆的面积比上正方形的面积为balabala,所以圆周率为balabala。这种方法固然好让人理解,但是如何严格地用公式表示这个过程呢?
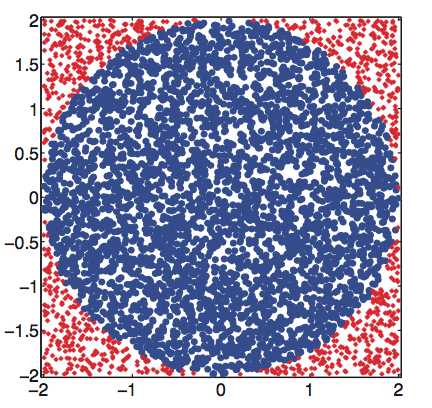
圆的面积可以用下面的积分来获得:
![]()
其中![]() 在符合内部条件\(x^2+y^2\leq r^2\)时为1,在不符合内部条件时为0。也就是说,点在圆的内部时,函数值为1,点在圆外部时函数值为0。令 \(p(x)\),\(p(y)\) 符合 \([-r,r]\) 上的均匀分布,因此,\(p(x)=p(y)=\frac{1}{2r}\)。
在符合内部条件\(x^2+y^2\leq r^2\)时为1,在不符合内部条件时为0。也就是说,点在圆的内部时,函数值为1,点在圆外部时函数值为0。令 \(p(x)\),\(p(y)\) 符合 \([-r,r]\) 上的均匀分布,因此,\(p(x)=p(y)=\frac{1}{2r}\)。
所以,根据蒙特卡洛积分,\(I = \int_{a}^b f(x)g(x)dx\) ,这里的 \(f(x)\) 转换为二维函数相当于 \(1(x^2+y^2\leq r^2)\),\(g(x)\) 相当于 1,我们把它转化为二维的密度函数,也就是\(p(x,y)=p(x)\cdot p(y)=\frac{1}{4r^2}=\frac{g(x,y)}{4r^2}\)。
所以,
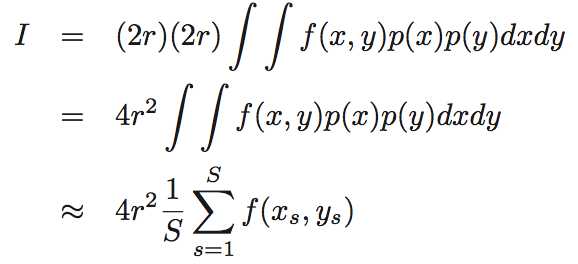
也就是,只需要生成 -r 到 r 均匀分布的横坐标和纵坐标,然后带入\(1(x^2+y^2\leq r^2)\) 判断其是否在圆内,在的话记为1,不在记为0,加和后除以点的总数,计算出落到圆内的概率,最后乘以 \(4r^2\) 求出圆的面积,知道了圆的面积,又知道半径了,自然也可以求出圆周率的近似值。
% Radious of circle r = 1; S = 10000; % Generate S points uniformly distributed points x = unifrnd(-r,r,S,1); y = unifrnd(-r,r,S,1); % The points falled into the circle fxy = (x.^2+y.^2-r^2<=0); area = 4*r^2/S*sum(fxy); pi_estimate = area/r^2; % Visualization figure; inside = fxy; outside = logical(1-fxy); scatter(x(inside),y(inside),15,‘r‘,‘filled‘); hold on; scatter(x(outside),y(outside),15, ‘b‘,‘filled‘); axis equal; xlim([-1,1]); ylim([-1,1]);
我们想计算 \(I = \int_0^1 xe^xdx\) , 由分部积分公式,不难得到其积分值为1。下面通过蒙特卡洛方法求其近似值,看是否与1接近。
可以把\(f(x)\) 看成 \(xe^x\),\(g(x)\) 看成 1,由于积分区间长度也是1,故概率分布的密度函数为\(p(x)=\frac{gx}{\int_0^1 g(x)dx}=1\)。
所以,根据上文的讨论,只需要在0到1中均匀取得随机数,然后带入\(f(x)=xe^x\) 中计算函数值,最后求均值即可得到积分的近似。
代码如下:
rng(‘default‘); % 100 sample S1 = 100; x1 = unifrnd(0,1,S1,1); y1 = x1.*exp(x1); I1 = sum(y1)/S1; % 10000 samples S2 = 10000; x2 = unifrnd(0,1,S2,1); y2 = x2.*exp(x2); I2 = sum(y2)/S2;
关于Beta分布,详细的资料请移步百度文库,这里只介绍一点:beta分布含有两个参数 A,B。对于随机变量 \(X\sim Beta(A,B)\),\(E(x)=\frac{A}{A+B}\)。
计算 Beta 分布的期望,使用如下公式:
\(E(x)=\int_{p(x)}p(x)xdx\), where \(x\sim Beta(\alpha_1\alpha_2)\)
1. 首先我们发现 \(f(x)=x\),而\(p(x)\) 本身就是概率密度函数,所以不用进行转换。
2. 我们根据概率分布 \(p(x)=Beta(\alpha_1,\alpha_2)\) 来生成大量随机的点,然后带入 \(f(x)=x\),求出其均值,即为 Beta 分布的期望。
rand(‘seed‘,12345);
alpha1 = 2; alpha2 = 10;
N = 10000;
x = betarnd(alpha1,alpha2,1,N);%生成10000个按Beta分布的点
% MONTE CARLO EXPECTATION
expectMC = mean(x);%由MC方法算出的期望近似值
% ANALYTIC EXPRESSION FOR BETA MEAN
expectAnalytic = alpha1/(alpha1 + alpha2);%Beta分布的理论期望值
% DISPLAY
figure;
bins = linspace(0,1,50);%将[0,1]区间分成50份,最后一份是大于50的部分
counts = histc(x,bins);%统计每个小区间内落入的随机点的数目
probSampled = counts/sum(counts);%Beta分布的点落入每个小区间对应的概率
probTheory = betapdf(bins,alpha1,alpha2);%每个区间点的理论概率密度值
b = bar(bins,probSampled); colormap hot; hold on;%概率分布直方图,注意这里每个竖条代表的是对应区间的概率,不是概率密度。当它除以区间长度时才是概率密度
t = plot(bins,probTheory/sum(probTheory),‘r‘,‘Linewidth‘,2)%这里probTheory/sum(probTheory)相当于是probTheory*dx,因为sum(probTheory*dx)=1, dx=1/sum(probTheory)
m = plot([expectMC,expectMC],[0 .1],‘g‘)%期望的近似值
e = plot([expectAnalytic,expectAnalytic],[0 .1],‘b‘)%期望的理论值
xlim([expectAnalytic - .05,expectAnalytic + 0.05])
legend([b,t,m,e],{‘Samples‘,‘Theory‘,‘$\hat{E}$‘,‘$E_{Theory}$‘},‘interpreter‘,‘latex‘);
title([‘E_{MC} = ‘,num2str(expectMC),‘; E_{Theory} = ‘,num2str(expectAnalytic)])
hold off
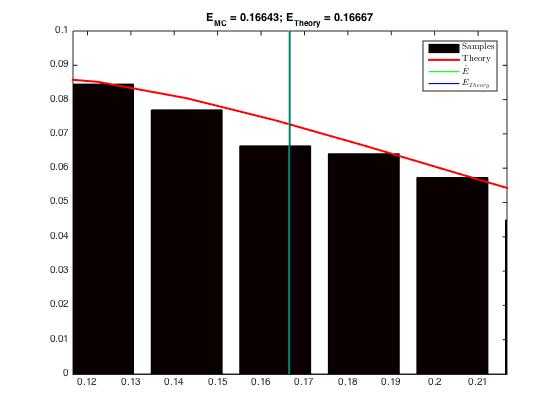
从图中我们可以看到两条竖线十分接近,也就是说由样本估计的均值十分接近真实值。
蒙特卡洛方法还可以用来求解优化问题:
\(x_{opt}=\arg\max\limits_x Cp(x)\)
如果 \(g(x)\) 满足之前提到的两条性质:1. 非负 2. 积分有限
那么,就可以将其放缩为密度函数:
\(p(x) = \frac{g(x)}{C}\)
其中 \(C = \int_x g(x) dx\)
原优化问题变形为:
\(x_{opt}=\arg\max\limits_x Cp(x)\)
以 \(p(x)\) 为概率密度函数生成随机数,那么,在随机数密度最大的地方,对应的密度函数必然也是最大的,而密度函数与目标函数之间只差一个常数的放缩,故而该位置也是目标函数最大的地方,也就是说,这一点就是优化问题的近似解。
实例
求解优化问题 \( x_{opt}=\arg\max\limits_x e^{-\frac{(x-4)^2}{2}}\)
通过求导,令导函数为零,可以求得极值点为 x=4。
同时可以观察到,被优化函数\(g(x)\)与正态分布只差了一个参数:\( \sqrt{2\pi}\)
原问题可以变形为:
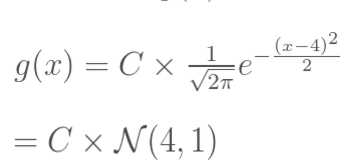
其中\(C=\sqrt{2\pi}\)。
因此,可以借助matlab生成均值为4,方差为1的正态分布随机变量,然后找出其密度函数最大的点对应的横坐标,此即为优化问题的解。
代码如下:
% MONTE CARLO OPTIMIZATION OF exp(x-4)^2
randn(‘seed‘,12345)
% INITIALZIE
N = 100000;
x = 0:.1:6;
C = sqrt(2*pi);
g = inline(‘exp(-.5*(x-4).^2)‘,‘x‘);
ph = plot(x,g(x)/C,‘r‘,‘Linewidth‘,3); hold on%画出密度函数
gh = plot(x,g(x),‘b‘,‘Linewidth‘,2); hold on;%画出待优化函数
y = normpdf(x,4,1);
% CALCULATE MONTE CARLO APPROXIMATION
x = normrnd(4,1,1,N);
bins = linspace(min(x),max(x),100);%生成100个随机区间
counts = histc(x,bins);%统计100个区间中每一个区间落入的随机点数
[~,optIdx] = max(counts);%找到落入点最多的区间的下标
xHat = bins(optIdx);%找到优化问题的近似解
% OPTIMA AND ESTIMATED OPTIMA
oh = plot([4 4],[0,1],‘k‘);
hh = plot([xHat,xHat],[0,1],‘g‘);
set(gca,‘fontsize‘,16)
legend([gh,ph,oh,hh],{‘g(x)‘,‘$p(x)=\frac{g(x)}{C}$‘,‘$x_{opt}$‘,‘$\hat{x}$‘},‘interpreter‘,‘latex‘,‘Location‘,‘Northwest‘);
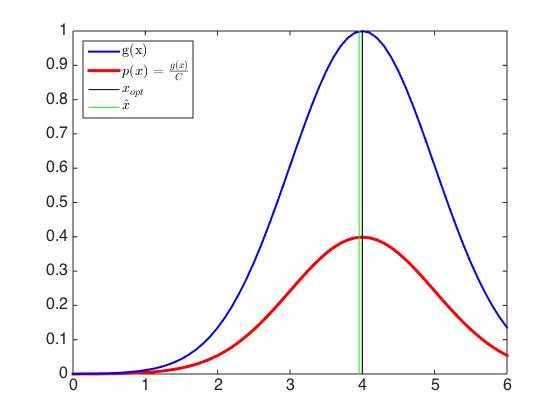
可以看到,通过蒙特卡洛算法得到的优化问题的解与真实解基本一致。
标签:
原文地址:http://www.cnblogs.com/yinxiangnan-charles/p/4999549.html