标签:
随机算法---遗传算法
遗传算法( Genetic Algorithms,GA) 是在1975 年首次由美国密西根大学的D。J。Holland 教授和他的同事们借鉴生物界达尔文的自然选择法则和孟德尔的遗传进化机制基础之上提出的。经过近30年的研究、应用,遗传算法已被广泛地应用于函数优化、机器人系统、神经网络学习过程、模式识别、图象处理、工业优化控制等领域。
遗传算法是将问题的每一个可能性解看作是群体中的一个个体(染色体),并将每一个染色体编码成串的形式,再根据预定的目标函数对每个个体进行评价,给出一个适应值。算法将根据适应度值进行它的寻优过程,遗传算法的寻优过程是通过选择、杂交和变异三个遗传算子来具体实现的。它的搜索能力由选择算子和杂交算子决定,变异算子则保证了算法能够搜索到问题空间的尽可能多的点,从而使其具有搜索全局最优的能力。要使遗传算法有效工作必须按照遗传算法的模式定理(或积木块假设) 根据具体问题设计合理的编码方案。
在运行遗传算法程序时,需要对一些参数作事先选择,它们包括种群的大小、染色体长、交叉率、变异率、最大进化代数等,这些参数对GA 的性能都有很重要的影响。在试验中参数一般选取如下:种群大小N= 20~100 ,交叉概率 = 0.4 ~0.9 ,变异概率 = 0.001~0.1 ,最大进化代数maxgen = 100~500。
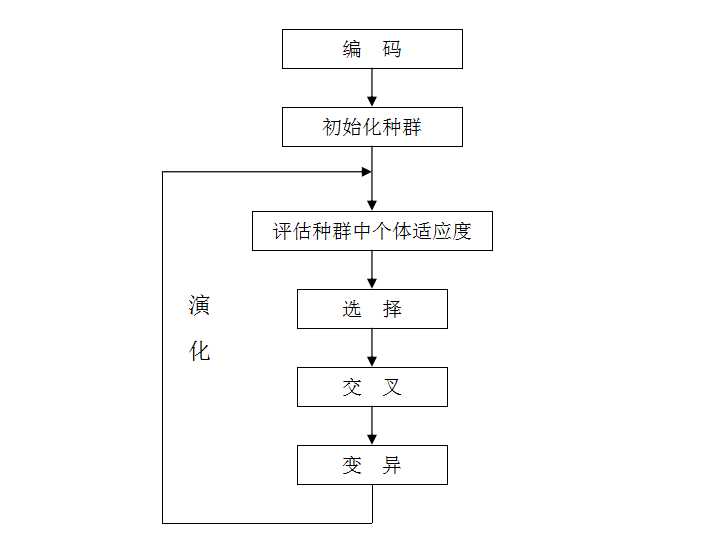
遗传算法是具有“生成+检测”的迭代过程的搜索算法。它的基本处理流程如图1所示。
图1、遗传算法的基本流程
遗传算法的基本流程描述如下:
(1)编码:将解空间的解数据进行二进制编码,表达为遗传空间的基因型串(即染色体)结构数据,如将数据9编码为“1001”;
(2)初始化种群:定义整数pop_size作为染色体的个数,并且随机产生pop_size个染色体作为初始种群;
(3)评估种群中个体适应度:评价函数对种群中的每个染色体(chromosome)求得其个体适应度;
(4)选择:选择把当前群体中适应度较高的个体按某种规则或者模型遗传到下一代种群中,这里所用的规则是:染色体在种群中被选择的可能性与其个体的适应度的大小成正比;
(5)交叉:定义参数作为交叉操作的概率,由(4)选择得到的两个个体以概率交换各自的部分染色体,得到新的两个个体;
(6)变异:定义参数作为变异操作的概率,由(5)得到每个个体中的每个基因值都以概率进行变异;
(7)演化:经过选择、交叉和变异操作,得到一个新的种群,对上述步骤经过给定的循环次数(maxgen)的种群演化,遗传算法终止。

/* 用遗传算法求y=x*sin(10*pi*x)+2的最大值 -1=<x<=2 精确到6位小数 pow(2,21)<3*1000000<pow(2,22) 编码的二进制长度为22 */ #include <stdio.h> #include <string.h> #include <stdlib.h> #include <time.h> #include <math.h> #define N 3000000 #define PI 3.14159265 #define MAX(a,b) ((a)>(b)?(a):(b)) #define SIZE 50 #define MAXGEN 50 #define P_CORSS 0.75 #define P_MUTATION 0.05 #define LEN 22 typedef struct node { char x[LEN]; double fitness,fitsum; } node; node cur[SIZE],next[SIZE],max,min; double randd() { return (double)rand()/RAND_MAX; } int randi(int k) { return (int)(randd()*k+0.5); } //计算当前种群中各个个体的适应度 void cal_fitness() { int i,j,k; double d; for(i=0; i<SIZE; i++) { k=0; for(j=LEN-1; j>=0; j--) k=(k<<1)+cur[i].x[j]; d=(double)k/N*3-1; cur[i].fitness=d*sin(10*PI*d)+2; cur[i].fitsum=i>0?(cur[i].fitness+cur[i-1].fitsum):(cur[0].fitness); } } void init() { int tmp; for(int i=0; i<SIZE; i++) { tmp=randi(N); for(int j=0; j<LEN; j++) { cur[i].x[j]=tmp%2; tmp=tmp>>1; } } cal_fitness(); } int sel() { double p=randd(); double sum=cur[SIZE-1].fitsum; for(int i=0; i<SIZE; i++) { if(cur[i].fitsum/sum>p) return i; } } //换代 void tran() { int i,j,pos; //找当前种群最优个体 max=cur[0]; for(i=1; i<SIZE-1; i++) { if(cur[i].fitness>max.fitness) max=cur[i]; } for(int k=0; k<SIZE; k+=2) { //选择交叉个体 i=sel(); j=sel(); //选择交叉位置 pos=randi(LEN-1); //交叉 if(randd()<P_CORSS) { memcpy(next[k].x,cur[i].x,pos); memcpy(next[k].x+pos,cur[j].x+pos,LEN-pos); memcpy(next[k+1].x,cur[j].x,pos); memcpy(next[k+1].x+pos,cur[i].x+pos,LEN-pos); } else { memcpy(next[k].x,cur[i].x,LEN); memcpy(next[k+1].x,cur[j].x,LEN); } //变异 if(randd()<P_MUTATION) { pos=randi(LEN-1); next[k].x[pos]^=next[k].x[pos]; pos=randi(LEN-1); next[k+1].x[pos]^=next[k+1].x[pos]; } } //找下一代的最差个体 min=next[0],j=0; for(i=1; i<SIZE-1; i++) { if(next[i].fitness<min.fitness) min=next[i],j=i; } //用上一代的最优个体替换下一代的最差个体 next[j]=max; memcpy(cur,next,sizeof(cur)); cal_fitness(); } //打印个体适应度和二进制编码 void print(node tmp) { printf("%.6lf",tmp.fitness); for(int i=0; i<LEN; i++) printf(" %d",tmp.x[i]); printf("\n"); } //打印种群 void printcur() { for(int i=0; i<SIZE; i++) print(cur[i]); } void GA() { int cnt=0; double ans; while(cnt++<MAXGEN) { tran(); // printf("%.6lf\n",max.fitness); // printcur(); } ans=cur[0].fitness; for(int i=1; i<SIZE; i++) ans=MAX(ans,cur[i].fitness); printf("%.6lf\n",ans); } int main() { srand((unsigned)time(NULL)); init(); GA(); return 0; }
标签:
原文地址:http://www.cnblogs.com/XDJjy/p/5019855.html