标签:
knn算法:
1.优点:精度高、对异常值不敏感、无数据输入假定
2.缺点:计算复杂度高、空间复杂度高。
3.适用数据范围:数值型和标称型。
一般流程:
1.收集数据
2.准备数据
3.分析数据
4.训练算法:不适用
5.测试算法:计算正确率
6.使用算法:需要输入样本和结构化的输出结果,然后运行k-近邻算法判定输入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理。
2.1.1 导入数据
operator是排序时要用的
from numpy import * import operator def createDataSet(): group=array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]]) labels=[‘A‘,‘A‘,‘B‘,‘B‘] return group,labels
保存到knn.py文件
更改当前工作目录,导入knn
os.chdir(‘G:\\学习\\机器学习实战‘) import knn
调用knn,创建数据集
group,labels=knn.createDataSet()
2.1.2 实施knn算法
1.计算己知类别数据集中的点与当前点之间的距离
2.按照距离递增次数序排序
3.选取与当前点距离最小的k个点
4.确定前k个点所在类别的出现频率
5.返回前k个点出现频率最高的类别作为当前点的预测分类
4个参数:
a.inX:用于分类的输入向量
b.dataSet:训练样本
c.标签向量:labels
d.k:用于选择最近邻居的数目
def classify0(inX, dataSet, labels, k): dataSetSize = dataSet.shape[0] diffMat = tile(inX, (dataSetSize,1)) - dataSet sqDiffMat = diffMat**2 sqDistances = sqDiffMat.sum(axis=1) distances = sqDistances**0.5 sortedDistIndicies = distances.argsort() classCount={} for i in range(k): voteIlabel = labels[sortedDistIndicies[i]] classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0]
1~5行计算欧氏距离
6行按从小到大排序distances.argsort(),排完序后是下标
2.2 使用knn算法改进约会网站的配对效果
在knn.py中添加函数
strip是去掉前后的\n,[-1]竟然是指最后一列
def file2matrix(filename): fr = open(filename) numberOfLines = len(fr.readlines()) #get the number of lines in the file returnMat = zeros((numberOfLines,3)) #prepare matrix to return classLabelVector = [] #prepare labels return fr = open(filename) index = 0 for line in fr.readlines(): line = line.strip() listFromLine = line.split(‘\t‘) returnMat[index,:] = listFromLine[0:3] classLabelVector.append(listFromLine[-1]) index += 1 return returnMat,classLabelVector
重新加载一下knn,并调用函数
reload(knn) datingDataMat,datingLabels=knn.file2matrix(‘datingTestSet.txt‘)
2.2.2 分析数据:使用Matplotlib创建散点图
import matplotlib import matplotlib.pyplot as plt fig=plt.figure() ax=fig.add_subplot(111) ax.scatter(datingDataMat[:,1],datingDataMat[:,2]) plt.show()
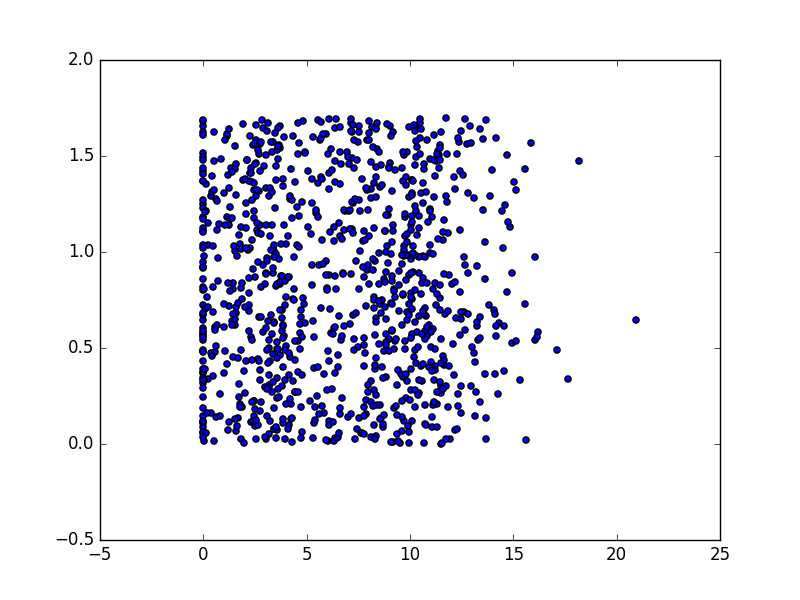
换一下,用颜色显示不同类别
import matplotlib import matplotlib.pyplot as plt fig=plt.figure() ax=fig.add_subplot(111) ax.scatter(datingDataMat[:,1],datingDataMat[:,2],15.0*numpy.array(datingLabels),15.0*numpy.array(datingLabels)) plt.show()
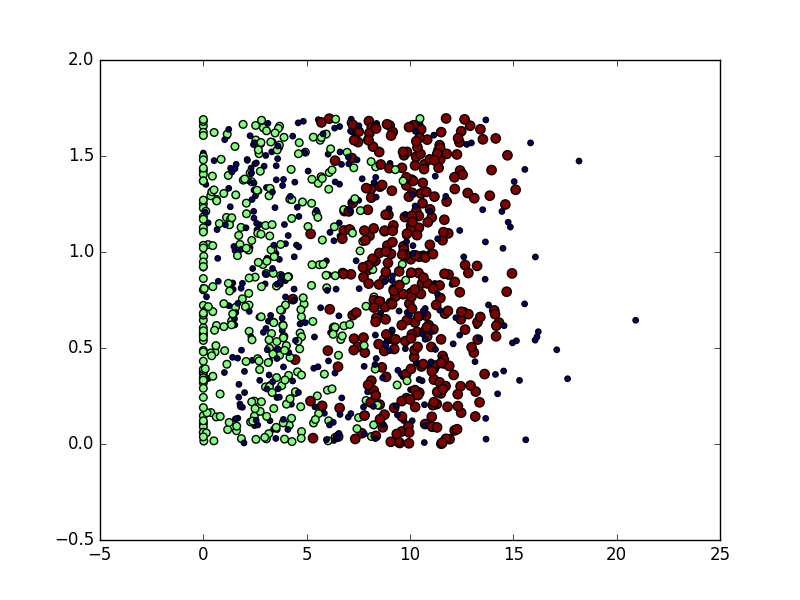
2.2.3 准备数据:归一化数值
def autoNorm(dataSet): minVals = dataSet.min(0) maxVals = dataSet.max(0) ranges = maxVals - minVals normDataSet = zeros(shape(dataSet)) m = dataSet.shape[0] normDataSet = dataSet - tile(minVals, (m,1)) normDataSet = normDataSet/tile(ranges, (m,1)) #element wise divide return normDataSet, ranges, minVals
2.2.4 作为完整程序验证分类器
def datingClassTest(): hoRatio = 0.50 #hold out 10% datingDataMat,datingLabels = file2matrix(‘datingTestSet2.txt‘) #load data setfrom file normMat, ranges, minVals = autoNorm(datingDataMat) m = normMat.shape[0] numTestVecs = int(m*hoRatio) errorCount = 0.0 for i in range(numTestVecs): classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3) print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]) if (classifierResult != datingLabels[i]): errorCount += 1.0 print "the total error rate is: %f" % (errorCount/float(numTestVecs)) print errorCount
标签:
原文地址:http://www.cnblogs.com/MarsMercury/p/5020405.html