深度优先搜索与广度优先搜索算法理解

标签：

深度优先搜索算法和广度优先搜索算法是图论中两个有意思也很实用的算法，下面我们来看看这两个算法。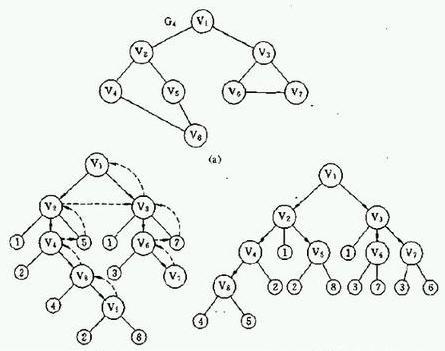

严书中，给出的利用深度优先搜索(Deep First Search)算法进行图的遍历伪码如下 

 1 Boolean visited[MAX]; //标志数组 
 2 Status (*VisitFunction)(int v); //访问函数
 3  
 4 void DFSTraverse(Graph G, Status (*Visit)(int v))
 5 {
 6     VisitFunction = Visit;
 7     for(v = 0; v < G.vexnum; ++v) //初始化标志数组
 8         visited[v] = false;
 9     for(v = 0; v < G.vexnum; ++v) //对未访问过的顶点调用DFS
10         if(!visited[v])
11             DFS(G, v);
12 }
13  
14 void DFS(Graph G, int v) //从顶点v出发进行DFS
15 {
16     visited[v] = true;
17     VisitFunction(v);
18     for(w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w))
19         if(!visited[w])
20             DFS(G, w); //递归调用未访问的邻接顶点w
21 }    

进行深度优先搜索和广度优先搜索需要记录顶点访问情况，因为图中的环会对遍历图造成麻烦。要解决此问题可以使用一个初始值为false的visited数组，其下标为顶点在相应的存储结构中的对应下标，当一个顶点被访问后，visited数组中其对应的值变为true。在上面给出的算法中第9行代码是为了解决在非连通图中会出现的对一个顶点进行深度优先搜索不完全的情况。14行开始的深度优先搜索算法基于递归，对于传入的图G以及一个顶点v，当w = FirstAdjVex(G, v)得到的顶点w的visited情况为false时会一直访问FirstAdjVex，而当遇到visited[w] = false的情况则表明从顶点v开始每次从FirstAdjVex获得顶点形成的路径已经搜索完毕，随着弹出栈，上一级的NextAdjVex开始搜寻下一个邻接顶点，重复这个过程，最后v所在连通图就能够被深度优先遍历。

对应与上面的图，由于其是连通图，只要关注DFS算法部分就可以。当传入参数是G和v1时，首先标记v1的visited情况为true（以后简称v1为true，false同理)，访问v1，v1的FirstAdjVex为v2，因此w = v2，由于v2为false，调用DFS本身，标记v2为true，访问v2，接下来v4, v8, v5同理，而v5的FirstAdjVex为v2，v2已被访问过visited值为true，w试图获取v5的NextAdjVex，但v5并无NextAdjVex，本次调用结束，返回上一层，同理一直返回到v2，v2有NextAdjVex v5，但其已被访问过，而v2无下一NextAdjVex，继续返回到v1，v1的NextAdjVex为v3，可以访问，v3的FirstAdjVex v6可以访问，同理一直访问到v7，此时v7和此前v5状况一样，于是一直返回，v1返回后整个DFS函数结束。

DFS顺序v1 v2 v4 v8 v5 v3 v6 v7。

严书中的广度优先遍历算法伪码如下：

 1 void BFSTraverse(Graph G, Status (*Visit)(int v))
 2 {
 3     for(v = 0; v < G.vexnum; ++v)
 4         visited[v] = false;   
 5     InitQueue(Q);
 6     for(v = 0; v < G.vexnum; ++v)
 7         if(!visited[v])
 8         {
 9             visited[v] = true;
10             Visit(v);
11             EnQueue(Q, v);
12             while(!QueueEmpty(Q))
13             {
14                 DeQueue(Q, u);
15                 for(w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w))
16                     if(!visited[w])
17                     {
18                         visited[w] = true;
19                         visit(w);
20                         EnQueue(Q, w);
21                     }
22             }
23         }
24 }

为了实现广度优先搜索，利用了队列这一数据结构，第6行的for循环是为了处理非联通图，我们以顶部的图为例，该循环只会经历一次。以v1开始这个循环，首先标记v1为true，访问v1，再入队列，此时队列元素为<v1>，Q不为空，出队列，并将队列元素赋值给u，这部后队列为<>，接下来的for循环以u的FirstAdjVex即v2开始，标记v2，访问v2，将v2入队列，此时队列为<v2>，回到15行的for循环，u的NextAdjVex即v3被赋值给w，同样的，标记v3，访问v3，v3入队列，此时队列<v2, v3>， 之后再回到15行，而v1此时无NextAdjVex，返回12行，队列不空，v2出队列赋给u，此时队列<v3>，与之前同样的，标记并访问入队列v4，标记并访问入队列v5，返回12行，此时队列<v3, v4, v5>，v3出队列赋给u，依次标记并访问入队列v6，v7，再回到12行，队列为<v4, v5, v6, v7>，v4出队列，标记并访问入队列v8，返回12行，此时队列<v5, v6, v7, v8>，v5出队列赋值给u，由于v5的AdjVex v8已被访问，回到12行，同理v6, v7, v8出队列，最后队列为空，函数结束。

BFS顺序v1 v2 v3 v4 v5 v6 v7 v8

深度优先搜索与广度优先搜索算法理解

标签：

原文地址：http://www.cnblogs.com/rafacheng/p/5024582.html