标签:
同进化算法(见博客《[Evolutionary Algorithm] 进化算法简介》,进化算法是受生物进化机制启发而产生的一系列算法)和人工神经网络算法(Neural Networks,简称NN,神经网络是从信息处理角度对人脑的神经元网络系统进行了模拟的相关算法)一样,群体智能优化算法也属于一种生物启发式方法,它们三者可以称为是人工智能领域的三驾马车(PS:实际上除了上述三种算法还有一些智能算法应用也很广泛,比如模拟金属物质热力学退火过程的模拟退火算法(Simulated Algorithm,简称SA),模拟人体免疫系统在抗原刺激下产生抗体过程的人工免疫系统算法(Artificial Immune System,简称AIS)等,但是相对三者而言,模拟退火和人工免疫系统算法已逐渐处于低潮期)。群体智能优化算法主要模拟了昆虫、兽群、鸟群和鱼群的群集行为,这些群体按照一种合作的方式寻找食物,群体中的每个成员通过学习它自身的经验和其他成员的经验来不断地改变搜索的方向。群体智能优化算法的突出特点就是利用了种群的群体智慧进行协同搜索,从而在解空间内找到最优解。

常见的群体智能优化算法主要有如下几类:
(1)蚁群算法(Ant Colony Optimization,简称ACO)[1992年提出];
(2)粒子群优化算法(Particle Swarm Optimization,简称PSO)[1995年提出](简单易于实现,也是目前应用最为广泛的群体智能优化算法);
(3)菌群优化算法(Bacterial Foraging Optimization,简称BFO)[2002年提出];
(4)蛙跳算法(Shuffled Frog Leading Algorithm,简称SFLA)[2003年提出];
(5)人工蜂群算法(Artificial Bee Colony Algorithm,简称ABC)[2005年提出];
除了上述几种常见的群体智能算法以外,还有一些并不是广泛应用的群体智能算法,比如萤火虫算法、布谷鸟算法、蝙蝠算法以及磷虾群算法等等。
由于博主对粒子群优化算法比较熟悉,在硕士期间也进行了比较系统的学习,所以利用本博文系统的介绍一下应用最为广泛的PSO算法。
粒子群优化算法是在1995年由Eberhart博士和Kennedy博士一起提出的,它源于对鸟群捕食行为的研究。它的基本核心是利用群体中的个体对信息的共享从而使得整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的最优解。我们可以利用一个有关PSO的经典描述来对PSO算法进行一个直观的描述。设想这么一个场景:一群鸟进行觅食,而远处有一片玉米地,所有的鸟都不知道玉米地到底在哪里,但是它们知道自己当前的位置距离玉米地有多远。那么找到玉米地的最佳策略,也是最简单有效的策略就是是搜寻目前距离玉米地最近的鸟群的周围区域。PSO就是从这种群体觅食的行为中得到了启示,从而构建的一种优化模型。
在PSO中,每个优化问题的解都是搜索空间中的一只鸟,称之为“粒子”,而问题的最优解就对应为鸟群要寻找的“玉米地”。所有的粒子都具有一个位置向量(粒子在解空间的位置)和速度向量(决定下次飞行的方向和速度),并可以根据目标函数来计算当前的所在位置的适应值(fitness value),可以将其理解为距离“玉米地”的距离。在每次的迭代中,种群中的粒子除了根据自身的“经验”(历史位置)进行学习以外,还可以根据种群中最优粒子的“经验”来学习,从而确定下一次迭代时需要如何调整和改变飞行的方向和速度。就这样逐步迭代,最终整个种群的粒子就会逐步趋于最优解。
在介绍PSO的算法流程之前,我们写给出PSO中常用的迭代算子的形式。令Xi=(xi1,xi2,...,xin)代表粒子i的位置向量,Vi=(vi1,vi2,...,vin)代表粒子i的速度向量(其中n为优化问题的维度大小),最早版本的粒子群优化算法的迭代算子形式如下:
速度向量迭代公式:
Vi=Vi+c1r1(Pbesti−Xi)+c2r2(Gbest−Xi) (1)
位置向量迭代公式:
Xi=Xi+Vi (2)
其中在公式(1)中,Pbesti和Gbest分别代表粒子i的历史最佳位置向量和种群历史最佳位置向量。根据公式(1)(2)可以看出,种群中的粒子通过不断地向自身和种群的历史信息进行学习,从而可以找出问题的最优解。
但是,在后续的研究中表明,上述原始的公式中存在一个问题:公式(1)中Vi的更新太具有随机性,从而使得整个PSO算法的全局优化能力很强,但是局部搜索能力较差。而实际上,我们需要在算法迭代初期PSO有着较强的全局优化能力,而在算法的后期,整个种群应该具有更强的局部搜索能力。所以根据上述的弊端,Shi和Eberhart通过引入惯性权重修改了公式(1),从而提出了PSO的惯性权重模型:
速度向量迭代公式:
Vi=wVi+c1r1(Pbesti−Xi)+c2r2(Gbest−Xi) (3)
其中参数w称为是PSO的惯性权重(inertia weight),它的取值介于[0,1]区间,一般应用中均采取自适应的取值方法,即一开始令w=0.9,使得PSO全局优化能力较强,随着迭代的深入,参数w进行递减,从而使得PSO具有较强的局部优化能力,当迭代结束时,w=0.1。参数c1和c2称为是学习因子(learn factor),一般设置为1.4961;而r1和r2为介于[0,1]之间的随机概率值。
整个粒子群优化算法的算法框架如下:
Step 1 种群初始化:可以进行随机初始化或者根据被优化的问题设计特定的初始化方法,然后计算个体的适应值,从而选择出个体的局部最优位置向量Pbesti和种群的全局最优位置向量Gbest。
Step 2 迭代设置:设置迭代次数gmax,并令当前迭代次数g=1;
Step 3 速度更新:根据公式(3)更新每个个体的速度向量;
Step 4 位置更新:根据公式(2)更新每个个体的位置向量;
Step 5 局部位置向量和全局位置向量更新:更新每个个体的Pbesti和种群的Gbest;
Step 6 终止条件判断:判断迭代次数时都达到gmax,如果满足,输出Gbest;否则继续进行迭代,跳转至Step 3。
对于粒子群优化算法的运用,主要是对速度和位置向量迭代算子的设计。迭代算子是否有效将决定整个PSO算法性能的优劣,所以如何设计PSO的迭代算子是PSO算法应用的研究重点和难点。
参数w被称之为是惯性权重,顾名思义w实际反映了粒子过去的运动状态对当前行为的影响,就像是我们物理中提到的惯性。如果w<<1,从前的运动状态很少能影响当前的行为,粒子的速度会很快的改变;相反,w较大,虽然会有很大的搜索空间,但是粒子很难改变其运动方向,很难向较优位置收敛,由于算法速度的因素,在实际运用中很少这样设置。也就是说,较高的w设置促进全局搜索,较低的w设置促进快速的局部搜索。
旅行商问题(Traveling Salesman Problem,TSP)又译为旅行推销员问题、货郎担问题,简称为TSP问题,是最基本的路线问题和最典型的NP难问题,该问题是在寻求单一旅行者由起点出发,通过所有给定的需求点之后,最后再回到原点的最小路径成本。最早的旅行商问题的数学规划是由Dantzig等人于1959年提出的。
下面为一个TSP问题的数据集,城市个数为50:
1 37 52
2 49 49
3 52 64
4 20 26
5 40 30
6 21 47
7 17 63
8 31 62
9 52 33
10 51 21
11 42 41
12 31 32
13 5 25
14 12 42
15 36 16
16 52 41
17 27 23
18 17 33
19 13 13
20 57 58
21 62 42
22 42 57
23 16 57
24 8 52
25 7 38
26 27 68
27 30 48
28 43 67
29 58 48
30 58 27
31 37 69
32 38 46
33 46 10
34 61 33
35 62 63
36 63 69
37 32 22
38 45 35
39 59 15
40 5 6
41 10 17
42 21 10
43 5 64
44 30 15
45 39 10
46 32 39
47 25 32
48 25 55
49 48 28
50 56 37
51 30 40
50个城市分布图:
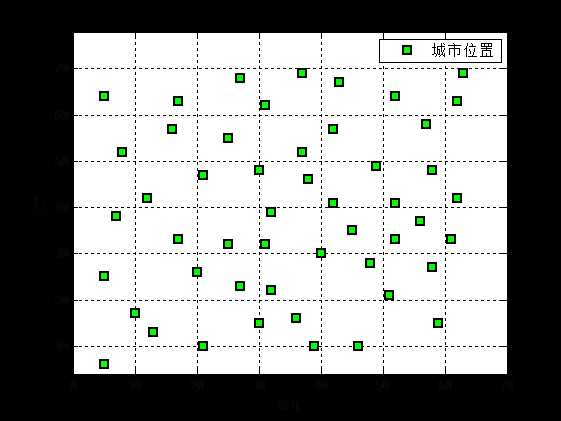
下面为PSO求解旅行商问题的matlab代码:
主函数main.m:
%% 该文件演示基于TSP-PSO算法
clc;clear
%% 载入数据
data=load(‘eil51.txt‘)
cityCoor=[data(:,2) data(:,3)];%城市坐标矩阵
figure
plot(cityCoor(:,1),cityCoor(:,2),‘ms‘,‘LineWidth‘,2,‘MarkerEdgeColor‘,‘k‘,‘MarkerFaceColor‘,‘g‘)
legend(‘城市位置‘)
ylim([4 78])
title(‘城市分布图‘,‘fontsize‘,12)
xlabel(‘km‘,‘fontsize‘,12)
ylabel(‘km‘,‘fontsize‘,12)
%ylim([min(cityCoor(:,2))-1 max(cityCoor(:,2))+1])
grid on
%% 计算城市间距离
n=size(cityCoor,1); %城市数目
cityDist=zeros(n,n); %城市距离矩阵
for i=1:n
for j=1:n
if i~=j
cityDist(i,j)=((cityCoor(i,1)-cityCoor(j,1))^2+...
(cityCoor(i,2)-cityCoor(j,2))^2)^0.5;
end
cityDist(j,i)=cityDist(i,j);
end
end
nMax=1000; %进化次数
indiNumber=50; %个体数目
individual=zeros(indiNumber,n);
%^初始化粒子位置
for i=1:indiNumber
individual(i,:)=randperm(n);
end
%% 计算种群适应度
indiFit=fitness(individual,cityCoor,cityDist);
[value,index]=min(indiFit);
tourPbest=individual; %当前个体最优
tourGbest=individual(index,:) ; %当前全局最优
recordPbest=inf*ones(1,indiNumber); %个体最优记录
recordGbest=indiFit(index); %群体最优记录
xnew1=individual;
%% 循环寻找最优路径
L_best=zeros(1,nMax);
for N=1:nMax
N
%计算适应度值
indiFit=fitness(individual,cityCoor,cityDist);
%更新当前最优和历史最优
for i=1:indiNumber
if indiFit(i)<recordPbest(i)
recordPbest(i)=indiFit(i);
tourPbest(i,:)=individual(i,:);
end
if indiFit(i)<recordGbest
recordGbest=indiFit(i);
tourGbest=individual(i,:);
end
end
[value,index]=min(recordPbest);
recordGbest(N)=recordPbest(index);
%% 交叉操作
for i=1:indiNumber
% 与个体最优进行交叉
c1=unidrnd(n-1); %产生交叉位
c2=unidrnd(n-1); %产生交叉位
while c1==c2
c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1;
end
chb1=min(c1,c2);
chb2=max(c1,c2);
cros=tourPbest(i,chb1:chb2);
ncros=size(cros,2);
%删除与交叉区域相同元素
for j=1:ncros
for k=1:n
if xnew1(i,k)==cros(j)
xnew1(i,k)=0;
for t=1:n-k
temp=xnew1(i,k+t-1);
xnew1(i,k+t-1)=xnew1(i,k+t);
xnew1(i,k+t)=temp;
end
end
end
end
%插入交叉区域
xnew1(i,n-ncros+1:n)=cros;
%新路径长度变短则接受
dist=0;
for j=1:n-1
dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
if indiFit(i)>dist
individual(i,:)=xnew1(i,:);
end
% 与全体最优进行交叉
c1=round(rand*(n-2))+1; %产生交叉位
c2=round(rand*(n-2))+1; %产生交叉位
while c1==c2
c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1;
end
chb1=min(c1,c2);
chb2=max(c1,c2);
cros=tourGbest(chb1:chb2);
ncros=size(cros,2);
%删除与交叉区域相同元素
for j=1:ncros
for k=1:n
if xnew1(i,k)==cros(j)
xnew1(i,k)=0;
for t=1:n-k
temp=xnew1(i,k+t-1);
xnew1(i,k+t-1)=xnew1(i,k+t);
xnew1(i,k+t)=temp;
end
end
end
end
%插入交叉区域
xnew1(i,n-ncros+1:n)=cros;
%新路径长度变短则接受
dist=0;
for j=1:n-1
dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
if indiFit(i)>dist
individual(i,:)=xnew1(i,:);
end
%% 变异操作
c1=round(rand*(n-1))+1; %产生变异位
c2=round(rand*(n-1))+1; %产生变异位
while c1==c2
c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1;
end
temp=xnew1(i,c1);
xnew1(i,c1)=xnew1(i,c2);
xnew1(i,c2)=temp;
%新路径长度变短则接受
dist=0;
for j=1:n-1
dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
if indiFit(i)>dist
individual(i,:)=xnew1(i,:);
end
end
[value,index]=min(indiFit);
L_best(N)=indiFit(index);
tourGbest=individual(index,:);
end
tourGbest
minbest=min(L_best)
%% 结果作图
figure
plot(L_best)
title(‘算法训练过程‘)
xlabel(‘迭代次数‘)
ylabel(‘适应度值‘)
grid on
figure
hold on
plot([cityCoor(tourGbest(1),1),cityCoor(tourGbest(n),1)],[cityCoor(tourGbest(1),2),...
cityCoor(tourGbest(n),2)],‘ms-‘,‘LineWidth‘,2,‘MarkerEdgeColor‘,‘k‘,‘MarkerFaceColor‘,‘g‘)
hold on
for i=2:n
plot([cityCoor(tourGbest(i-1),1),cityCoor(tourGbest(i),1)],[cityCoor(tourGbest(i-1),2),...
cityCoor(tourGbest(i),2)],‘ms-‘,‘LineWidth‘,2,‘MarkerEdgeColor‘,‘k‘,‘MarkerFaceColor‘,‘g‘)
hold on
end
legend(‘规划路径‘)
scatter(cityCoor(:,1),cityCoor(:,2));
title(‘规划路径‘,‘fontsize‘,10)
xlabel(‘km‘,‘fontsize‘,10)
ylabel(‘km‘,‘fontsize‘,10)
grid on
ylim([4 80])
目标函数:fitness.m
function indiFit=fitness(x,cityCoor,cityDist)
%% 该函数用于计算个体适应度值
%x input 个体
%cityCoor input 城市坐标
%cityDist input 城市距离
%indiFit output 个体适应度值
m=size(x,1);
n=size(cityCoor,1);
indiFit=zeros(m,1);
for i=1:m
for j=1:n-1
indiFit(i)=indiFit(i)+cityDist(x(i,j),x(i,j+1));
end
indiFit(i)=indiFit(i)+cityDist(x(i,1),x(i,n));
end
PSO迭代收敛曲线图:
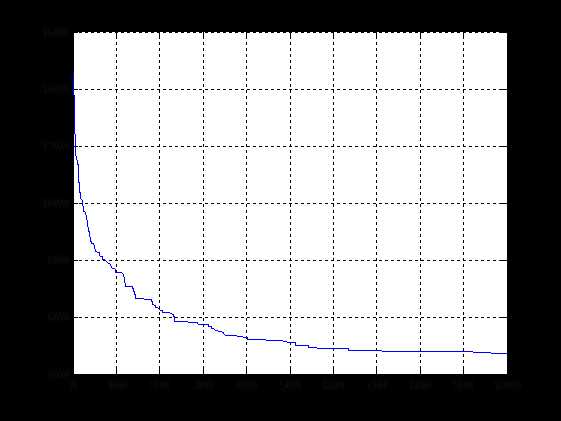
PSO求解50个城市的TSP问题最小距离为473.1536,TSP求解规划路径图如下:
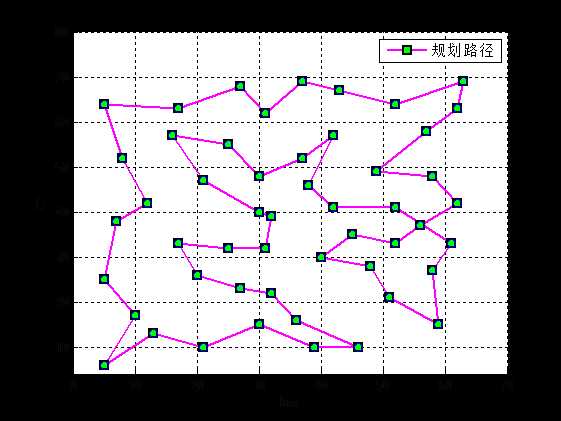
[1] Eberhart R C and Kennedy J. A new optimizer using particle swarm theory. 1995.
[2] Shi Y and Eberhart R C. A modified particle optimizer. 1998.
[3] Kennedy J. Particle swarm optimization. 2010.
标签:
原文地址:http://www.cnblogs.com/Leo_wl/p/5049732.html