数据结构之拓扑排序

标签：

转自:http://blog.csdn.net/dm_vincent/article/details/7714519

原理：该算法的实现十分直观，关键在于需要维护一个入度为0（没有入）的顶点的集合：

        每次从该集合中取出(没有特殊的取出规则，随机取出也行，使用队列/栈也行，下同)一个顶点，将该顶点放入保存结果的List中。

紧接着循环遍历由该顶点引出的所有边，从图中移除这条边，同时获取该边的另外一个顶点，如果该顶点的入度在减去本条边之后为0，那么也将这个顶点放到入度为0的集合中。然后继续从集合中取出一个顶点…………

    当集合为空之后，检查图中是否还存在任何边，如果存在的话，说明图中至少存在一条环路。不存在的话则返回结果List，此List中的顺序就是对图进行拓扑排序的结果。

例如：

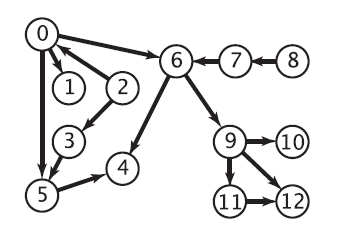
对上图进行拓扑排序的结果：

2->8->0->3->7->1->5->6->9->4->11->10->12

复杂度分析：

初始化入度为0的集合需要遍历整张图，检查每个节点和每条边，因此复杂度为O(E+V);

然后对该集合进行操作，又需要遍历整张图中的，每条边，复杂度也为O(E+V);

因此Kahn算法的复杂度即为O(E+V)。

个人理解：首先确定入读为0 的节点，去除该点和有关联的边，然后依次执行上步骤，当集合为空之后，检查图中是否还存在任何边，如果存在的话，说明图中至少存在一条环路。不存在的话则返回结果List，此List中的顺序就是对图进行拓扑排序的结果。

数据结构之拓扑排序

标签：

原文地址：http://www.cnblogs.com/neversayno/p/5062086.html