标签:
#01、引言,我们知道算式计算的问题是栈里面一个非常经典的题目。但是用栈来实现是一个非常麻烦的过程,第一要解决算式判断,是否为符合规则的算式,第二要由中最表达式转化为后缀表达式。这两个部分是栈实现计算算式表达式的比较复杂的地方。不仅如此,栈实现里面的各种运算符的优先级,各种条件判断,可以说是麻烦的要命。但是,实际上有一种数据结构比栈更适合解决这类问题。可以说是得天独厚的优势。对,就是二叉树。例如一个表达式:1+2*3-4/5
我们构造这样一个二叉树
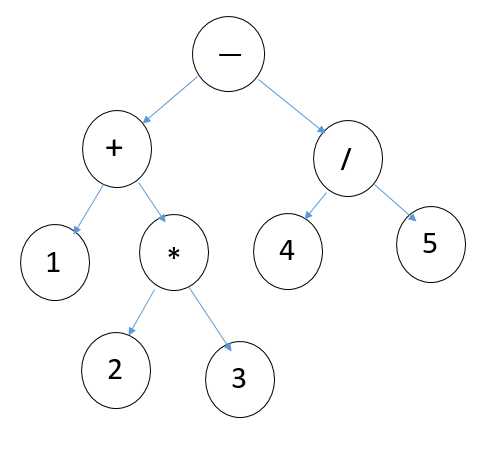
1 #define Maxsize 100 2 //定义数据元素类型 3 typedef char elemtype; 4 //定义二叉树数据变量 5 typedef union 6 { 7 char Operator; 8 double date; 9 }perdate; 10 //定义二叉树链式存储结构 11 typedef struct node 12 { 13 perdate DATE;//用union类型存运算符或操作数 14 struct node *lchild; 15 struct node *rchild; 16 }btnode;
1 struct op 2 { 3 char opration; 4 int index;//括号层数//当这个index被标记为-1时,就不会再次被查找到 5 int locate;//op的位置 6 };
用union定义一个perdate类型,用来分别记录操作数和运算符。op是查找运算符时用,从后往前查找,括号级数最低的作为根节点来创建二叉树。
0x002、实现的函数
//查找op,并填充Aop数组 int Sortop(char str[], op Aop[], int &index); //将字符串转化为浮点数 double str_to_flaot(char strpoly[], int p,int q); //判断数组是不是1.2类型,就是只有数据 bool isdate(char str[],int p,int q);//p,q指向str的开始和结尾处 //判断str是否为运算符和括号 bool isoprater(char str[],int p,int q);//p,q指向str的开始和结尾处 //用算数表达式创建二叉树 void Createbtnode(btnode *b, char *str, int p, int q,int tail);//p,q指向str的开始和结尾处;tail是Aop的尾指针 //计算二叉树算式的结果 double Comp(btnode *b);
0x003、main函数,整个算法过程简述
#include"标头.h" int index = 0;//记录最大的括号层数 struct op Aop[Maxsize];
1 int main() 2 { 3 btnode * b; 4 b = new btnode; 5 char str[Maxsize]; 6 cout << "算式计算器[张安源]" << endl; 7 while(true) 8 { 9 cout << "[Type \"exit\" to exit]" << endl << "请输入你要求的表达式:" << endl; 10 cin.getline(str, Maxsize); 11 if (strcmp("exit", str) == 0) break;//如果输入的是exit则退出 12 else 13 { 14 int tail = Sortop(str, Aop, index);//整理得到Aop的结构数组 15 Createbtnode(b, str, 0, strlen(str) - 1, tail); 16 double result = Comp(b); 17 cout << result << endl; 18 } 19 } 20 }
一直循环,让用户输入一个表达式,当输入为exit时,退出循环。Sortop函数将表达式的操作符的括号层数和其在表达式的位置经行记录到Aop数组里面,返回值是最大的括号层数。然后由Createbtnode函数创建一个二叉树b。comp求出二叉树表达式的结构,然后输出结果。大致的过程是这样,但是里面却还包含了一些实现的细节,具体代码是怎么实现的就不啰嗦了,看代码比讲解跟方便。
0x004、整个project。
<1>Header.h
1 #pragma once 2 #include<iostream> 3 using namespace std; 4 #define Maxsize 100 5 //定义数据元素类型 6 //*********int check = 0;//作为判断表达式是否正确的标记 7 typedef char elemtype; 8 //定义二叉树数据变量 9 typedef union 10 { 11 char Operator; 12 double date; 13 }perdate; 14 //定义二叉树链式存储结构 15 typedef struct node 16 { 17 perdate DATE;//用union类型存运算符或操作数 18 struct node *lchild; 19 struct node *rchild; 20 }btnode; 21 //定义查找运算符的结构数组 22 struct op 23 { 24 char opration; 25 int index;//括号层数//当这个index被标记为-1时,就不会再次被查找到 26 int locate;//op的位置 27 }; 28 extern int index; 29 extern struct op Aop[Maxsize]; 30 //****************************************************** 31 //查找op,并填充Aop数组 32 int Sortop(char str[], op Aop[], int &index); 33 //将字符串转化为浮点数 34 double str_to_flaot(char strpoly[], int p,int q); 35 //判断数组是不是1.2类型,就是只有数据 36 bool isdate(char str[],int p,int q);//p,q指向str的开始和结尾处 37 //判断str是否为运算符和括号 38 bool isoprater(char str[],int p,int q);//p,q指向str的开始和结尾处 39 //用算数表达式创建二叉树 40 void Createbtnode(btnode *b, char *str, int p, int q,int tail);//p,q指向str的开始和结尾处;tail是Aop的尾指针 41 //计算二叉树算式的结果 42 double Comp(btnode *b);
<2>op.cpp
1 #include"标头.h" 2 //查找op,并填充Aop数组 3 int Sortop(char str[], op Aop[], int &index) 4 { 5 int j = 0;//记录Aop的top 6 int i; 7 int ind = 0;//记录括号层数 8 for (i = 0; str[i] != ‘\0‘; i++) 9 { 10 if (str[i] == ‘(‘) 11 ind++; 12 else if (str[i] == ‘)‘) 13 ind--; 14 else if (str[i] == ‘+‘ || str[i] == ‘-‘ || str[i] == ‘*‘||str[i]==‘/‘ || str[i] == ‘^‘) 15 { 16 Aop[j].opration = str[i]; 17 Aop[j].index = ind; 18 Aop[j].locate = i; 19 j++; 20 } 21 index = (index > ind) ? index : ind; 22 } 23 return j; 24 } 25 //将字符串转化为浮点数 26 double str_to_flaot(char strpoly[], int p,int q) 27 { 28 if (strpoly[p] == ‘(‘) 29 p++; 30 if (strpoly[q] == ‘)‘) 31 q--; 32 //判断小数点前有几位数字 33 int index = 0; 34 int temp = p;//保存原来的p值 35 double n = 0;//最后的浮点数 36 for (;( p <= q)&&(strpoly[p]!=‘.‘); p++) index++; 37 p = temp; 38 for (; p<=q; p++) 39 { 40 if (strpoly[p] == ‘.‘) continue; 41 index--; 42 n = n + ((double)(strpoly[p] - ‘0‘))*(pow(10, index)); 43 44 } 45 return n; 46 } 47 //判断数组是不是1.2类型,就是只有数据//忽略括号 48 bool isdate(char str[],int p,int q) 49 { 50 int i; 51 int index = 0; 52 for (i = p; i<=q; i++) 53 { 54 if (str[i] == ‘.‘) 55 index++; 56 if (str[i] == ‘+‘ || str[i] == ‘-‘ || str[i] == ‘*‘ ||str[i]==‘/‘ || str[i] == ‘^‘) 57 return false; 58 } 59 if (index== 0 || index == 1) 60 { 61 return true; 62 } 63 else 64 abort(); 65 } 66 //判断str是否为运算符和括号 67 bool isoprater(char str[],int p,int q) 68 { 69 if ((p==q)&&(str[p] == ‘(‘ || str[p] == ‘)‘ || str[p] == ‘*‘||str[p]==‘/‘ || str[p] == ‘^‘ || str[p] == ‘+‘ || str[p] == ‘-‘)) 70 return true; 71 else 72 return false; 73 } 74 //用算数表达式创建二叉树 75 void Createbtnode(btnode *b, char *str, int p, int q,int tail) //由str串创建二叉链 76 { //p,q分别标志Aop的首尾 77 int i = 0; 78 int j = 0;// 79 int find=0; 80 if (isdate(str,p,q))//str为1.3类型 81 { 82 //创建头节点,并将数据位置为str_to_double 83 b->DATE.date = str_to_flaot(str,p,q); 84 b->lchild = NULL; 85 b->rchild = NULL; 86 } 87 else if (isoprater(str,p,q))//str为+、—、^、(、)、* 88 { 89 abort(); 90 b->DATE.Operator = str[i]; 91 b->lchild = NULL; 92 b->rchild = NULL; 93 } 94 ///*************************************************************** 95 else 96 for (int temp = 0; temp <= index; temp++) 97 { 98 for (j = tail; j >=0; j--)//从后往前找,才符合运算的法则,前面先算后面后算 99 { 100 if (Aop[j].index == temp && ((Aop[j].opration == ‘+‘)||(Aop[j].opration == ‘-‘)) && Aop[j].locate >= p&&Aop[j].locate <= q) 101 { 102 find++; 103 Aop[j].index = -1;//标志这个已经被找过了 104 btnode *lt, *rt; 105 lt = new btnode; 106 rt = new btnode; 107 b->lchild = lt; 108 b->rchild = rt; 109 b->DATE.Operator = Aop[j].opration; 110 Createbtnode(b->lchild, str, p, Aop[j].locate - 1,tail); 111 Createbtnode(b->rchild, str, Aop[j].locate+1, q,tail); 112 } 113 } 114 if(find==0) 115 for (j = tail; j >=0; j--) 116 { 117 if (Aop[j].index == temp && ((Aop[j].opration == ‘*‘)||(Aop[j].opration==‘/‘)) && Aop[j].locate >= p&&Aop[j].locate <= q) 118 { 119 find++; 120 Aop[j].index = -1;//标志这个已经被找过了 121 btnode *lt, *rt; 122 lt = new btnode; 123 rt = new btnode; 124 b->lchild = lt; 125 b->rchild = rt; 126 b->DATE.Operator = Aop[j].opration; 127 Createbtnode(b->lchild, str, p, Aop[j].locate - 1,tail); 128 Createbtnode(b->rchild, str, Aop[j].locate+1, q,tail); 129 } 130 } 131 if(find==0) 132 for (j = tail; j >=0; j--) 133 { 134 if (Aop[j].index == temp && (Aop[j].opration == ‘^‘) && Aop[j].locate >= p&&Aop[j].locate <= q) 135 { 136 Aop[j].index = -1;//标志这个已经被找过了 137 btnode *lt, *rt; 138 lt = new btnode; 139 rt = new btnode; 140 b->lchild = lt; 141 b->rchild = rt; 142 b->DATE.Operator = Aop[j].opration; 143 Createbtnode(b->lchild, str, p, Aop[j].locate - 1,tail); 144 Createbtnode(b->rchild, str, Aop[j].locate+1, q,tail); 145 } 146 } 147 } 148 } 149 //计算二叉树算式的结果 150 double Comp(btnode *b) 151 { 152 double v1, v2; 153 if (b == NULL) return 0; 154 if (b->lchild == NULL && b->rchild == NULL) 155 return b->DATE.date; //叶子节点直接返回节点值 156 v1 = Comp(b->lchild); 157 v2 = Comp(b->rchild); 158 switch (b->DATE.Operator) 159 { 160 case ‘+‘: 161 return v1 + v2; 162 case ‘-‘: 163 return v1 - v2; 164 case ‘*‘: 165 return v1*v2; 166 case ‘/‘: 167 if (v2 != 0) 168 return v1 / v2; 169 else 170 abort(); 171 case ‘^‘: 172 return (pow(v1, v2)); 173 default: 174 abort(); 175 } 176 }
<3>main.h
1 #include"标头.h" 2 int index = 0;//记录最大的括号层数 3 struct op Aop[Maxsize]; 4 int main() 5 { 6 btnode * b; 7 b = new btnode; 8 char str[Maxsize]; 9 cout << "算式计算器[张安源]" << endl; 10 while(true) 11 { 12 cout << "[Type \"exit\" to exit]" << endl << "请输入你要求的表达式:" << endl; 13 cin.getline(str, Maxsize); 14 if (strcmp("exit", str) == 0) break;//如果输入的是exit则退出 15 else 16 { 17 int tail = Sortop(str, Aop, index);//整理得到Aop的结构数组 18 Createbtnode(b, str, 0, strlen(str) - 1, tail); 19 double result = Comp(b); 20 cout << result << endl; 21 } 22 } 23 }
#04算法测试
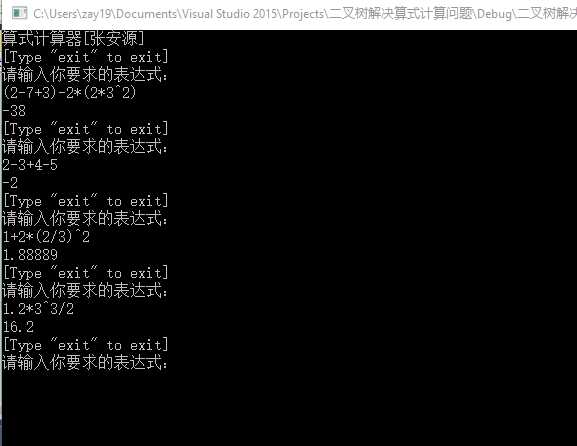
当输入的表达式符合规则时,返回表达式的值。
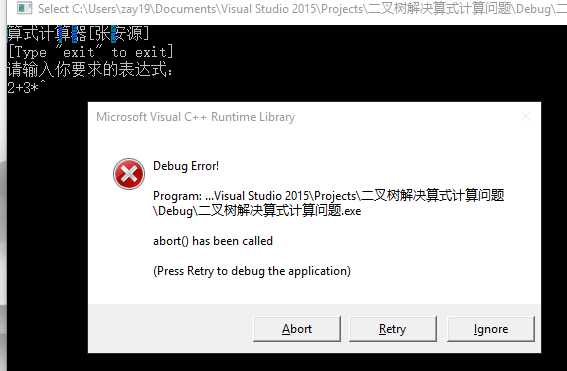
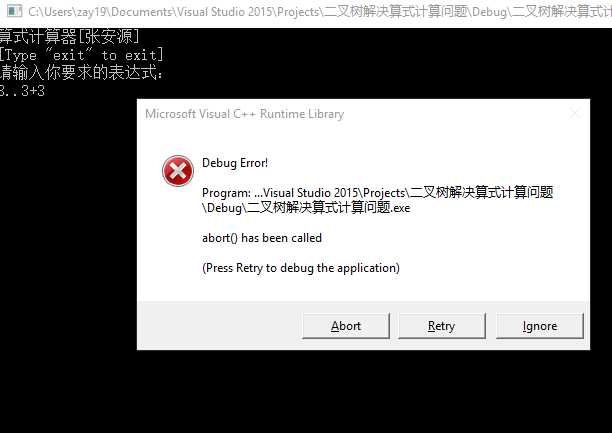
当输入的表达式不符合规则时,则调用abort函数。
#05、总结
好的数据结构能事半功倍,要培养善于发现的思维,当有某个思路然后去实现它,另外要积累经验。好好理解数据结构!
巧妙地用二叉树完成算式计算算法<计算器,二叉树,C++,独辟蹊径>
标签:
原文地址:http://www.cnblogs.com/ruxiaobai/p/5075526.html