标签:
这一章可能是Andrew Ng讲得最不清楚的一章,为什么这么说呢?这一章主要讲后向传播(Backpropagration, BP)算法,Ng花了一大半的时间在讲如何计算误差项$\delta$,如何计算$\Delta$的矩阵,以及如何用Matlab去实现后向传播,然而最关键的问题——为什么要这么计算?前面计算的这些量到底代表着什么,Ng基本没有讲解,也没有给出数学的推导的例子。所以这次内容我不打算照着公开课的内容去写,在查阅了许多资料后,我想先从一个简单的神经网络的梯度推导入手,理解后向传播算法的基本工作原理以及每个符号代表的实际意义,然后再按照课程的给出BP计算的具体步骤,这样更有助于理解。
FP算法还是很简单的,说白了就是根据前一层神经元的值,先加权然后取sigmoid函数得到后一层神经元的值,写成数学的形式就是:
$$a^{(1)}=X$$
$$z^{(2)}=\Theta^{(1)}a^{(1)}$$
$$a^{(2)}=g(z^{(2)})$$
$$z^{(3)}=\Theta^{(2)}a^{(2)}$$
$$a^{(3)}=g(z^{(3)})$$
$$z^{(4)}=\Theta^{(3)}a^{(3)}$$
$$a^{(4)}=g(z^{(4)})$$
$J(\Theta) = -\frac{1}{m}\left[\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{K}y^{(i)}_{k}log(h_\theta(x^{(i)}))_k + (1-y^{(i)}_k)log(1-(h_\theta(x^{(i)}))_k)\right]$
BP算法解决了什么问题?我们已经有了代价函数$J(\Theta)$,接下来我们需要利用梯度下降算法(或者其他高级优化算法)对$J(\Theta)$进行优化从而得到训练参数$\Theta$,然而关键问题是,优化算法需要传递两个重要的参数,一个代价函数$J(\Theta)$,另一个是代价函数的梯度$\frac{\partial J(\Theta)}{\partial \Theta}$,BP算法其实就是解决如何计算梯度的问题。
下面我们从一个简单的例子入手考虑如何从数学上计算代价函数的梯度,考虑如下简单的神经网络(为方便起见,途中已经给出了前向传播(FP)的计算过程),该神经网络有三层神经元,对应的有两个权重矩阵$\Theta^{(1)}$和$\Theta^{(2)}$,为计算梯度我们只需要计算两个偏导数即可:$\frac{\partial J(\Theta)}{\partial\Theta^{(1)}}$和$\frac{\partial J(\Theta)}{\partial\Theta^{(2)}}$。
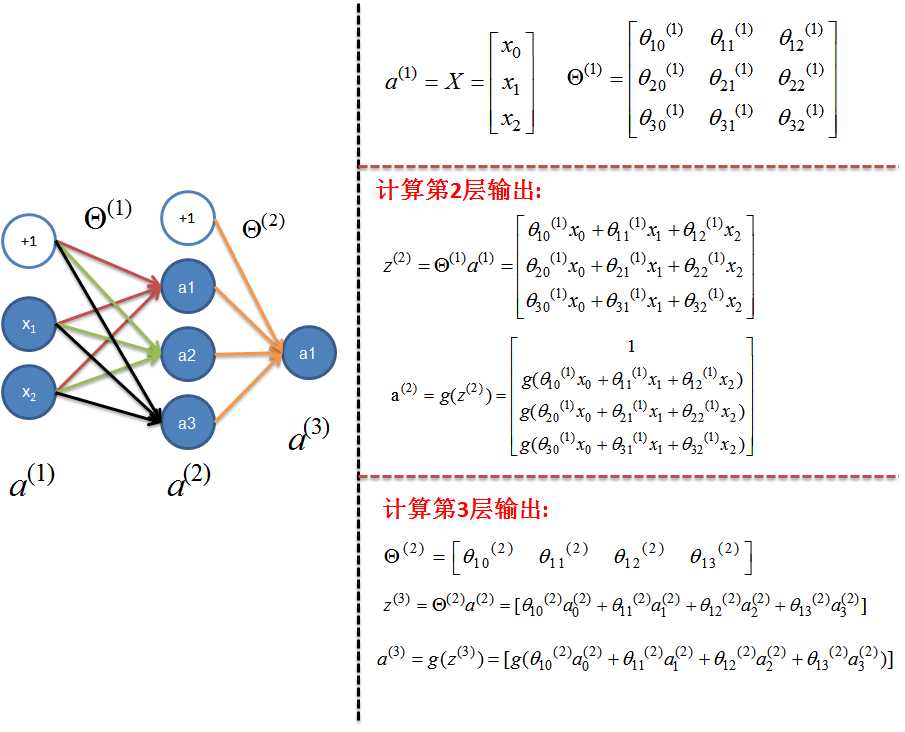
首先我们先计算第2个权重矩阵的偏导数,即$\frac{\partial}{\partial\Theta^{(2)}}J(\Theta)$。首先我们需要在$J(\Theta)$和$\Theta^{(2)}$之间建立联系,很容易可以看到$J(\Theta)$的值取决于$h_\theta(x)$,而$h_\theta(x)=a^{(3)}$, $a^{3}$又是由$z^{(3)}$取sigmoid得到,最后$z^{(3)}=\Theta^{(2)}\times a^{(2)}$,所以他们之间的联系可以如下表示:
![]()
按照求导的链式法则,我们可以先求$J(\Theta)$对$z^{(3)}$的导数,然后乘以$z^{(3)}$对$\Theta^{(2)}$的导数,即
$$\frac{\partial}{\partial\Theta^{(2)}}J(\Theta) = \frac{\partial}{\partial z^{(3)}}J(\Theta) \times \frac{\partial z^{(3)}}{\partial \Theta^{(2)}} $$
由$z^{(3)}=\Theta^{(2)}a^{(2)}$不难计算$\frac{\partial z^{(3)}}{\partial \Theta^{(2)}}=(a^{(2)})^T$,令$\frac{\partial}{\partial z^{(3)}}J(\Theta)=\delta^{(3)}$,上式可以重写为
$$\frac{\partial}{\partial\Theta^{(2)}}J(\Theta) =\delta^{(3)} (a^{(2)})^T$$
接下来仅需要计算$\delta^{(3)}$即可,由上一章的内容我们已经知道$g‘(z)=g(z)(1-g(z))$, $h_\theta(x)=a^{(3)}=g(z^{(3)})$,忽略前面的$1/m\sum\limits_{i=1}^{m}$(这里我们只对一个example推导,最后累加即可)
$$\begin{aligned}\delta^{(3)}&=\frac{\partial J(\Theta)}{z^{(3)}}\\&= (-y)\frac{1}{g(z^{(3)})}g^{‘}(z^{(3)})-(1-y)\frac{1}{1-g(z^{(3)})} [1-g(z^{(3)})]‘\\&=-y(1-g(z^{(3)}))+(1-y)g(z^{(3)})\\&=-y+g(z^{(3)})\\&=-y+a^{(3)}\end{aligned}$$
至此我们已经得到$J(\Theta)$对$\Theta^{(2)}$的偏导数,即
$$\frac{\partial J(\Theta)}{\partial\Theta^{(2)}}=(a^{(2)})^T\delta^{(3)}$$
$$\delta^{(3)}=a^{(3)}-y$$
接下来我们需要求$J(\Theta)$对$\Theta^{(1)}$的偏导数,$J(\Theta)$对$\Theta^{(1)}$的依赖关系如下:
![]()
根据链式求导法则有
$$\begin{aligned}\frac{\partial J(\Theta)}{\partial \Theta^{(1)}} &= \frac{\partial J(\Theta)}{\partial z^{(3)}} \frac{\partial z^{(3)}}{\partial a^{(2)}} \frac{\partial a^{(2)}}{\partial \Theta^{(1)}} \end{aligned}$$
我们分别计算等式右边的三项可得:
$$ \frac{\partial J(\Theta)}{\partial z^{(3)}}=\delta^{(3)}$$
$$\frac{\partial z^{(3)}}{\partial a^{(2)}}=(\Theta^{(2)})^T$$
$$\frac{\partial a^{(2)}}{\partial \Theta^{(1)}}=\frac{\partial a^{(2)}}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial \Theta^{(1)}}=g‘(z^{(2)}) a^{(1)}$$
带入后得
$$\frac{\partial J(\Theta)}{\partial \Theta^{(1)}}=(a^{(1)})^T \delta^{(3)} (\Theta^{(2)})^T g‘(z^{(2)})$$
令$\delta^{(2)}=\delta^{(3)} (\Theta^{(2)})^Tg‘(z^{(2)})$, 上式可以重写为
$$\frac{\partial J(\Theta)}{\partial \Theta^{(1)}}=(a^{(1)})^T \delta^{(2)}$$
$$\delta^{(2)}=\delta^{(3)} (\Theta^{(2)})^T g‘(z^{(2)})$$
把上面的结果放在一起,我们得到$J(\Theta)$对两个权重矩阵的偏导数为:
$$\delta^{(3)}=a^{(3)}-y$$
$$\frac{\partial J(\Theta)}{\partial\Theta^{(2)}}=(a^{(2)})^T\delta^{(3)}$$
$$\delta^{(2)}=\delta^{(3)} (\Theta^{(2)})^T g‘(z^{(2)})$$
$$\frac{\partial J(\Theta)}{\partial \Theta^{(1)}}=(a^{(1)})^T \delta^{(2)}$$
观察上面的四个等式,我们发现
所以可以从后往前逐层计算误差向量(这就是后向传播的来源),然后通过简单的乘法运算得到代价函数对每一层权重矩阵的偏导数。到这里算是终于明白为什么要计算误差向量,以及为什么误差向量之间有递归关系了。尽管这里的神经网络十分简单,推导过程也不是十分严谨,但是通过这个简单的例子,基本能够理解后向传播算法的工作原理了。
假设我们有$m$个训练example,$L$层神经网络,并且此处考虑正则项,即
$J(\Theta) = -\frac{1}{m}\left[\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{K}y^{(i)}_{k}log(h_\theta(x^{(i)}))_k + (1-y^{(i)}_k)log(1-(h_\theta(x^{(i)}))_k)\right] + \frac{\lambda}{2m}\sum\limits_{l=1}^{L-1}\sum\limits_{i=1}^{s_l}\sum\limits_{j=1}^{s_{l+1}}(\Theta_{ji}^{(l)})^2$
初始化:设置$\Delta^{(l)}_{ij}=0$ (理解为对第$l$层的权重矩阵的偏导累加值)
For i = 1 : m
end // for
计算梯度:
$$D_{ij}^{(l)}=\frac{1}{m}\Delta^{(l)}_{ij}, j=0$$
$$D_{ij}^{(l)}=\frac{1}{m}\Delta^{(l)}_{ij}+\lambda\Theta_{ij}^{(l)}, j\neq 0$$
$$\frac{\partial J(\Theta)}{\partial \Theta^{(l)}}=D^{(l)}$$
对于四层三个权重矩阵参数$\Theta^{(1)}, \Theta^{(2)}, \Theta^{(3)}$将其展开成一个参数向量,Matlab code如下:
thetaVec = [Theta1(:); Theta2(:); Theta3(:)];
为了保证梯度计算的正确性,可以用数值解进行检查,根据导数的定义
$$\frac{dJ(\theta)}{d\theta} \approx \frac{J(\theta + \epsilon)-J(\theta-\epsilon)}{2\epsilon}$$
Matlab Code 如下
for i = 1 : n
thetaPlus = theta;
thetaPlus(i) = thetaPlus(i) + EPS;
thetaMinus = theta;
thetaMinus(i) = thetaMinus(i) - EPS;
gradApprox(i) = (J(thetaPlus) - J(thetaMinus)) / (2 * EPS);
end
最后检查 gradApprox 是否约等于之前计算的梯度值即可。需要注意的是:因为近似的梯度计算代价很大,在梯度检查后记得关闭梯度检查的代码。
初始权重矩阵的初始化应该打破对称性 (symmetry breaking),避免使用全零矩阵进行初始化。可以采用随机数进行初始化,即 $\Theta^{(l)}_{ij} \in [-\epsilon, +\epsilon]$
[1] Andrew Ng Coursera 公开课第五周
[2] Derivation of Backpropagation. http://web.cs.swarthmore.edu/~meeden/cs81/s10/BackPropDeriv.pdf
[3] Wikipedia: Backpropagation. https://en.wikipedia.org/wiki/Backpropagation
[4] How the backpropagation algorithm works. http://neuralnetworksanddeeplearning.com/chap2.html
[5] 神经网络和反向传播算法推导. http://www.mamicode.com/info-detail-671452.html
机器学习公开课笔记(5):神经网络(Neural Network)——学习
标签:
原文地址:http://www.cnblogs.com/python27/p/MachineLearningWeek05.html