标签:
广义上讲,任何在学习过程中应用到矩阵特征值分解的方法均叫做谱学习方法,比如主成分分析(PCA),线性判别成分分析(LDA),流形学习中的谱嵌入方法,谱聚类等等。
由于科苑向世明老师课件上面关于ng的谱聚类算法里面与ng大神的论文中写到的算法中有所出入,导致昨天晚上调了一晚上的算法并没有调出满意的结果,今天在网上找到了ng大神的原始paper阅读一遍,虽然还是有很多不理解的地方,还是有了自己的见解。下面是ng算法的流程。

算法第一步先通过高斯函数计算出每个点与其他点的亲和度,与自己的亲和度为0,对于每一个点保留前k_nearest个最近邻的点的亲和度(即k_nearest个亲和度最大的点),其他的亲和度置为0,这里的k作为算法的参数传入
算法第二步先计算度矩阵D,D矩阵为一个对角矩阵,将亲和度矩阵的每一行元素求和放在度矩阵的相应对角元素上面即可,算出对角矩阵后再构造归一化的拉普拉斯矩阵,由于D是对角矩阵,所以D^(-0.5)可以直接理解为对角元素的倒数开根号,然后得到拉普拉斯矩阵
算法第三步求解拉普拉斯矩阵的特征值和特征向量,并按照特征值大小选取对应最大的K个特征值对应的特征向量(这里的K为将数据点聚成的类的个数),每个特征向量按列排列组成K维空间的n个向量即X属于Rn*k
算法第四步将得到的X矩阵按行归一化长度得到矩阵Yn*k
算法第五步将得到的归一化长度的矩阵数据送入k_means算法进行聚类,得到的类别标签即为原始数据点的类别标签
个人对算法的理解是将原始数据点映射到K维数据空间便于更好的将数据分类出来。
下面是算法实现的matlab代码,python代码等有时间写完再贴上来。
function [after_class_data,class_label,acc] = spectral_clustering(dataSet,class_num,sigma,k_near)
Affinity_mat = creat_D(dataSet,k_near,sigma); %创建亲和度矩阵
laplas = get_norm_laplas(Affinity_mat); %得到归一化的拉普拉斯矩阵
[eig_val,eig_vec] = get_special_vector(laplas,class_num); %得到拉普拉斯矩阵的前K大的特征值对应的特征向量
[label,after_center] = k_means(eig_vec,class_num); %将特征向量送入k_means进行聚类
after_class_data = after_center;
class_label = label;
%{
n11 = size(find(label(1:100)==1),2);
n12 = size(find(label(1:100)==2),2);
n21 = size(find(label(1:100)==1),2);
n22 = size(find(label(1:100)==2),2);
n_1 = max(n11,n12);
n_2 = max(n21,n22);
acc = (n_1 + n_2)/size(label,2); %计算分类正确率
%}
%计算亲和度矩阵,用K近邻求取,其余的赋值为0,每个点与本身的亲和度为0
function Affinity_mat = creat_D(dataSet,k,sigma)
[row,col] = size(dataSet);
dis_mat = zeros(row,row);
index_all = zeros(row,row);
%index_all = [];
for i = 1:row
for j=1:row
if i ~= j
dis_mat(i,j) = exp((-sum((dataSet(i,:)-dataSet(j,:)).^2))/(2*sigma.^2));
end
end
end
Affinity = dis_mat;
for t =1:row
[sort_dis,index] = sort(Affinity(t,:),‘descend‘);
index_all(t,:) = index;
end
for ii = 1:row
temp_index = index_all(ii,:);
temp_clear = temp_index(k+1:row);
%temp_one = temp_index(1:k);
Affinity(ii,temp_clear) = 0;
%Affinity(ii,temp_one) = 1;
Affinity(ii,ii) = 0;
end
Affinity_mat = Affinity;
function laplas = get_norm_laplas(Affinity_mat)
row = size(Affinity_mat,1);
du = zeros(row,row);
%col_sum = sum(Affinity_mat);
for i=1:row
du(i,i) = sum(Affinity_mat(i,:)); %求度矩阵
end
dn = du^(-0.5);
laplas = dn*Affinity_mat*dn; %归一化的laplas
%求k个最小的特征值和对应的特征向量
function [eig_val,special_vector] = get_special_vector(laplas,k)
eig_con = eig(laplas);
[vector,x] = eig(laplas);
[sort_vec,index] = sort(eig_con,‘descend‘);
eig_val = eig_con(index(1:k));
temp_vector = vector(:,index(1:k));
[row,col] = size(temp_vector);
y = zeros(row,col);
for i=1:row
s = (sum(temp_vector(i,:).^2)).^(0.5); %特征向量的归一化
for j=1:col
y(i,j) = temp_vector(i,j)/s;
end
end
special_vector = y;
k_means聚类算法代码如下:
function [class_type,after_center] = k_means(dataSet,class_number)
[data_row,data_col] = size(dataSet);
%last_label = zeros(1,data_row);
label = ones(1,data_row);
ini_center = randn(class_number,data_col)
%ini_center = [1.1437 0.9726;-0.5316 -0.5223];
new_center = zeros(class_number,data_col);
while (sum(sum(abs(ini_center - new_center) > 1e-5)) > 0)
new_center = ini_center;
for i=1:data_row
min_dis = Inf;
belong_class = 1; %用该变量来存储属于的类别,如为1,则归属为第一类。。。
for j=1:class_number
cur_dis = sum((ini_center(j,:)-dataSet(i,:)).^2);
if cur_dis < min_dis
min_dis = cur_dis;
belong_class = j;
end
end
label(i) = belong_class;
end %找到每一个类的归属标签
%重新计算归属类的中心点
for k=1:class_number
class_index = find(label==k);
n = size(class_index,2);
%{
sum_x = sum(dataSet(class_index,1)); %算出类别k中的x的和
sum_y = sum(dataSet(class_index,2));
ini_center(k,1) = sum_x/n;
ini_center(k,2) = sum_y/n; %更新归属类的中心
%}
ini_center(k,:) = sum(dataSet(class_index,:))./n;
end
end
class_type = label;
after_center = new_center;
用月牙型数据进行测试分类情况,设定sigma参数为35,当取k_nearest=10,20,30时,对应的分类图如下
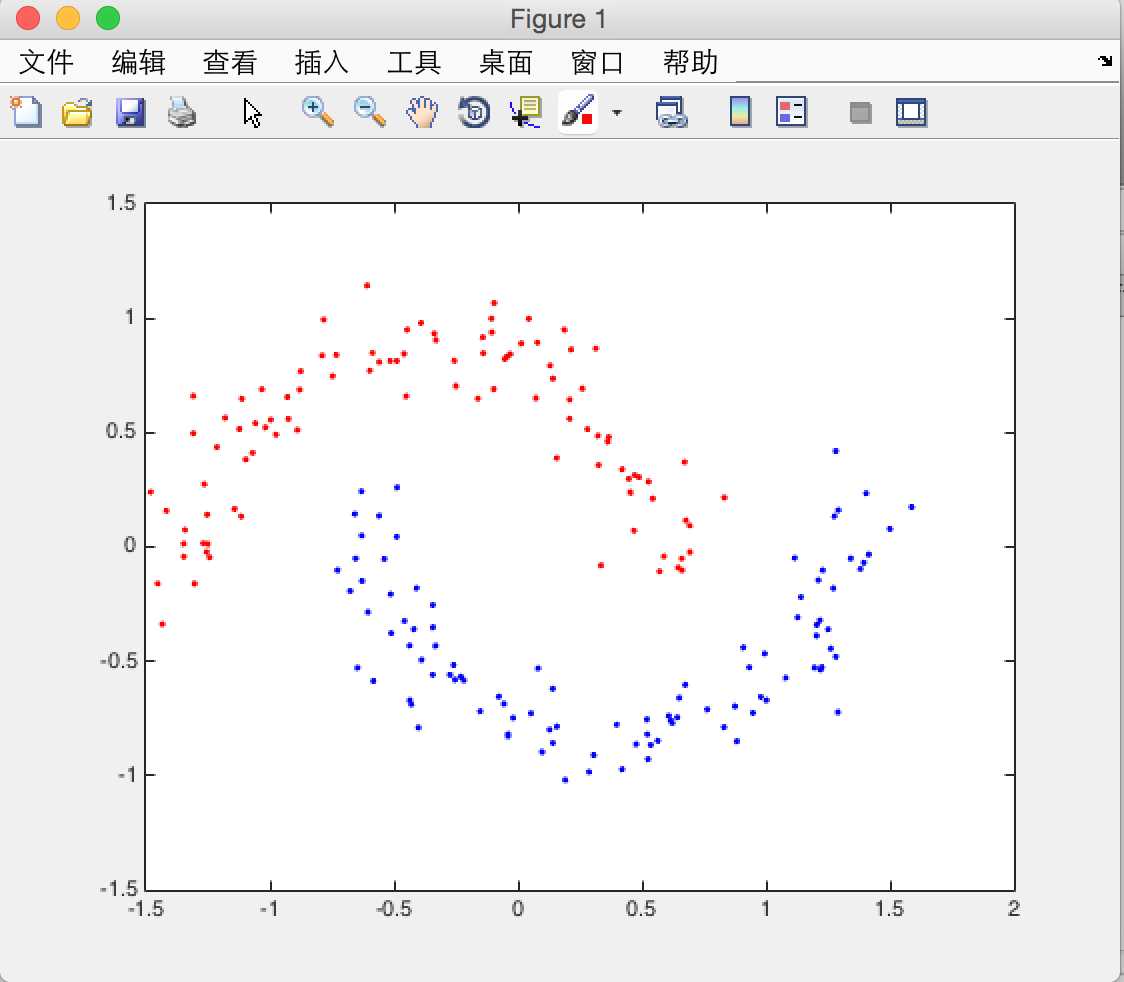
k_nearest = 10
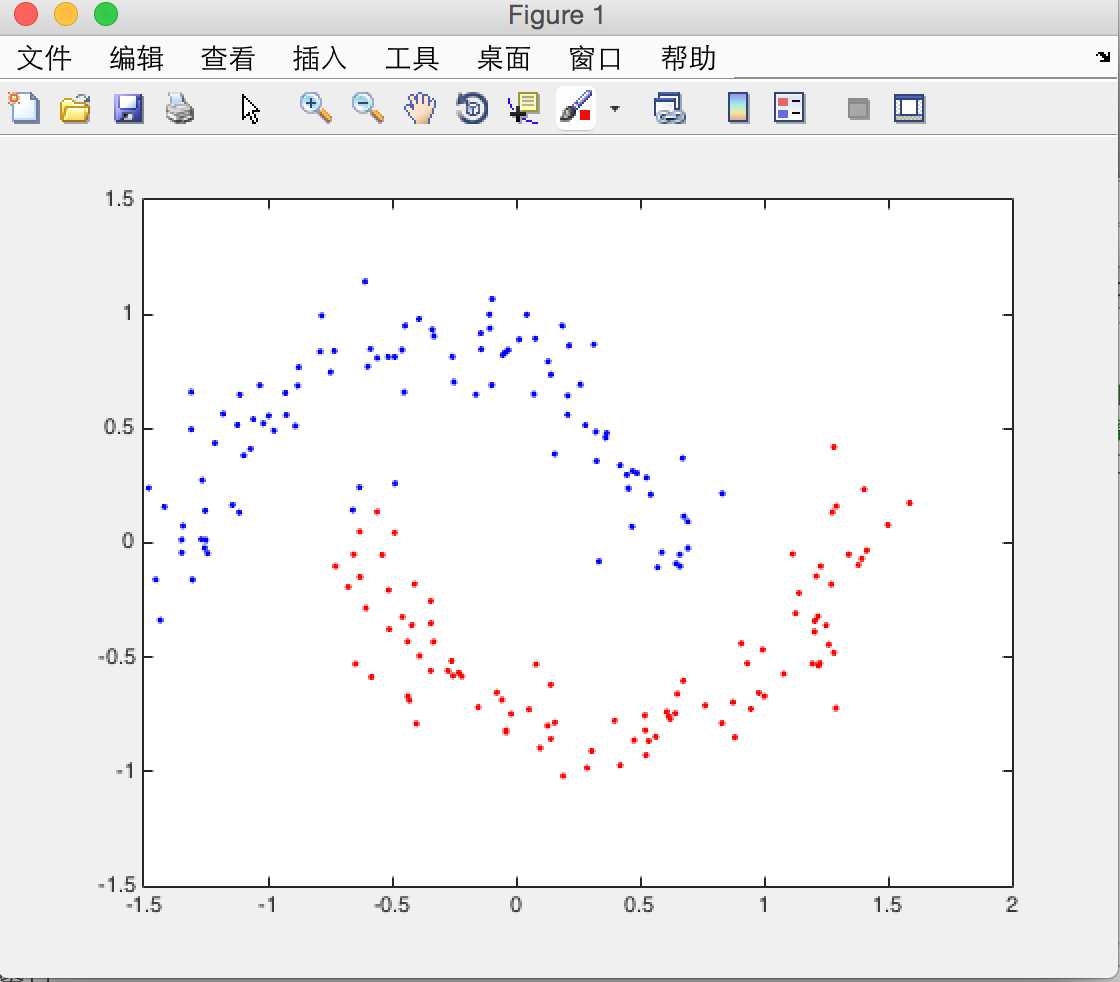
k_nearest = 20
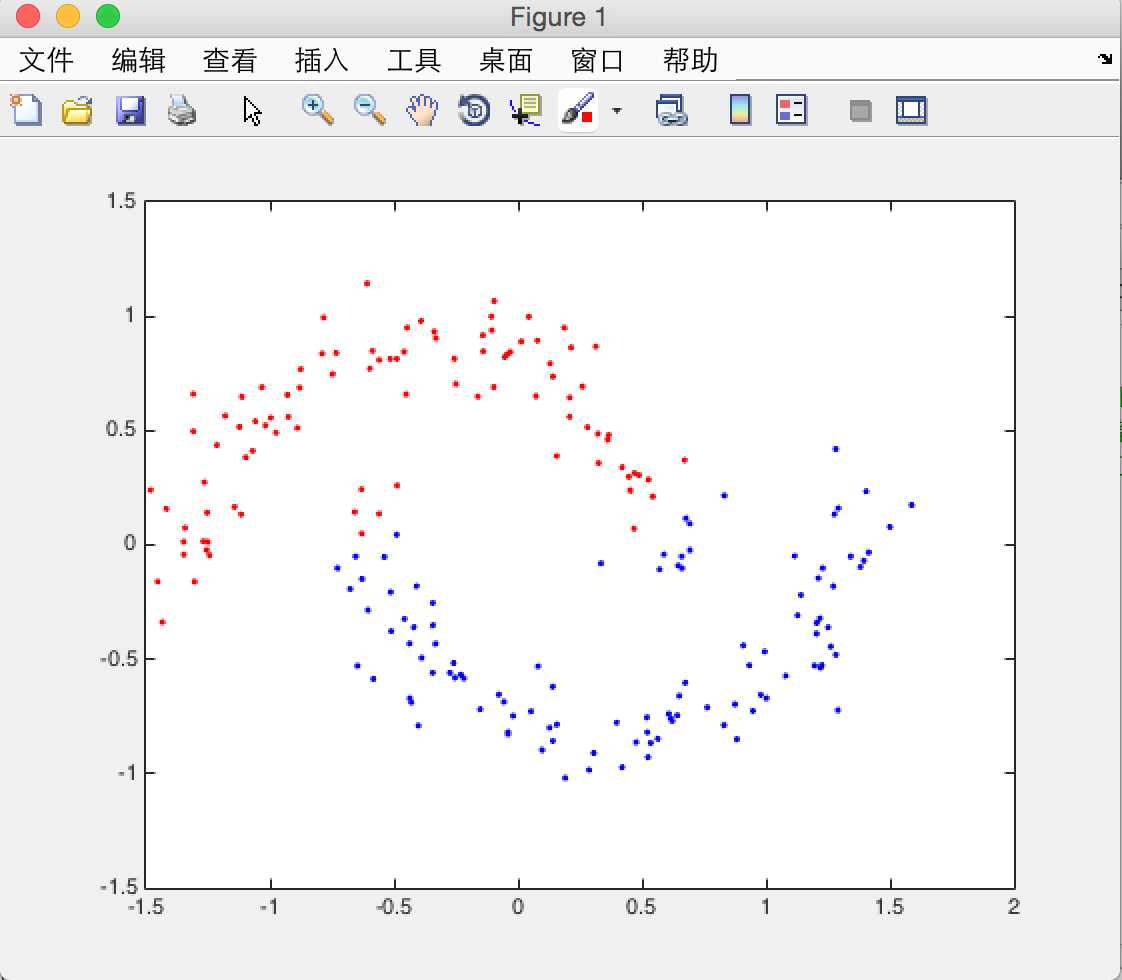
k_nearest = 30
随着最近邻参数k_nearest的增大,分类的正确逐渐下降。由于此k_means算法的初始点使用randn生成,而初始点的选取对结果是有影响的,故在跑程序途中会出现结果不理想出现Nan的情况,这些比较正常,多试几次就能得到比较稳定的分类结果了。以后会逐渐的用python来实现算法,后续会上传python代码。
感慨:特征值分解,特征向量映射原始点到K维空间,大神们是怎么想到了呢,太神奇了,个人的数学思维和素养需要进一步提升,虽然算法里面的一些数学原理上的东西还不是很理解,但是我会加油的。
标签:
原文地址:http://www.cnblogs.com/eric-D123/p/eric_d.html