标签:
论文题目:Data-driven soft sensor development based on deep learning technique
摘要:利用深度学习来建立常减压装置的软测量回归模型,对以后的课题学习有用,主要本人是化工集成和数据挖掘方向的,所以这篇文章还是对我比较有吸引力的,至于文章难度如何我就不置臧否。
1---深度神经网络结构的理解
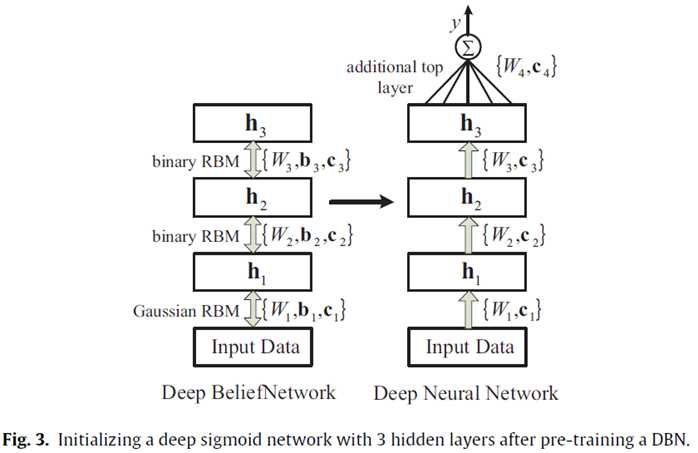
以前最普通的反向传播(back-propagation)训练的神经网络基本上都是随机生成一组初始参数然后再用梯度下降法来调正参数,从而达到一个较好的拟合效果。一般用的神经网络最多的就是3层结构,输入层、单隐层和一个输出层,这种结构的神经网络据柯尔莫哥洛夫定理证明是可以逼近任意连续函数到任意精度,所以一般来说3层结构的也够了。但这种方法的缺点是梯度最后会变得很小,学习过程很慢,会优化到一个局部极小值。深度学习(deep learning)则是采用多层隐含层来训练,而且采用的训练方法也是半监督(semi-supervised)的训练算法。深度学习技术的训练过程主要包括两个阶段(就是在这解释啥叫半监督),无监督的预训练阶段和监督模式的反向传播训练。在无监督的预训练阶段,首先建立的是一个深度信任网络(deep belief network, DBN),并对其进行预训练,预训练得到的结果作为下一步的监督的反向传播训练初始参数。接下来便是对已经预训练的网络进行反向传播训练。这里的DBN的构建就要提到一个叫restricted Boltzmann machines (RBMs)的东西了,反正这玩意儿也是机器学习里面的一个模型,好像是叫什么Boltzmann机的。那么这里的DBN的层次结构的构建就是好几个这个RBMs堆起来的。如下图所示:(请原作者原谅我盗图)
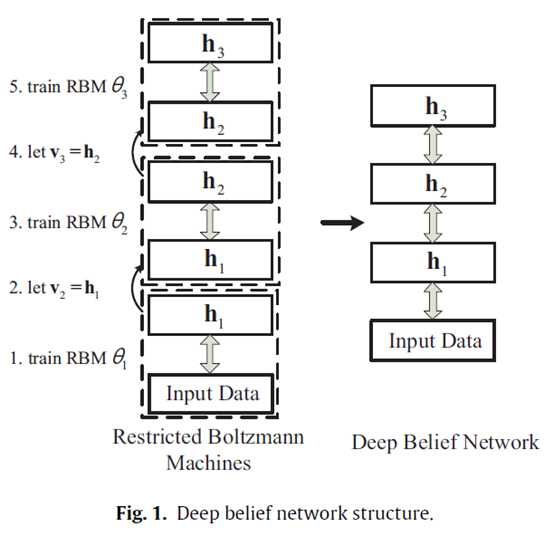
我所理解的就是每个虚线框都是一个RBMs,然后下面一个RBMs的输出就是作为上面的RBMs的输入,管他对不对先这样理解吧。InputData和h1就构成了最下面的一个RBMs,所以下面来就是一个一个的训练RBMs吧,就是所谓的预训练了吧。那么这个DBN的训练就是一个逐层训练的方案(greedy layer-wise scheme),从最下面一层一直到最上一层。RBM theta1最先训练,然后是RBM theta2,……,依次类推,那么在这个训练过程中的特征是逐层抽取的,并逐层向上传播的,训练的目标或者是方向是使每个RBM的P(vl)达到最大,就是一个使该RBM的输入向量v作为自变量的某个函数值最大的方向。(我觉得)在预训练的过程中,每个RBM都是只对自己的这一层负责,而不牵涉到其他层的参数的改变。总结的来说就是,预训练的过程完全是无监督的训练过程。
2---DBN的预训练过程
在谈到具体的RBMs训练,就要到了具体的数学上的细节了。
RBM的基础
最开始要介绍的是基本的基于能量的RBM模型(basic energy-based model),这里其实就是给每个输入向量一个标量值,在后面是作为一个优化指标的,在这里就喊他能量(energy)。那么这个函数的定义是:
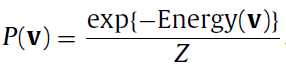
其中Z是:
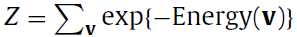
也就是每个输入向量所得到的值(就是exp()所算出来的)的和,那么P(v)就是对应向量v所占的比,给这个过程一个名字就是归一化(normalization),Z就是这个normalizing factor。那么到这来了就只有Energy(v)这个函数不明了,那么这个Energy(v)究竟是啥呢?
基于能量的模型有不同的能量函数,在RBM中的能量函数是一个二阶的多项式(a second-order polynomial),如果中文没有翻译错的话。
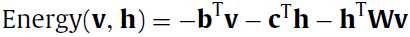
我擦,明明之前Energy这个函数的参数只有一个向量v,这咋又多了一个h捏?不急,论文中又说了,这个v和h都是二进制值(0和1)组成的向量,
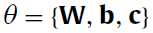
theta呢是能量函数的参数集,即W,b,c都是我们要训练的参数的。
上面所讲的能量函数模型是二进制的RBMs(binary RBMs),据论文中说在实际中用的最多的,但是想想v是二进制的,这样的话变量只能是离散的,那么直接拿来做连续变量的回归肯定是大大的不行,这里呢,为了处理连续的输入变量,将二进制的RBMs扩展为Gaussian RBMs:
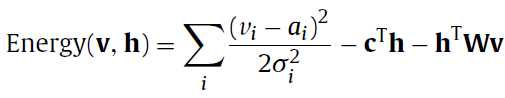
看看有啥变化,多了
 ,
, 和
和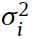 ,
,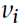 呢是原来的输入向量v的第i个分量这是没啥问题的,
呢是原来的输入向量v的第i个分量这是没啥问题的,
然后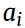 和
和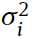 是高斯分布的平均和标准偏差(mean and standard deviation of the Gaussian distribution),对i来说。这里呢v从原来的二进制变为连续变量了,但是这里的h仍然是二进制变量。
是高斯分布的平均和标准偏差(mean and standard deviation of the Gaussian distribution),对i来说。这里呢v从原来的二进制变为连续变量了,但是这里的h仍然是二进制变量。
如果是到这而的话,我们的要训练的参数有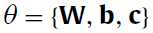 ,
,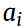 和
和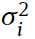 。在实际中输入数据都会归一化到(0,1),高斯分布(也就是标准的正态分布好像是这样的参数),那么Gaussian RBMs就会被化简为normalized Gaussian RBMs:
。在实际中输入数据都会归一化到(0,1),高斯分布(也就是标准的正态分布好像是这样的参数),那么Gaussian RBMs就会被化简为normalized Gaussian RBMs:
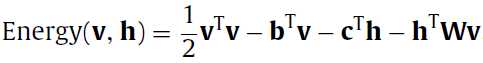
(注记:到这儿的话我觉得没有normalized的Gaussian RBMs那个公式:
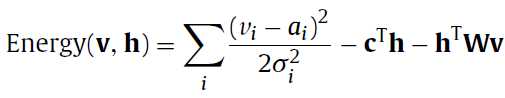
好像少了一项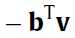 ,应该是的)
,应该是的)
到这的话,Energy函数就确定了要用normalized Gaussian RBMs了。
?
现在我们知道的就是输入v了,因为你肯定的有输入的样本来训练嘛,如果没有请自行生成。那么我们要通过v来预估h了。预估的方向(也就是计算的方向)就是:
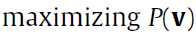
即最大后面的那个P了。
这里还是用到的是gradient descent(梯度下降算法了,简单又实用),但是求导过程真的不堪入目有木有,每次求导都让你想屎。呵呵,如下面的公式:

至于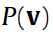 前面的那个求对数的
前面的那个求对数的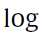 是求极值的时候的一种处理手段,我觉得不必深究了。
是求极值的时候的一种处理手段,我觉得不必深究了。
面对这么一大串公式我们应怎样解毒呢?
论文里又突然冒出个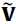 ,这真是让我不知所措。
,这真是让我不知所措。
在这儿,光看该文然后自己推到仍然推不倒,只怪我太搓……然后又参考了如下文献:
http://machinelearning.wustl.edu/mlpapers/paper_files/NIPS2006_739.pdf
Bengio Y, Lamblin P, Popovici D, et al. Greedy layer-wise training of deep networks[J]. Advances in neural information processing systems, 2007, 19: 153.
?
下面这步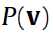 变成
变成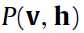 ,多了一个求和指标集
,多了一个求和指标集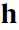 ,由前面我们知道这个
,由前面我们知道这个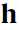 是一个二进制的向量。这一步变过来应该没有啥问题。
是一个二进制的向量。这一步变过来应该没有啥问题。
?
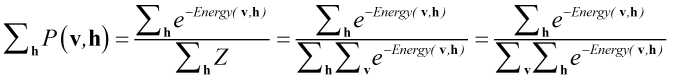
?
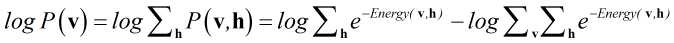
?
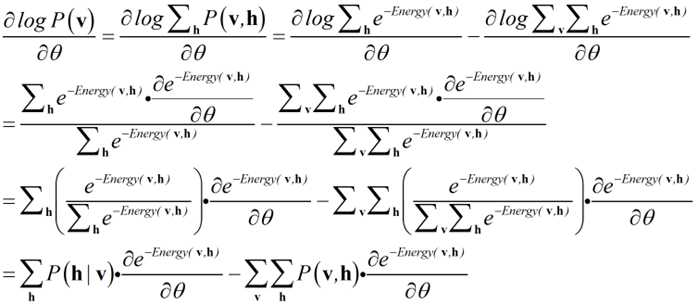
?
到这里来了终于感受到高等数学求导的用处了,虽然不是数学分析,又要被嘲讽了。反正直接看原文我是不知道咋推的,参考了其他的资料之后终于可以推出论文中的公式。其实这公式看着一大串,一点技术含量都没有的……
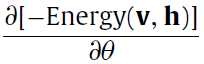 和
和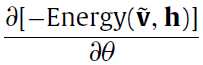 的计算是很简单的,我也这么觉得,因为前面也说过能量函数
的计算是很简单的,我也这么觉得,因为前面也说过能量函数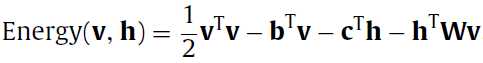 是一个二阶的多项式,多项式的求导还能复杂到哪儿去(希望不要被打脸)。
是一个二阶的多项式,多项式的求导还能复杂到哪儿去(希望不要被打脸)。
?
?
3---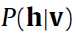 的计算过程
的计算过程
那么接下来的关键之处就是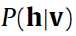 和
和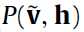 了。这个呢,大牛们也找出了如何算的方法。如果对概论的一点知识还有印象的话,
了。这个呢,大牛们也找出了如何算的方法。如果对概论的一点知识还有印象的话,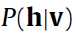 是一个条件概率,反正我是快忘了,这里的意思目测是给定了
是一个条件概率,反正我是快忘了,这里的意思目测是给定了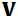 之后,算出在条件
之后,算出在条件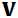 下的,
下的,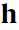 的概率。
的概率。
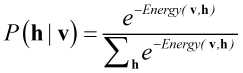
对于二进制的RBM,条件概率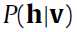 和条件概率
和条件概率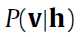 计算公式如下:
计算公式如下:
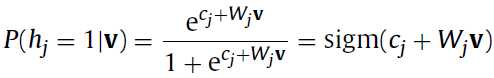
?
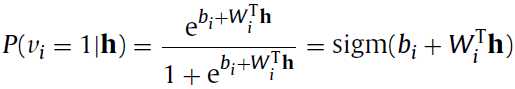
?
我觉得这个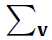 和
和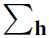 在
在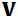 和
和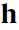 都是二进制的时候,是不是就是把其中一个分量设为1,然后其他的都设为0这样子轮询的来算。
都是二进制的时候,是不是就是把其中一个分量设为1,然后其他的都设为0这样子轮询的来算。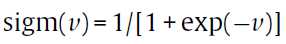 是在机器学习里面很常见的一个函数。
是在机器学习里面很常见的一个函数。
而如果对于Gaussian RBM来说呢,则变成下面的两个式子:
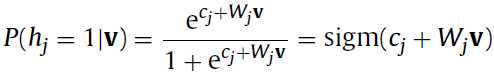
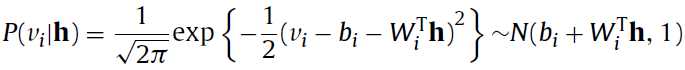
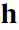 仍然是二进制,而
仍然是二进制,而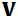 已经变为连续变量了,而且第二个公式也给出了
已经变为连续变量了,而且第二个公式也给出了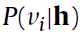 是符合以
是符合以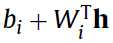 为中心的正态分布(normal distribution)。到这儿
为中心的正态分布(normal distribution)。到这儿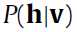 已经可以算了。
已经可以算了。
?
4----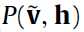 的计算过程:
的计算过程:
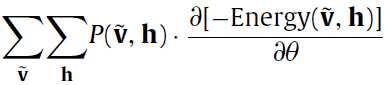
二阶段吉布斯采样?(two-stage Gibbs Sampler),是一个高效的逼近采样的方法(到这里出来了一个新东西,不太懂)。通过迭代下面的式子构建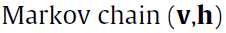 (马尔科夫链):
(马尔科夫链):
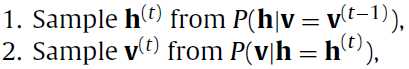
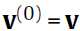 是初始的,我觉得这里的意思就是
是初始的,我觉得这里的意思就是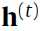 和
和 都是彼此轮着算。就这样一直算下去可以收敛,得到最终的真正的联合分布(true joint distribution)
都是彼此轮着算。就这样一直算下去可以收敛,得到最终的真正的联合分布(true joint distribution)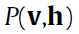 。
。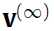 和
和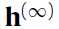 都像是从
都像是从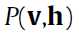 的理想采样。这样一直算下去的缺点就是你要一直计算梯度,可见这样算下去很花时间。这里的方法就是用
的理想采样。这样一直算下去的缺点就是你要一直计算梯度,可见这样算下去很花时间。这里的方法就是用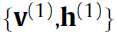 来代替
来代替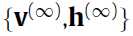 ,作一个二阶的逼近,这就是所谓的contrastive divergence algorithm吧。
,作一个二阶的逼近,这就是所谓的contrastive divergence algorithm吧。

?
5--- 的计算过程以及更新参数
的计算过程以及更新参数
对于二进制的RBM和高斯RBM都有如下的计算公式,这个求下导基本上也出来了:
求导求完了之后就可计算新旧变量之间的差值,来更新参数了
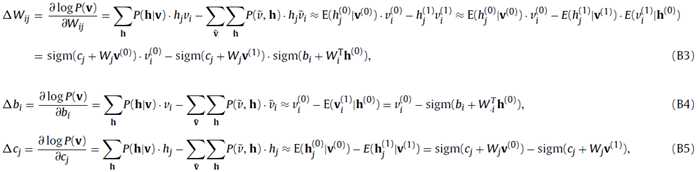
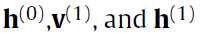 是通过一步马尔科夫链计算出来的,公式里面出现了
是通过一步马尔科夫链计算出来的,公式里面出现了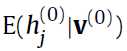 是利用了条件期望代替马尔科夫链计算出来的binary states,避免出现计算波动(反正这个是原文中所说的)。
是利用了条件期望代替马尔科夫链计算出来的binary states,避免出现计算波动(反正这个是原文中所说的)。
?
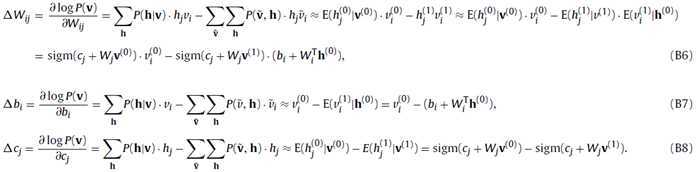
?
然后根据公式的正项和负项来分别计算,下层的RBMs是较低级的特征,而上面的RBMs是高级的特征,包含input-vector的那层是用的Gaussian RBMs而上面的都是binary RBMs。当无监督的DBN的训练结束之后,就开始了有监督的训练。前面的待优化的参数如:
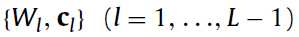 都的初始值都已经有了,然后最后一层的
都的初始值都已经有了,然后最后一层的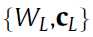 需要随机生成,即最后一个隐含层到输出层之间的参数在无监督的预训练过程中是没有的。然后多层神经网络的参数都有了之后就可以用back-propagation来调节了。
需要随机生成,即最后一个隐含层到输出层之间的参数在无监督的预训练过程中是没有的。然后多层神经网络的参数都有了之后就可以用back-propagation来调节了。
?
?
利用deep neural network来建立所需要模型的步骤可以总结如下:
step 1:首先需要对数据要归一化处理,样本处理的目标是zero mean和unit variance
step 2:确定DNN的结构,然后以无监督的方式预训练DBN每一层的RBM
step 3:用预训练的DBN的结果作为deep neural network的初始参数
step 4:用back-propagation的方法来调节参数
step 5:用另外的数据集来验证所建立的deep network,如果存在过拟合那么需要返回step 4
step 6:用测试数据来测试所建立的模型是否正确,如果不满意则返回step 2
标签:
原文地址:http://www.cnblogs.com/tuhooo/p/5112759.html