查找算法：二分查找、顺序查找

时间：2016-01-09 15:14:17 阅读：190 评论：0 收藏：0 [点我收藏+]

标签：

08年9月入学，12年7月毕业，结束了我在软件学院愉快丰富的大学生活。此系列是对四年专业课程学习的回顾，索引参见：http://blog.csdn.net/xiaowei_cqu/article/details/7747205

查找算法

查找算法是在存在的序列（list）中查找特定的目标（target），要求序列中每个记录必须与一个关键词（key）关联才能进行查找。

查找算法通常需要两个输入：

1、被查找的序列

2、要查找的关键词

查找算法的输出参数和返回值：

1、返回类型为 Error_code 的值用以表示是否查找成功

2、如果查找成功，返回 success，输出参数 position 定位到目标所在位置

3、如果查找失败，返回 not present，输出参数可能是未定义或不同于已有位置的任何值

顺序查找算法

顺序查找算法的思路很简单：从表的第一个元素开始一个一个向下查找，如果有和目标一致的元素，查找成功；如果到最后一个元素仍没有目标元素，则查找失败。

【实验说明】

题目：编写一个程序，对顺序表{3,6,2,10,1,8,5,7,4,9},采用顺序查找关键字5的过程。要求输出：
1）原顺序表；2）查找到关键字的位置；3）进行比较的次数。
1.首先要编写类表List。需要满足最基本的操作插入insert（），获取retrieve（），以及得到大小size（）。
2.我们观察题目要求，表中虽然存储的是简单的整数，但如果我们使用List<int>对象显然无法记录比较次数，所以我们自己写一个类Key通过其内部int类型的数据成员来记录存于表中的值，并模仿int基本的逻辑操作，即编写重载逻辑运算符，同时增加一个静态数据成员comparisons用于记录其比较操作的次数。
3.准备工作做好之后开始编写顺序查找算法。算法的思路很简单，也较易实现，从表中第一个元素开始比较，发现目标则返回元素所在表中位置；若遍历之后没有目标，则查找失败，返回-1表示表中没有目标元素。

4.按题目要求编写最后的输出函数。

【相关代码】

函数 sequential_search

[cpp] view plain copy

int sequential_search(const List<int> &the_list,
const Key &target)
/*Post: If an entry in the_list is equal to target, then return the position
of this entry.
Otherwise return -1
*/
{
int position;
int s=the_list.size();
for(position=0;position<s;position++){
int data;
the_list.retrieve(position,data);
if(data==target){
return position;
}
}
return -1;
}

二分查找算法

二分查找前提是表是按递增或递减顺序的规范表。此次实验中我们使用的是递增表。
二分查找从表中间开始查找目标元素。如果找到一致元素，则查找成功。如果中间元素比目标元素小，则仍用二分查找方法查找表的后半部分（表是递增排列的），反之中间元素比目标元素大，则查找表的前半部分。

【实验说明】

题目：编写一个程序，对有序表{1,2,3,4,5,6,7,8,9,10},采用二分查找关键字9的过程。要求输出：
1）原顺序表；2）查找到关键字的位置；3）进行比较的次数。
1.二分查找算法的前提是表必须是有序的，如题目中是递增方式排列的表。实现表的有序一方面是用户规范输入，另一方面我们也可以编写有序的类来方便用户的输入。
所以从List中派生类Oredered_list，重新编写函数Error_code insert（int position，const Record &data），使插入的位置不满足表的有序条件时，不能插入。
同时编写插入的重载函数 Error_code insert(const Record &data)，可以直接插入到合适的位置，方便用户输入。
2.仍使用题目1中的Key来表示目标
3.实现二分查找算法。通过书中的学习，我们直接使用添加相等判断的二分查找算法。即每次从表的中间元素开始比较，如果得到目标则返回元素所在表中位置；如果中间元素小于目标元素，则对右半部分继续二分查找；反之对前半部分表进行二分查找。若最后都没有目标元素，返回-1用以表示表中没有目标元素。

4.仍使用题目1编写的输出函数将结果输出。
/*注意这里因为Ordered_list是从List中派生而来，所以虽然print_out函数中第一个参数类型是List<int>，仍可以使用，而不用编写重载函数*/

【相关代码】

函数 binary_search

[cpp] view plain copy

int binary_search(const Ordered_list<int> &the_list,
const Key &target)
/*Post: If an entry in the_list is equal to target, then return the position
of this entry.
Otherwise return -1
*/
{
int position;
int data;
int bottom=0,top=the_list.size()-1;
while(bottom<=top){
position=(bottom+top)>>1;
the_list.retrieve(position,data);
if(data==target)
return position;
if(data<target)bottom=position+1;
else top=position-1;
}
return -1;
}

【过程记录】

实验截图：

【结果分析】

A.实现顺序查找算法

1.顺序查找算法思路很简单，就是一种遍历的思想，一个个查找目标元素，实现也很简单。
2.对于有n个元素的表适用顺序查找。比较次数：不成功：比较n次。成功查找：最好的情况为1次，即第一个元素即为目标元素；最差的情况为n次；平均比较次数（n+1）/2次。
所以当表很大时，顺序查找的代价是很大的。
3.顺序查找算法不会有重复的比较出现，即一旦找到即成功，但同时这种代价是当表中有重复的目标元素时（比如有多个目标元素）我们只能得到第一个元素的位置。

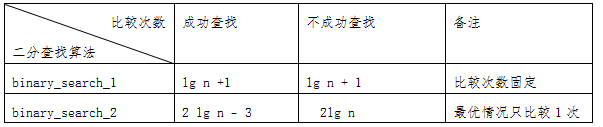
B.实现二分查找算法

1.二分查找法思路：递增排列的表，首先从中间元素开始查找，如果元素比目标元素小，则查找后半部分表，反之查找前半部分表，并重复这一过程。这样每次查找中我们都把表的长度减半。
2.二分查找在实现中有量bottom和top，每次减半的过程体现在bottom和top的改变上，在代码的实现上可以使用单纯的循环或者用函数递归的思想。
递归思想更容易理解，但编写之后我们发现函数是尾递归，尾递归通常可以用简单的循环实现，循环在操作来说没有了函数调用的过程，更节省时间和空间。
3.编码中小小地方的改动可能对程序有很大的改观。

如上述两种二分查找binary_search_1（不比较等于的情况）binary_search_2（添加等于情况）

实验代码下载：http://download.csdn.net/detail/xiaowei_cqu/4437702

（转载请注明作者和出处：http://blog.csdn.net/xiaowei_cqu 未经允许请勿用于商业用途）

查找算法：二分查找、顺序查找

标签：

原文地址：http://www.cnblogs.com/GarfieldEr007/p/5116339.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行