标签：
算法描述：
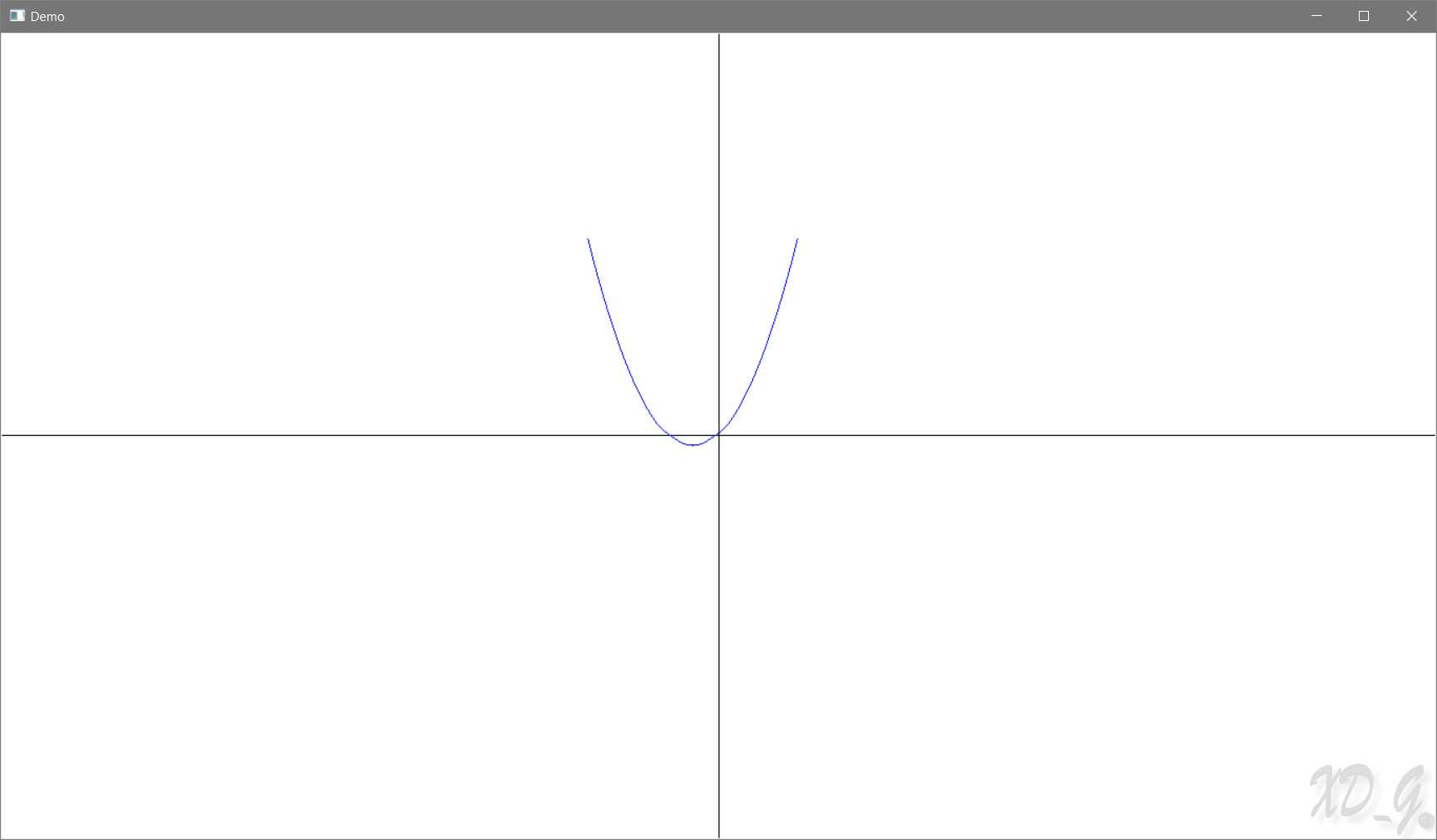
对于抛物线，先分析一种最为特殊的情况，就是对称轴为y轴，且经过坐标原点。如图所示：
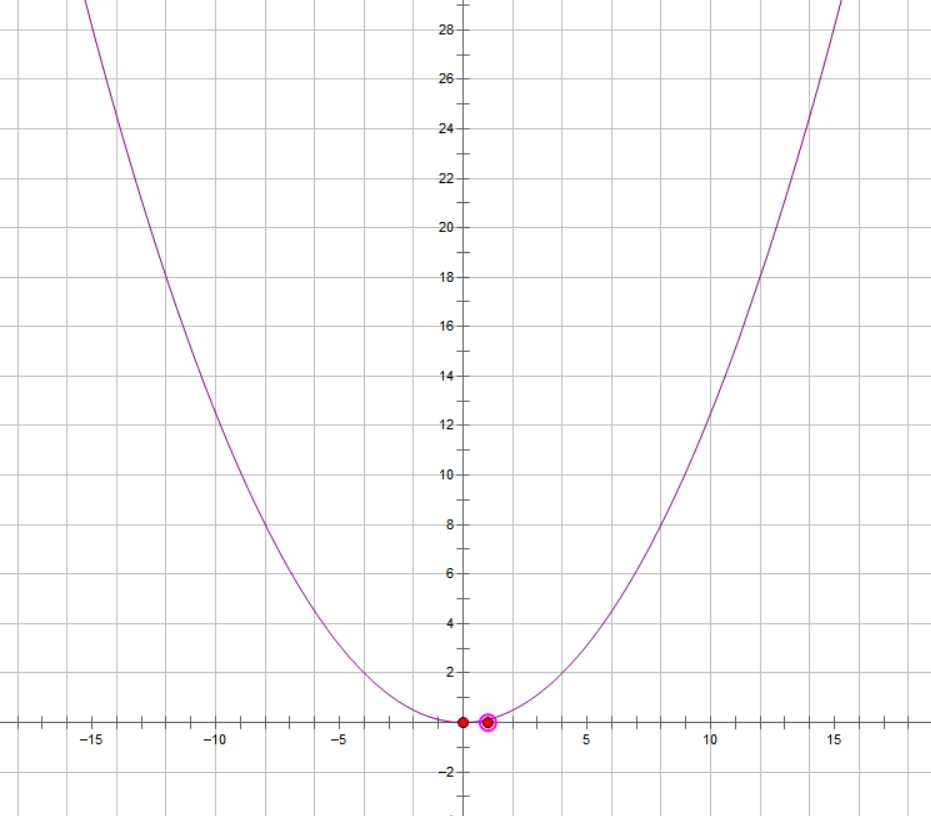
只要生成了这样一个抛物线，那么一般情况下的抛物线都可以凭借这种特殊情况进行平移、旋转得到。而由于该特殊情况下的抛物线在y轴两侧是对称的，所以只需要解决第一象限内的抛物线的生成就能够得到完整的图像。
那么如何得到这种特殊情况下的抛物线
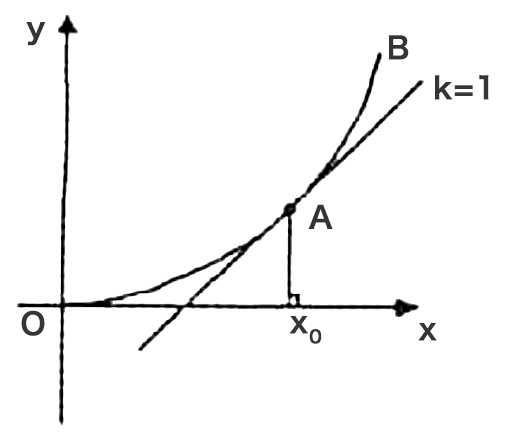
由上图可知，假设一点在抛物线第一象限上从原点开始移动，并过该点A作抛物线的切线，那么根据切线的斜率k=1可以将该象限内的抛物线分为两个部分，一部分为点A左边，切线斜率全部小于1；另外一部分为点A右边，切线斜率全部大于1。
根据之前中点生成算法的思想可知，在左半部分，每次生成可将X坐标递增1，根据决策参数判断Y坐标是否增加
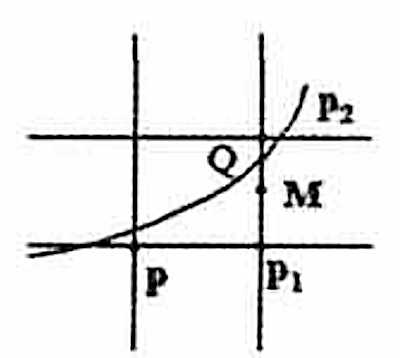区域1
在右半部分，每次生成可将Y坐标递增1，根据决策参数判断X坐标是否增加。
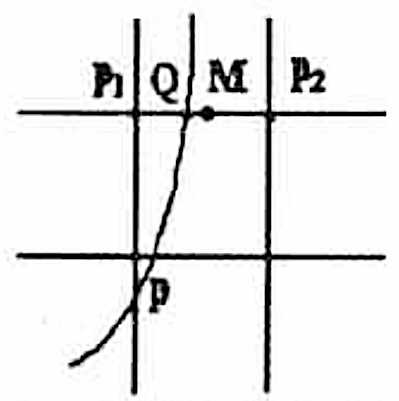
区域2
接下来就是决策参数的推导：
抛物线方程为
，则该曲线方程有两种形式：
区域1：
当
时：下一个点的坐标应该选择
,此时:
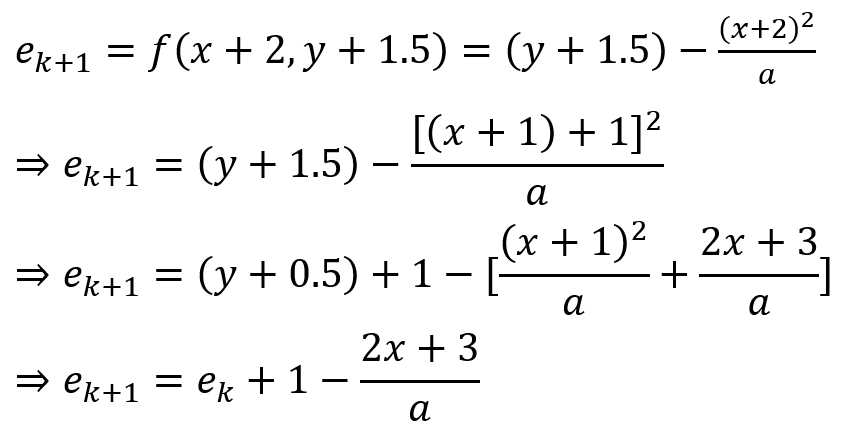
当
时：下一个点的坐标应该选择
,此时:
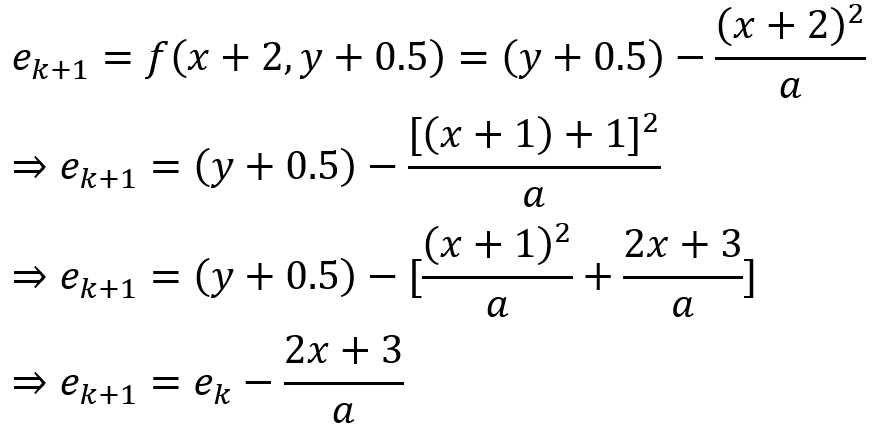
区域2：
当时：下一个点的坐标应该选择
,此时:
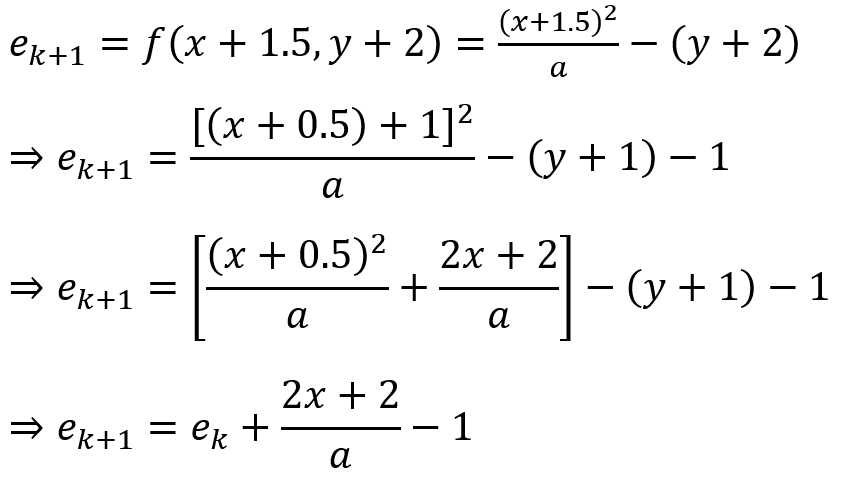
当时：下一个点的坐标应该选择
,此时:
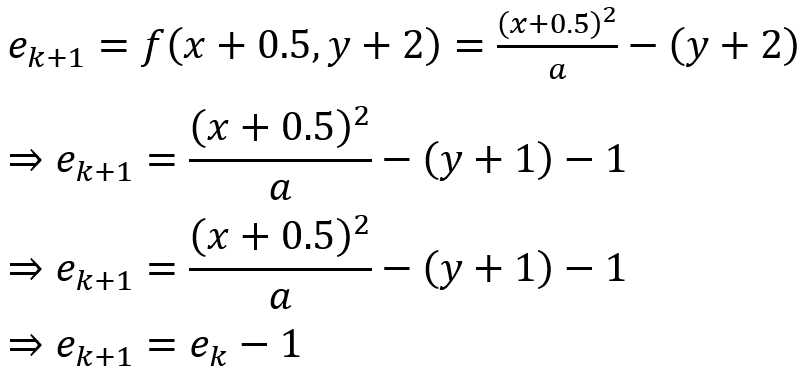
详细代码：Computer Graphics - code_1
生成结果：
标签：
原文地址：http://www.cnblogs.com/xd-g/p/5118522.html
