标签：
算法描述：
Liang_Barsky算法的基本出发点是直线的参数方程。给出任意一条直线段，两端点分别为
和
，令
，
则直线的参数方程为：
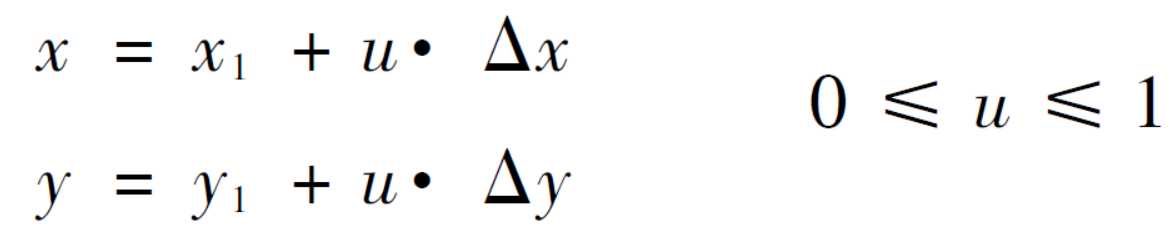
如果直线上任意一点位于窗口内，则必须满足下列关系式：
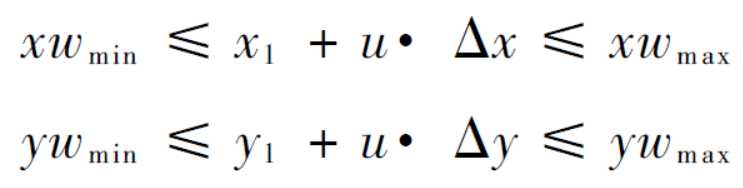
上述不等式可以表示为：
其中p和q定义为：
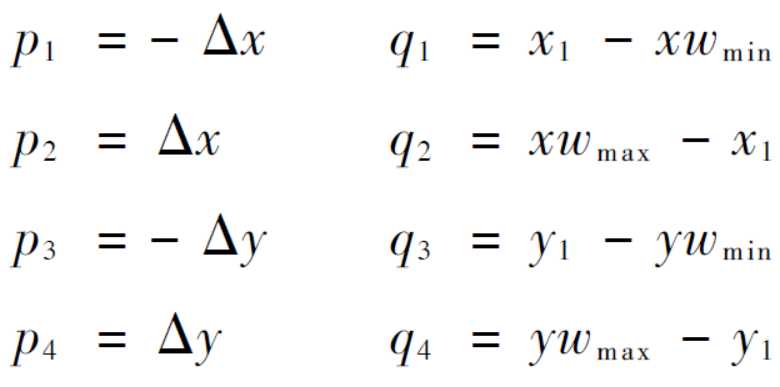
任何一条直线如果平行于某一条裁剪边界，则有
，下标k 对应于直线段平行的窗口边界（
,并且分别表示裁剪窗口的左、右、下、上边界）。如果对于某一个k值，满足
，那么直线完全在窗口的外面，可以抛弃。如果
，则该直线在它所平行的窗口边界的内部，还需要进一步计算才能确定直线是否在窗口内、外或相交。当
时，表示直线是从裁剪边界的外部延伸到内部，如果
，则表示直线是从裁剪边界的内部延伸到外部的。对于pk≠０，可以利用式 计算出直线与边界k的交点的参数u。
对于每一条直线，可以计算出直线位于裁剪窗口内线段的参数值
、
。的值是由那些使得直线是从外部延伸到内部的窗口边界决定。
对于这些边，计算
。值取
以及０构成的集合中的最大值。
的值是由那些使得直线是从内部延伸到外部的窗口边界决定的。
计算出，取和１构成的集合中的最小值。如果＞，这条直线完全在窗口的外面，可以简单抛弃，否则根据参数u的两个值，计算出裁剪后线段的端点。
详细代码：Computer Graphics - code_1
生成结果：
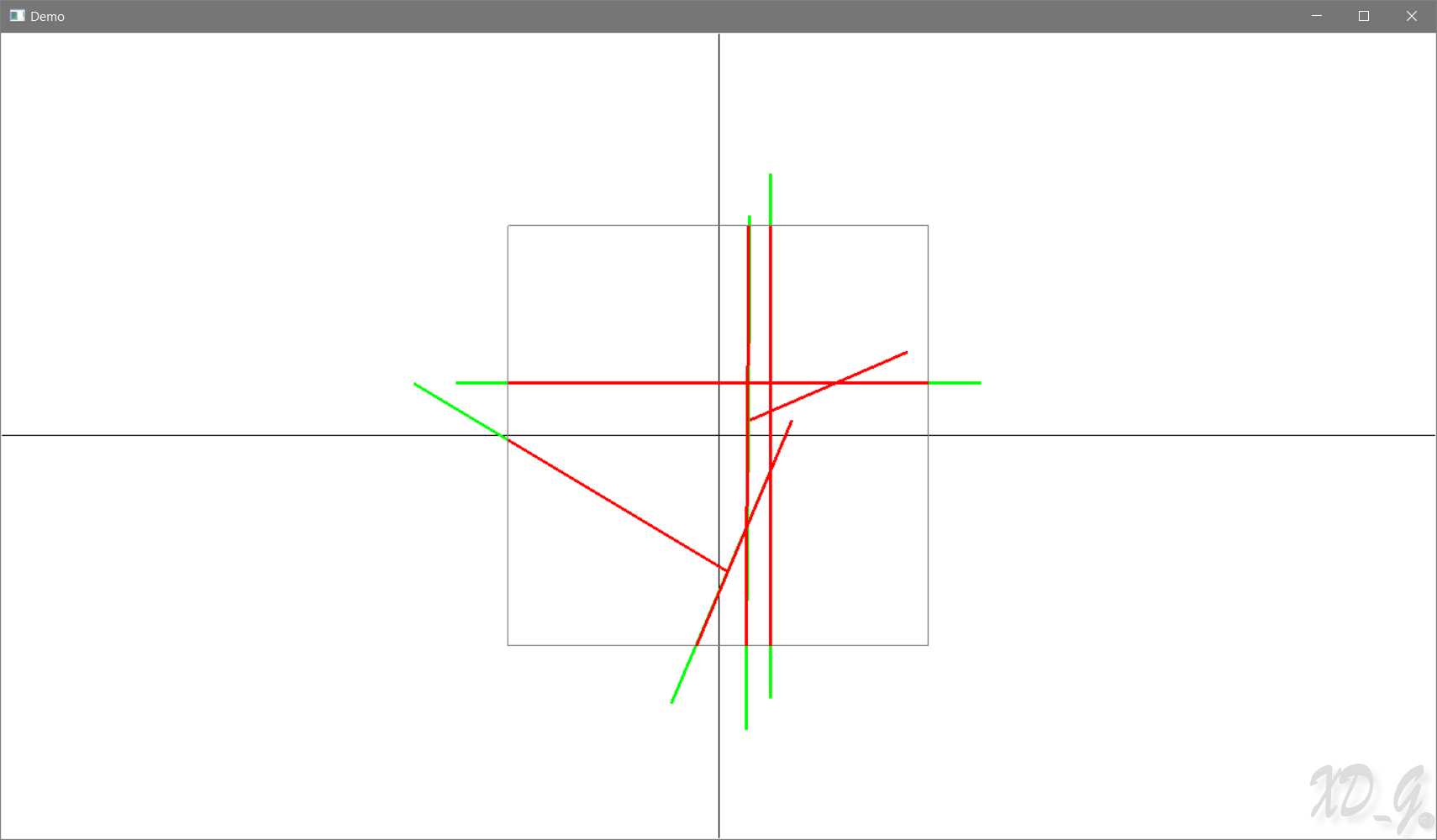
计算机图形学 - 线段裁剪 - Liang Barsky算法（梁友栋算法）
标签：
原文地址：http://www.cnblogs.com/xd-g/p/5118764.html
