分治算法（一）

时间：2016-02-05 01:38:48 阅读：448 评论：0 收藏：0 [点我收藏+]

标签：

当我们求解某些问题时，由于这些问题要处理的数据相当多，或求解过程相当复杂，使得直接求解法在时间上相当长，或者根本无法直接求出。对于这类问题，我们往往先把它分解成几个子问题，找到求出这几个子问题的解法后，再找到合适的方法，把它们组合成求整个问题的解法。如果这些子问题还较大，难以解决，可以再把它们分成几个更小的子问题，以此类推，直至可以直接求出解为止。这就是分治策略的基本思想。

1、引例：

如果给你一个装有16枚硬币的袋子，其中有一枚是伪造的，并且那枚伪造硬币的重量和真硬币的重量不同。你能不能用最少的比较次数找出这个伪造的硬币?为了帮助你完成这一任务，将提供一台可用来比较两组硬币重量的仪器，利用这台仪器，可以知道两组硬币的重量是否相同。

常规的解决方法是先将这些硬币分成两枚一组，每一次只称一组硬币，如果运气好的话只要称1次就可以找到，最坏最多称8次才可以找出那枚硬币，这种直接寻找的方法存在着相当大的投机性，适用于硬币数量少的情况，在硬币数量多的情况下就成为一件费时费力又需要运气的事。

试着改变一下方法：如果我们将全部硬币分成两组，将原来设计的一次比较两枚硬币变为一次比较两组硬币，我们会发现通过一次比较后．完全可以舍弃全部是真币的一组硬币，选取与原有问题一致的另一半进行下一步的比较，这样问题的规模就明显缩小，而且每一次比较的规模都是成倍减少(如图4－1所示)。

技术分享

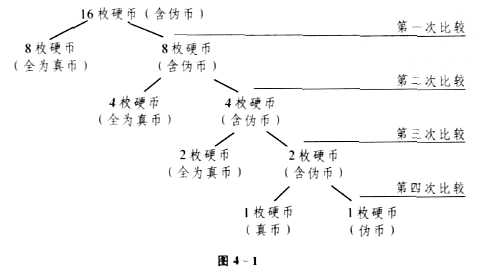
根据以上分析。我们可以得到以下的结论：

(I)参与比较的硬币数量越多，使用该方法来实现就越快．而且投机性大大减少；

(2)解决方法关键在于能将大问题分割成若干小问题；

(3)小问题与原有问题是完全类似的。

通常我们将这种大化小的设计策略称之为分治法．即“分而治之”的意思。

2、分治法的基本思想和解题的一般步骤：

分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。侧重点在于能各个击破。分治法在设计检索、分类算法或某些速算算法中很有效。最常用的分治法是二分法、归并法、快速分类法等。

分治法解题的一般步骤：

（1）分解，将要解决的问题划分成若干规模较小的同类问题；

（2）求解，当子问题划分得足够小时，用较简单的方法解决；

（3）合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。

1、解决算法实现的同时，需要估算算法实现所需时间。分治算法时间是这样确定的：　　　解决子问题所需的工作总量（由子问题的个数、解决每个子问题的工作量决定）；合并所有子问题所需的工作量

2、分治法是把任意大小问题尽可能地等分成两个子问题的递归算法

3、分治的具体过程大致如下：

　　 begin 　｛分治过程开始｝
　　　 if ①问题不可分 then ②返回问题解　
　　　　 else begin
　　　　　　　　 ③从原问题中划出含一半运算对象的子问题1；
　　　　　　　　 ④递归调用分治法过程，求出解1；
　　　　　　　　 ⑤从原问题中划出含另一半运算对象的子问题2；
　　　　　　　　 ⑥递归调用分治法过程，求出解2；
　　　　　　　　 ⑦将解1、解2组合成整修问题的解；　
　　　　　　　 end;
　　 end; {结束}

3、典型例题：

【例1】用递归算法和非递归算法实现二分查找即：有 n个已经从小到大排序好的数据，从键盘输入一个数m，用二分查找方法，判断它是否在这n 个数中。

 1 var a:array[1..20]of integer;
 2    n,i,m,x,y:integer;
 3 procedure  jc(x,y:integer);                    //递归过程
 4   var  k:integer;
 5   begin
 6     k:=(x+y)div 2;                            //取中间位置点
 7     if a[k]=m then writeln(‘the num in ‘,k);        //找到查找的数，输出结果
 8     if x>y then writeln(‘no find‘)                //找不到该数
 9      else begin
10            if a[k]<m then jc(k+1,y);            //在后半中查找
11            if a[k]>m then jc(x,k-1);            //在前半中查找
12          end;
13   end;
14 begin
15   readln(n);
16   x:=1;y:=n;
17   for i:=1 to n do readln(a[i]);            //输入排序好的数
18   readln(m);                            //输入要查找的数
19   jc(x,y);                                //递归查找
20 end.

递归法

 1 var a:array[1..20]of integer;
 2    n,i,m,x,y,k:integer;
 3 begin
 4   readln(n);
 5   x:=1;y:=n;
 6   for i:=1 to n do readln(a[i]);
 7   readln(m);
 8   repeat
 9     k:=(x+y)div 2;
10     if a[k]=m then begin writeln(‘the num in ‘,k);halt;end
11     else begin
12            if a[k]<m then x:=k+1;
13            if a[k]>m then y:=k-1;
14          end;
15   until x>y;
16   writeln(‘No find‘);
17 end.

非递归法

【例2】一元三次方程求解

有形如：ax³ +bx² +cx+d＝0这样的一个一元三次方程。给出该方程中各项的系数（a，b，c，d 均为实数），并约定该方程存在三个不同实根（根的范围在-100 至 100 之间），且根与根之差的绝对值≥1。要求由小到大依次在同一行输出这三个实根（根与根之间留有空格），并精确到小数点后 2 位。