C语言之广度优先算法

标签：

广度优先算法又称宽度优先搜索，是一种简便的图的搜索算法之一。搜索方式大致是这样的：

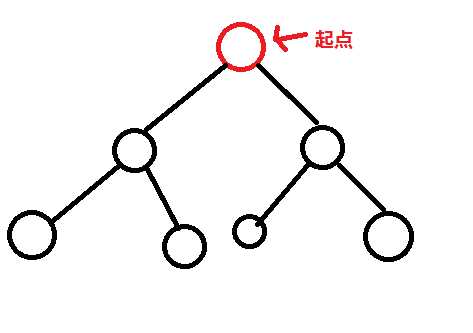
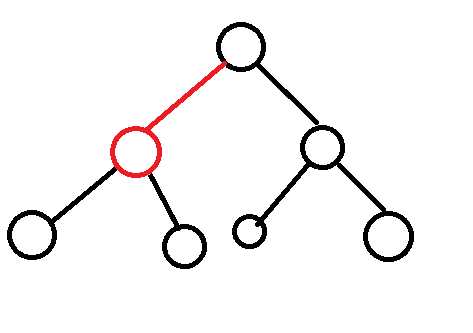
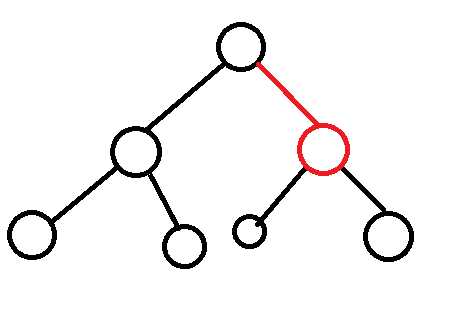
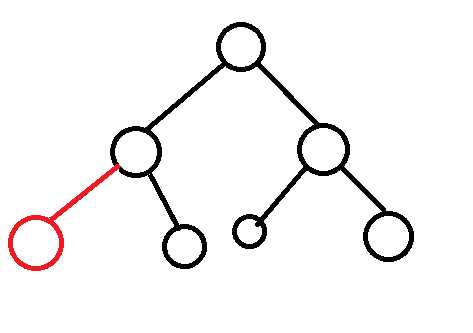
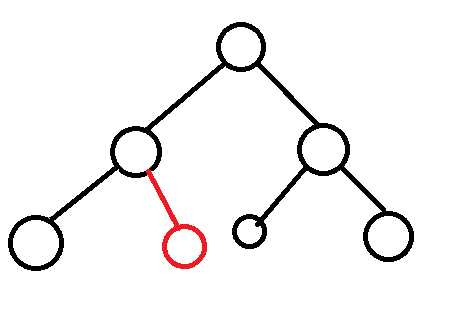
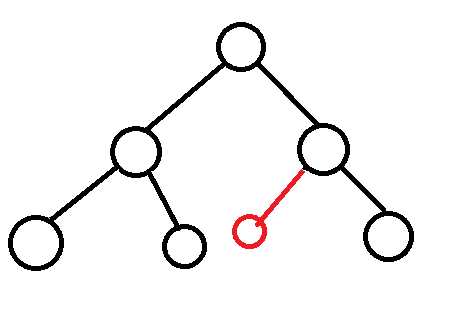
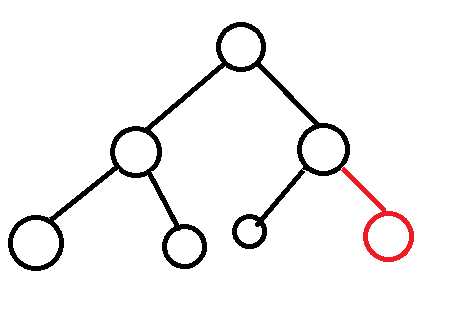
直到搜索到目标节点（节点就是那些圆球球，其中有一个或者多个是目标节点）或者搜完了整个图都没找到目标节点就停止搜索。

实现这个要是想用像深度优先算法那样函数套函数那样是难以实现的（至少我实现不了）。

像这样的：

求问从A到B的最短路径的节点数是多少？

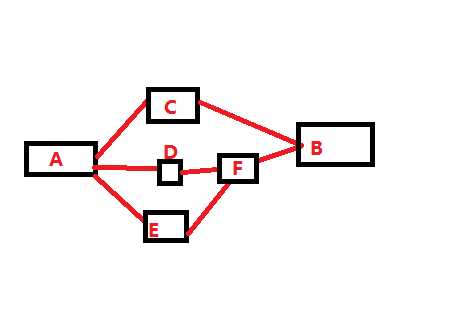
这道题很简单嘛，肯定是A-C-B啊，答案是3啊。那怎样用C语言实现呢？

深搜的话：一条路一条路读取，取节点数最小的，也可以，但是问题来了，当节点数特别多，图非常“辽阔”时，怎么办呢？

用广搜啦！

这里设A的标志为0（这样好些代码嘛），其他的以此类推，所以路径A-C-B就是0-2-1啦

根据路是不是相同的，我们可以创建一个布尔型二维数组way，way[w1][w2]=1代表从w1可以到达w2，=0时则代表不能,注意，因为我们是不会走回头路的，所以所有路都是单向的，比如c->b是可以的，但b->c是不可以的

_Bool way[6][6]={
{0,0,1,1,1,0},
{0,0,0,0,0,0},
{0,1,0,0,0,0},
{0,0,0,0,0,1},
{0,0,0,0,0,1},
{0,1,0,0,0,0},
};

创建一个step变量，初始值为0，储存列出了几层子节点，也就是目前所有路径的节点数

创建一个队列，比如叫que（其实就是个数组嘛）

简单讲下队列的概念：有队首(head)和队尾(tail)两个指针，分别指着队列的第一个元素与最后一个元素。队列只允许从队尾加入队伍，从队首退出队伍。

此时head=tail=0：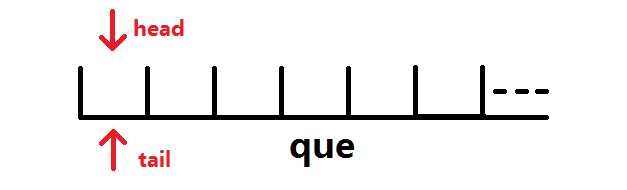

在队列que中加入A节点的标志0，步骤是将tail+=1并且que[tail]=0（如图所示）

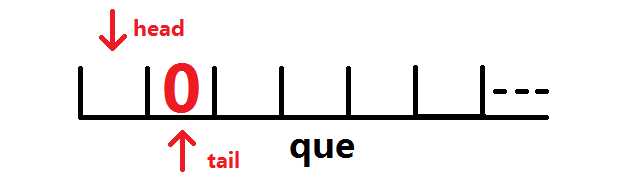
然后搜索A的子节点，例如这样：

循环(i=0;i<=5;i++)//因为共有6个节点

如果(way[que[head+1]][i]==1)把子节点加入队列；

加入队列的方法就是：

tail+=1;

que[tail]=子节点标志;

最后效果如图

当循环完毕以后呢，就等于把A的子节点全找出来了，列出了一整曾节点，step+1，删去第一个节点，head-=1，那样head指的就是A的子节点C(标志3)了如图

继续判断，搜索3的子节点，并且加入队列，再删去3，搜索4的子节点……直到最后tail指针指的是B(标志2)，则输出step，就是最短路径数。如果head=tail了，说明队列为空，而且没找到答案，所以就没有可以到达目标节点的路，输出什么的就随你了。

附上此题答案：

#include <stdio.h>

_Bool way[6][6]={
{0,0,1,1,1,0},
{0,0,0,0,0,0},
{0,1,0,0,0,0},
{0,0,0,0,0,1},
{0,0,0,0,0,1},
{0,1,0,0,0,0},
};

int main()
{
    int que[101],head=0,tail=0,i,step=1;
    tail++;
    que[tail]=0;
    do
    {
        step++;
        for(i=0;i<=5;i++)
        {
            if(way[que[head+1]][i]==1)
            {
                tail++;
                que[tail]=i;
                if(que[tail]==1)
                {
                    printf("%d",step);
                    return 0;
                }
            }
        }
        head++;
    }while(head!=tail);
    printf("foolish man,no answer!");
    return 0;
}

C语言之广度优先算法

标签：

原文地址：http://www.cnblogs.com/rjgcs/p/5198467.html