1、问题描述

　　谱聚类(Spectral Clustering, SC)是一种基于图论的聚类方法——将带权无向图划分为两个或两个以上的最优子图(sub-Graph)，使子图内部尽量相似，而子图间距离尽量距离较远，以达到常见的聚类的目的。

　　对于图的相关定义如下：

• 对于无向图G = (V,E)，V表示顶点集合，即样本集合，即一个顶点为一个样本；E表示边集合。
• 设样本数为n，即顶点数为n。
• 权重矩阵：W，为n*n的矩阵，其值w_i,j为各边的权值，表示顶点 i，j（样本）之间的相似性。对于任意w_i,j = w_j,i ，w_i,i=0，即对角线上元素为0。
• 通常情况下，相似性小于某一阈值的两个顶点不相连，否则连接两顶点的边的权值为两个样本的相似性度量函数的值。
• 定义n*n的矩阵：D，其第 i 行，第 i 列的元素（对角线上）元素为W第 i 行所有元素的和，即 i 顶点与其他所有顶点的相似性之和。

• 将图G分割为子图G₁,G₂，所要断开的边的权重之和为损失函数：

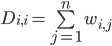
如下图给出一个六个样本所对应的图：此例中对应的损失函数为 w_{1,5 +} w_3,4 = 0.3。

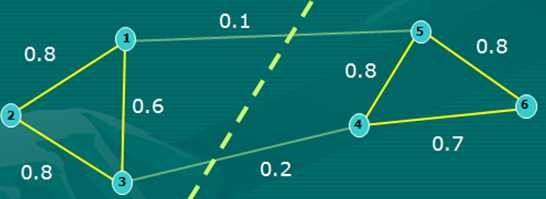
　　谱聚类的目的就是找到一个较好的划分准则，将整个样本空间形成的图分成为各个子图(sub-Graph)，一个子图即为一个类别。根据分割子图的准则，可以将其分为不同的谱聚类（Minimum Cut、Ratio Cut and Normalized Cut等）。

　　讲具体算法之前，回顾一些线性代数有关的结论，不清楚的可以查阅相关资料：

• Ax = λx ，则λ为A的特征值，x为对应λ的特征向量。
• 对于实对称矩阵A，其特征向量正交。即当i ≠ j时， <x_i^T,x_j> = 0（<,>表示内积）。
• 对于正定矩阵，其所有特征值都大于0；对于半正定矩阵，其所有特征值都大于等于0

2、问题转化

　　首先看看这个损失函数，对其进行如下变换：

1、定义q_i如下：

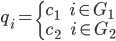
当顶点 i 属于子图G₁中时，q_i = c₁。顶点 i 属于子图G₂中时，q_i = c₂。

2、Cut(G₁,G₂)变形：

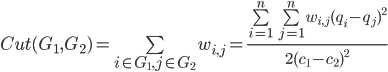
当且仅当i，j属于不同子图时，(q_i - q_j)²/(c₁ - c₂)² = 1，否则(q_i - q_j)²/(c₁ - c₂)² = 0。常数1/2：由每个 i 遍历一遍 j ，这样，被剪断的边的权值被计入了两次，所以除以2。

3、Cut(G₁,G₂)分子变形：

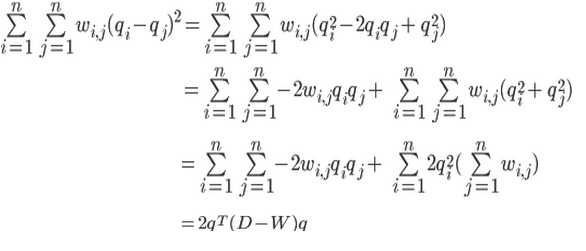
4、拉普拉斯矩阵 L = D - W，满足：

 

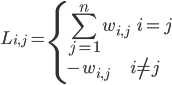
5、问题转化：

由第3步，等式首尾可知：

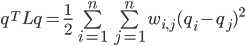
因此，总结上述推导，有下式：

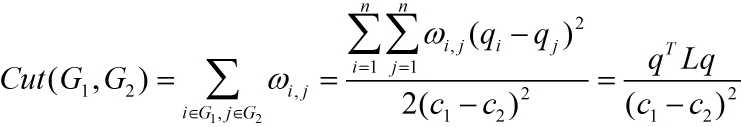
因为w_i,j ≥ 0，所以q^TLq对于任意的q ≠ 0，都有 q^TLq ≥ 0，所以L为半正定的矩阵，其L为实对称矩阵。有如下三条性质：

1. L所有特征值 ≥ 0 ，且特征值对应的特征向量正交。
2. L有一个等于0的特征值，其对应的特征向量为[1,1,...,1]^T，此值的具体意义，后文介绍。
3. 所有非零的特征向量与[1,1,...,1]^T的内积为0，即正交。

第一点在文章开头结论中以提及，不做详述，对于第2点，我们来好好看看这个L。对于文章最初的样本集，有如下矩阵，下图分别对应于W,D,L矩阵。

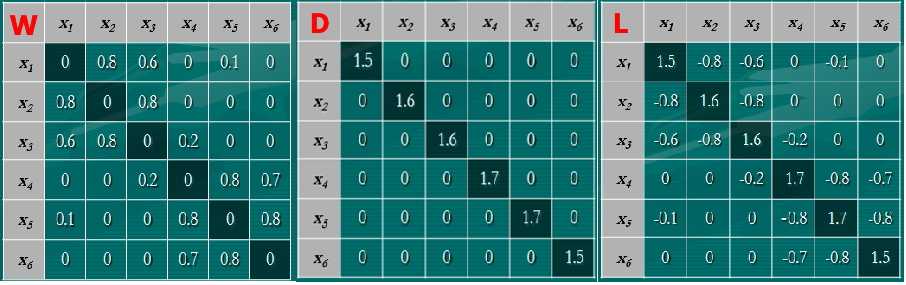
对于向量λ₀=[1,1,1,1,1,1]^T总能使得，L*λ₀ = 0 = 0*λ₀，所以0总是L的特征值，且0特征值对应的特征向量为[1,1,...,1]^T。第2点理解了，第3点也自然可以理解了。

　　因此，最终将最小化损失函数Cut(G₁,G₂)问题转化为最小化多项式q^TLq，只不过对应于不同的准则，其限制条件有所不同，可以利用瑞丽熵(Rayleigh quotient)的性质求解，接下来将逐一介绍。

3、划分准则

　　首先，来看看型如 q^TLq 的多项式的优化问题。在此之前，先看看Rayleigh quotient（具体见维基百科），此处只列出部分性质：

对于Rayleigh quotient定义如下：

• 对于一个给定的M，R(M,x)的最小值为λ_min（为M的最小特征值），当且仅当x = v_min（为对应的特征向量）时，同样的，R(M,x) ≤ λ_max，且R(M,v_max) = λ_max。

利用拉格朗日乘数法，可以求解多项式的 critical points（极值点）问题（具体过程参考Rayleigh quotient：Formulation using Lagrange multipliers）：

• 对于多项式 ，s.t.  求解极值。
• 加入拉格朗日乘数后，求导可得Mx = λx ，即x为M的特征向量时，R(M,x)取得极值，带入上式可得极值为R(M,x) = λ，即对应的特征值。

我们第二节最后的式子再强调一遍，以便后文阅读，此式记为公式(1)：

3.1、MINIMUM CUT 方法

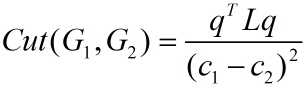
　　Minimum Cut 的目标函数即为公式(1)，对于c₁，c₂取任何数都不影响分类结果（当然不能相等，因为无法区分相等的东西，c₁为样本属于G1的标签，同理c₂为样本属于G2的标签，标签相等时，就无法区分），但是会影响求解过程：c₁，c₂ 影响瑞丽熵求的求解条件是否满足，即。为了方便求解，我们选择如下，

　　当c₁ = - c₂ = 1时，即q为：

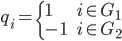
　　此时最小化公式(1)的求解变为： 

限制条件中，第一条，可以由向量q元素取值只能是1或-1；第二条，上文已提及，e为元素全为1的向量，e为L的最小特征向量，L的所有特征向量正交。

　　此问题求解方法在第3节和3.1之间已经提及，其最优分类方案q为L的最小特征值对应的特征向量，L的最小特征值0（即为目标函数最小值），对应的特征向量即为e。可以解释：可以找到一个使目标函数为0（所剪切边权重之和为0）的方案，为：所有样本属于G₁类（因为q此时对应的值全为1，对应i∈G₁），0个样本属于G₂类。这是始终存在的但毫无意义的分类。因此，将其排出（即第二限制条件的作用）。

　　综上，求解上述问题，只需求解L的第二小的特征值对应的特征向量，对特征向量进行聚类。此时问题的转变：将离散的问题的求解转为连续问题的求解（此处将问题松弛化了，使得NP-hard问题变为了P问题），最后再进行离散化。

• 连续问题：求解多项式q^TLq的最小值 =》 求L的特征值及其特征向量。
• 离散化：最初的q_i为：1属于G₁，-1属于G₂。最后求得的q并非为最初定义的 q_i 中的离散值，值的大小只作为一种指示。可以很容易的找到一个合理的阈值，分割最终的q，即 q_i > 0 属于G₁，q_i < 0 属于G₂。

　　问题：这样的目标函数忽略的孤立点的存在，如下图：

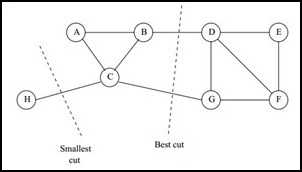
w_h,c < w_b,d + w_c,g 时，聚类结果为H为一类，其他所有点为一类。若对应于 0.3 < 0.2 + 0.2，将导致图中Smallest cut的结果，这样的分类显然是不合理的，我们更希望的是Best cut的结果。为了避免这样的想象，使得类别数量相对均衡，引入了Ratio Cut 方法。

3.2、RATIO CUT 方法

　　先看看Ratio Cut 的目标函数 公式(2)：

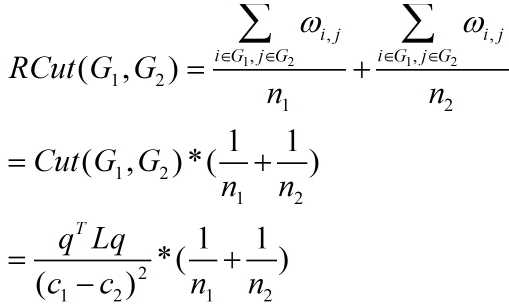
其中n₁为属于G₁中的顶点数，n₂同理。对应上图分析，若为图中Smallest cut，则RCut(G₁,G₂) = 0.3/1 + 0.3/7 = 0.34，为图中Best cut，则RCut(G₁,G₂) = (0.2+0.2)/4 + (0.2+0.2)/4 = 0.2，显然避免了这种情况，不仅考虑了剪断边的权值，还考虑了各类别中样本数量的均衡。

　　此时要转化为瑞丽问题，将q_i定义如下：

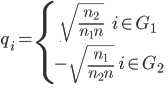
带入公式(2)为（别忘了n₁+n₂=n，n为常数）：

此时又问题以转化为瑞丽熵可求解的问题：

限制条件q^Tq：

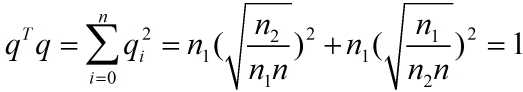
接下来的工作于3.1相同。

3.3、NORMALIZED CUT 方法

　　上述方法都没有考虑子图内部的权重系数。Normalized Cut加入了对子图内部的权重。目标函数如下公式(3)：

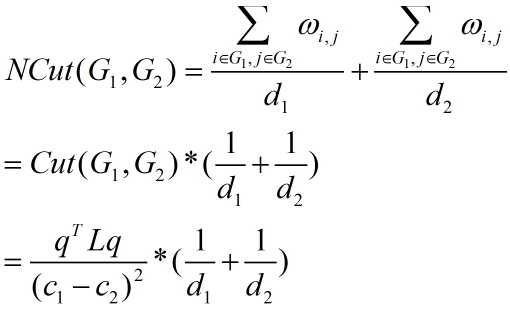
其中d₁为G₁内所有边权重之和加上Cut(G₁,G₂)，d₂为G₂内所有边权重之和加上Cut(G₁,G₂)，d = d₁ + d₂ - Cut(G₁,G₂)。如下图所示：(d₁=asso(A,A)+cut(A,B)，d₂=asso(B,B)+cut(A,B))

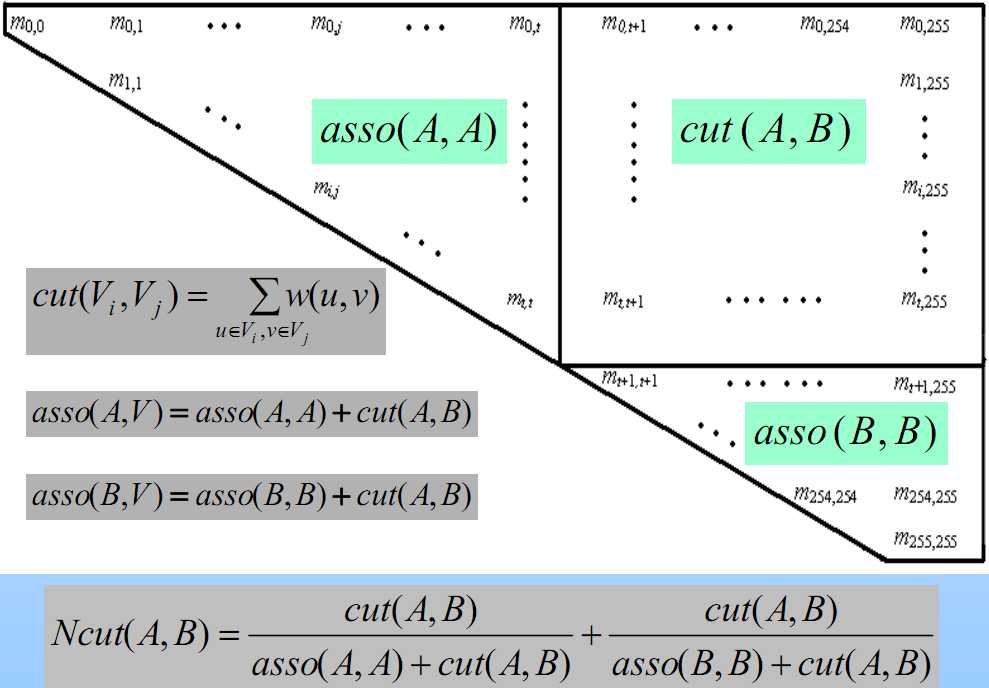
为了转化问题，将q_i定义如下：

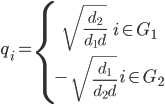
带入公式(3)为:

问题转化为（其实这是一个Generalization Rayleigh quotient模型）：

其中限制条件为：

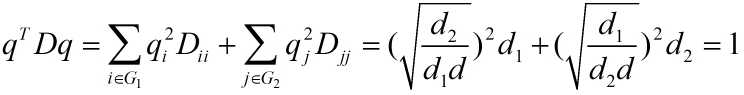
此处的求解，仍然是将目标函数加上第一个限制条件与拉格朗日乘数后求导，不同的限制条件中多了一个D矩阵，求导后与之前的结果（Mx = λx）稍有不同。

step1：

step2：

step3：

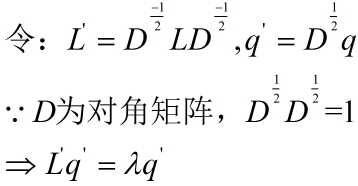
step4：

　　此时，求解归一化的拉普拉斯矩阵(Normalized Laplacian，对角线元素全为1) L’ = D^-1/2 L D^-1/2 的特征值及其对应的特征向量即可。 因为 L 和 L’ 的特征值是相同的，特征向量的关系为 q’ = D^1/2q，所以可以求L’的特征值对应的特征向量，最后在乘以D^-1/2即可求得q。(以上提及的特征向量皆为第二小特征值对应的特征向量)

4、总结

　　以上提及皆为聚类为两类的情况，当使用谱聚类进行K聚类是，即可选取除特征值为0以外的，前K小的特征值对应的特征向量(大小为n*1），组成一个特征矩阵（以特征向量为列组成的大小为n*k的矩阵）。矩阵中，行向量即为该行对应样本的特征空间表示。 最后利用k-means等其它聚类算法进行聚类。

　　按照划分准则的不同，可以将谱聚类分为两种：Unnormalized Spectral Clustering & Normalized Spectral Clustering，区别在于Laplacian矩阵是否是规范化，Ratio Cut & Minimum Cut 皆为 Unnormalized。

 

1、Unnormalized Spectral Clustering算法

　　算法输入：样本相似矩阵S和要聚类的类别数K。

• 根据矩阵S建立权重矩阵W、三角矩阵D；
• 建立Laplacian矩阵L；
• 求矩阵L的（除0外）前K小个特征值及其对应的特征向量；
• 以这K组特征向量组成新的矩阵，其行数为样本数，列数为K，这里就是做了降维操作，从N维降到K维；
• 使用k-means等其它聚类算法进行聚类，得到K个Cluster。

 

2、Normalized Spectral Clustering算法

　　算法输入：样本相似矩阵S和要聚类的类别数K。

• 根据矩阵S建立权重矩阵W、三角矩阵D；
• 建立Laplacian矩阵L以及L’ = D^-1/2 L D^-1/2 ；
• 求矩阵L’的（除0外）前K小个特征值及其对应的特征向量；
• 利用q’ = D^1/2q求得对应的K个q；（q不是L的特征向量）
• 以这K组特征向量组成新的矩阵，其行数为样本数N，列数为K；
• 使用k-means等其它聚类算法进行聚类，得到K个Cluster。

 

Spectral Clustering的各个阶段为：

• 选择合适的相似性函数计算相似度矩阵来建立权重矩阵W；如：

 

• 计算矩阵的特征值及其特征向量，比如可以用Lanczos迭代算法；
• 如何选择K，可以采用启发式方法，比如，发现第1到m的特征值都挺小的，到了m+1突然变成较大的数，那么就可以选择K=m；
• 使用k-means算法聚类，当然它不是唯一选择；
• Normalized Spectral Clustering在让Cluster间相似度最小而Cluster内部相似度最大方面表现要更好，所以首选这类方法。

 

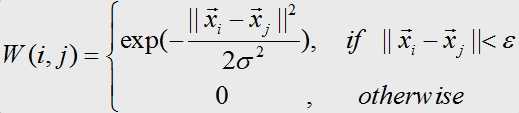
Spectral Clustering的性能：

• 比传统k-means要好，Spectral Clustering 是在用特征向量的元素来表示原来的数据，并在这种“更好的表示形式”上进行 K-means，这种“更好的表示形式”是用 Laplacian Eigenmap 进行降维的后的结果 。
• 计算复杂度比 k-means 要小。这个在高维数据上表现尤为明显。例如文本数据，通常排列起来是维度非常高（比如，几千或者几万）的稀疏矩阵，对稀疏矩阵求特征值和特征向量有很高效的办法，得到的结果是一些 k 维的向量（通常 k 不会很大），在这些低维的数据上做 k-means 运算量非常小。但是对于原始数据直接做 k-means的话，虽然最初的数据是稀疏矩阵，但是 k-means 中有一个求 Centroid 的运算，就是求一个平均值：许多稀疏的向量的平均值求出来并不一定还是稀疏向量，事实上，在文本数据里，很多情况下求出来的 Centroid 向量是非常稠密，这时再计算向量之间的距离的时候，运算量就变得非常大，直接导致普通的 k-means 巨慢无比，而 Spectral Clustering 等工序更多的算法则迅速得多的结果。