标签:
作者:jasonkent27
转载请注明出处:www.cnblogs.com/jasonkent27
小明和小天现在住在海口(C1),他们俩计划暑假到三亚(C4)玩一趟,在海口和三亚之间有许多中间城市(文昌,临高,乐东,万宁...)图中的边上的数字是他们到达该城市必须的花费,现在需要你帮他们俩找出一条从海口到三亚的最省钱的路径出来。
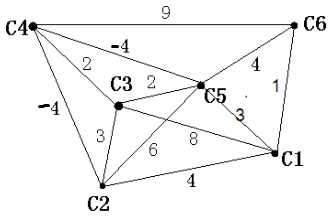
等等,图中的边的weight怎么会有负的呢?你暂且可以这么理解吧。图中的边上的weight可以当作他们旅途中必须的花费,但是他们俩在去三亚图中把钱花光了(真是败家)不得不通过搬砖赚钱,通过搬砖赚的钱不仅抵掉他们应该的花费,而且还赚了点小钱(但是他们不能一直搬砖啊,不然他们早就累挂了,哪里还能去玩)。
对边进行松弛操作的过程如下:
void relax(int u, int v, int w)
{
if ( dist[v]> dist[u] + w )
dist[v] = dist[u] + w ;
}
void init(int v0)
{
for (int i = 1 ; i <= n ; i ++)
dist[i] = infinity ;
dist[v0] = 0 ;
}
最短路径具有最优子结构性质
路径松弛性质
上界性质
收敛性质
最短路径一定是简单路径
这几条性质是后面最短路算法的数学依据,如果想要彻底理解最短路的算法,有必要对其深究
即最短路径的子路径也是最短路径
简单证明:如果最短路径P的子路径不是最短路径,则可以找到一条更短的路径使得P更短,这与P是最短路径不符.
如果P=<v0,v1, ..., vk>是从源点s=v0到vk的一条最短路径,并且我们对P中的边所进行松弛的次序为(v0,v1),(v1,v2), ..., (vk-1,vk),则dist[vk] = delta(s,vk),why?
我们可以用归纳法进行证明:
1.当v = s,时 dist[v] = delta(s,s) = 0,显然成立
2.假设当v = vk-1时,dist[v] = delta(s,v) = delta(s,vk-1)成立,如果我们能推出dist[vk] = delta(s,vk),则命题成立。
因为
dist[vk] >= dist[vk-1] + w(vk-1,vk)
= delta(s,vk-1) + w(vk-1,vk)
= delta(s,vk) (收敛性质)
则原命题也是成立的.
对于所有节点v, 有dist[v] >= delta(s,v),且当dist[v]=delta(s,v)之后,dist[v]的值不会再变化.
此性质亦可用归纳法证明:
1.进行init(v0)后,显然满足对所有v, dist[v] >= delta(s,v)
2.假设松弛前,对所有v, dist[v] >= delta(s,v),我们只要再证明松弛后,
假设s-->u-->v为s-->v的一条最短路径,在某个时刻dist[u] = delta(s,u),则在边(u,v)松弛之后有dist[v] = delta(s,v)
证明:在边松弛之后应该有
dist[v] <= dist[u] + w(u,v)
= delta(s,u) + w(u,v)
= delta(s,v) (最短路最优子结构性质)
而根据上界性质,dist[v] >= delta(s,v),因此dist[v] = delta(s,v)
why? 为何最短路径一定是简单路径(即无环)?
理由如下:假设最短路径有环,则有以下三种情况:
1.正环,然后去掉正环会使最短路径更短,不符合
2.零环,零环对最短路径没有影响,可以去掉
3.负环,如果存在负环,则不会有最短路径,因为我循环一圈都可以是u到v的路径更短.
Bellman-Ford算法通过不断构建以源点为根的最短路径树,不断扩展.
简单来说,先找出,扩展一条边,源点到达其他节点的最短路径,再找出扩展两条边,源点到达其他节点的最短路径,以此类推,找到通过扩展n-1条边,源点到达其他节点的最短路径,算法完毕。因为我们知道最短路径是简单路径,因此它无环,所以它最多有n-1条边.算法思路类似bfs.其正确性可以用路径松弛性质证明.
示意图如下(图片来自算法导论):
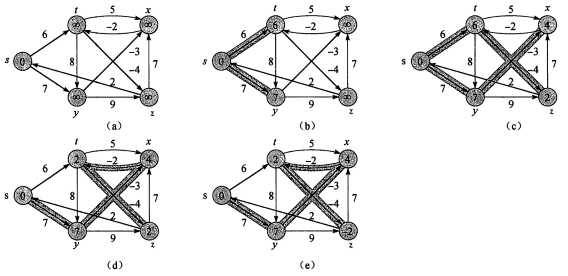
先是从s扩展一条边,可以达到t,y(图b),此时我们知道,在只扩展一条边的前提下,s到t,y的最短路径分别是dist[t],dist[y],然后再通过t,y继续扩展边(图c),这时我们有,在只扩展两条边的前提下,s到x,z的最短路径分别是dist[x],dist[z]。当然有个前提假设是s到其他节点都有最短路径.看看整个过程有没有觉得特别像通过bfs找最短路的过程.
bool Bellman_Ford(int v0)
{
init(v0) ;
for(int i=1 ; i<=n-1 ; i++)
for(int j=1 ; j<=m ; j++)
relax(edge[j].u,edge[j].v,edge[j].w);
for(int i=1 ; i<=m ; i++)
{
int u = edge[i].u ;
int v = edge[i].v ;
int w = edge[i].w ;
if (dist[v] > dist[u] + w)
return false ;
}
return false ;
}
我们可以轻松知道Bellman-Ford算法的时间复杂度是O(nm)的,我们再想想,是不是每次都需要对M条边进行松弛操作的,显然没必要,而且我们发现如果在某次循环中,发现对M条不管怎么relax,dist数组都不会变化,那么算法就可以停止了(上界性质).SPFA算法就是在这2点上对Bellman-Ford算法进行优化的。SPFA算法时间复杂度为O(qm),其中q远远小于n.在实战中有不错的效率,不过可以造出让SPFA效率低的数据。因此在如果题目没有负边,个人倾向于基于优先队列实现的Dijkstra算法.
void SPFA(int v0)
{
queue<int> q ;
init(v0) ;
q.push(v0) ;
inq[v0] = true ;
while (!q.empty())
{
int u = q.front(); q.pop();
inq[u] = false ;
for (int i=1 ; i<=n ; i++) //此处若用邻接表则更快
if (g[u][i] !=0 && dist[i] > dist[u]+g[u][i])
{
dist[i] = dist[u]+g[u][i] ;
if (inq[i] == false)
{
q.push(i);
inq[i] = true ;
}
}
}
}
维护集合U,用来保存那些已经计算过最短路的节点即dist[v] = delta(s,v)的节点,不断增大集合U,直到U包含图中所有节点.
1.选出V-U集合中最小的dist[x]
2.把x加入到U中
3.用dist[x]去更新所有V-U集合的所有节点dist值,(U集合中的dist值已经达到下限delta(s,v)了,没必要再更新)
void Dijkstra(int v0)
{
init(v0) ;
for (int i=1 ; i<=n-1 ; i++)
{
min = infinity ;
for (int j=1 ; j<=n ; j++)
if (!inq[j] && dist[j]<min)
{
min = dist[j] ;
k = j ;
}
inq[k] = true ;
for(int j = 1 ; j<=n ; j++)
if (!inq[j] && dist[j]>dist[k]+g[k][j])
dist[j]>dist[k]+g[k][j] ;
}
}
算法执行过程
1.首先从V-U集合中选出dist值最小的节点s(图a),然后拿它去更新其他节点(图b)
2.把节点s加入到U集合中
3.不断重复此过程,直到U=V位置(图c,d,e,f)
要证明算法的正确性,我们只需要证明当节点u加入到集合U时,有dist[u]=delta(s,u)即可.
用反证法:假设u是第一个加入到集合U时,满足dist[u] != delta(s,u)的节点.
由于节点s是第一个加入到集合U的,并且有dist[s] = delta(s,s)=0,因此节点u与节点s必然不同,因此一定存在某条从节点s到节点u的路径,否则dist[u] = infinity,是不会被选入集合U中的.因为至少存在一条从s到u的路径,因此也存在一条从s到u的最短路径.
考虑这样一条路径s---->x-->y---->u,其中,s,x在集合U中,y,u在V-U集合中,
因为x在u加入之前就已经加入到U集合中了,因此有dist(x) = delta(s,x),而x是y前驱,对边(x,y) relax后,有dist[y] = > delta(s,y)(收敛性质)
因为y是u的前驱,且边权值非负,因此有dist[y] = delta(s,y) <=delta(s,u)<=dist[u].
另外,算法选择u节点放进集合U的前提是u是所有V-U集合中dist值最小的,因此有dist[y] >= dist[u].
综上,有dist[y] = dist[u] = delta(s,u).这与假设dist[u] != delta(s,u)不符.因此原命题是成立的.
floyd算法用来求图中任意点对之间的最短路径.将floyd算法之前我们先来看看另外一个用O(V^4)来解决图中任意点对之间最短路径的算法。
通过前面的知识我们知道,任意两个节点之间的最短路径无非就两种情况
1.i, j 直接相连
2.i, j 间接相连
若是直接相连,则delta(i,j) = g[i][j] ;
若间接相连,设其路径为i------>k-->j(k为j前驱),则有
delta(i,j) = delta(i,k) + g[k][j] (收敛性质)
我们定义dist[m][i][j] 表示最多可以通过m条边,节点i,j之间的最短距离,则有dist[m][i][j] = min(dist[m-1][i][j],dist[m-1][i][k] + g[k][j]) = min(dist[m-1][i][k] + g[k][j]),其中1<=k<=V,dist[0][i][j] = g[i][j].
伪代码如下
void Shortest_Path_Pair()
{
for (int u = 1 ; u<=n-1 ; u++) //因为最短路最多只有n-1条边
for (int i=1 ; i<=n ; i++)
for (int j = 1 ; j<=n ;j++ )
for (int k=1 ; k<=n ; k++)
//当然此处dist[u][i][j]可以降维成dist[i][j].
dist[u][i][j] = min(dist[u-1][i][j],dist[u-1][i][k]+g[k][j]) ;
}
OK,热身结束!我们来看看floyd算法,上面算法类似于Bellman_Ford,他们都是从路径中边的性质来考虑的。现在我们换个思路,从中间节点开始考虑,考虑节点i,j间最短路径p与中间节点均取自{1,2,...,k-1}的关系.
如果节点k不是路径p上的中间节点,则节点i,j路径上的中间节点均取自{1,2,...,k-1}的最短路径也是节点i,j路径上的中间节点均取自{1,2,...,k}的最短路径
如果节点k是路径p上的中间节点,则我们可以把路径分解成i--->k--->j,对于路径i-->k,其路径上的节点也肯定全部来自{1,2,...,k-1},因为k不是路径i-->k的中间节点,路径k-->j同理,看下图:
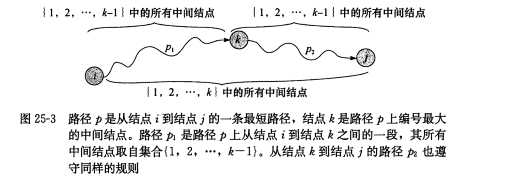
因此我们可以定义d[k][i][j] 表示i,j之间节点编号最大为k时的最短距离,我们有
d[k][i][j] = min(d[k-1][i][j], d[k-1][i][k]+d[k-1][k][j])
当然d[k][i][j]也是可以降维成d[i][j].其中1<=k<=V,d[0][i][j] = g[i][j].
void Floyd()
{
for (int k = 1 ; i<=n ; k++)
for (int i = 1; i<=n ; i++)
for (int j = 1 ; j<=n ; j++)
if (d[i][j] > d[j][k] + d[k][j])
d[i][j] = d[j][k] + d[k][j] ;
}
本文对求最短路径的几种基本算法做了简单的讲解,力求做到简单,易懂,更严格的算法正确性的证明可以查阅参考书目,文中有任何错误之处请指出,我会尽快改正.另外有何问题,欢迎留言讨论.
《算法导论》 第三版
标签:
原文地址:http://www.cnblogs.com/jasonkent27/p/5263206.html