标签:

R是用于统计分析、绘图的语言和操作环境。R是属于GNU系统的一个自由、免费、源代码开放的软件,它是一个用于统计计算和统计制图的优秀工具。
特点介绍
•主要用于统计分析、绘图、数据挖掘
•R内置多种统计学及数字分析功能。R的功能也可以通过安装包(Packages,用户撰写的功能)增强。
•因为S的血缘,R比其他统计学或数学专用的编程语言有更强的面向对象(面向对象程序设计)功能
官网:http://cran.r-project.org/
其他介绍
•R的另一强项是绘图功能,制图具有印刷的素质,也可加入数学符号。
•虽然R主要用于统计分析或者开发统计相关的软件,但也有人用作矩阵计算。其分析速度可媲美专用于矩阵计算的自由软件GNU Octave和商业软件MATLAB。
•SPSS-另一种统计分析软件
•SAS系统-另一种统计分析软件
安装
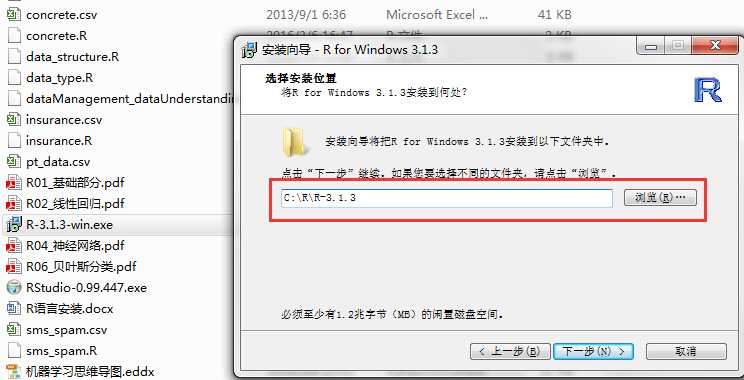
•R官网下载3.1.3
在安装R语言环境的时候,安装目录最好是不要包含空格、特殊字符、中文字符等,否则在安装Rstudio的时候,可能找不到R运行环境的地址;
•IDE开发环境使用Rstudio
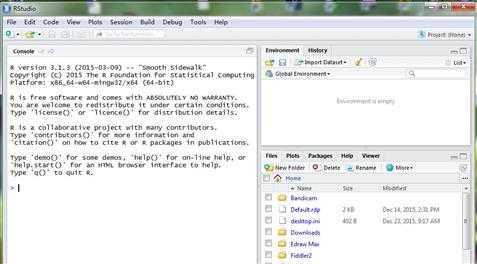
Rstudio下载地址:https://www.rstudio.com/products/rstudio/download/ 安装完成以后就是下面的样子,非常轻量级的工具:
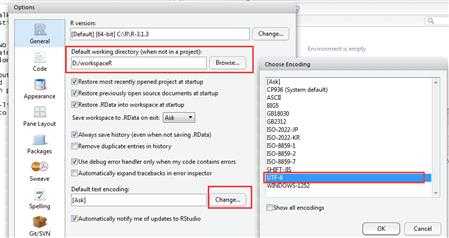
配置Rstudio的空作空间和默认编码方式,Tool-》Global Options...
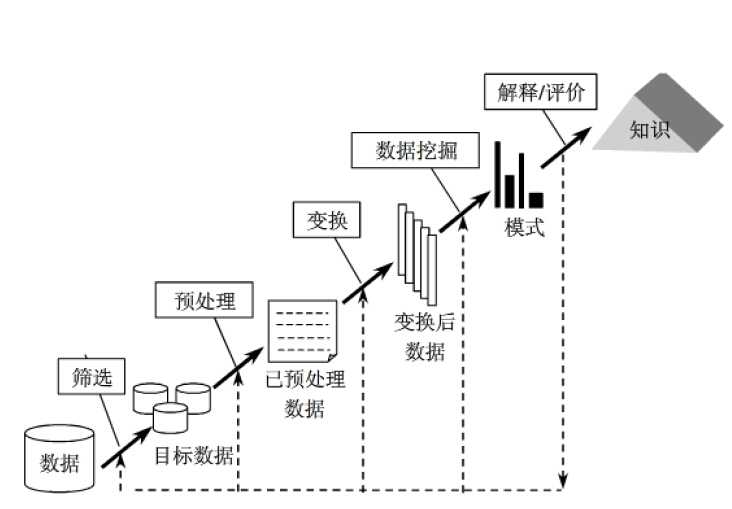
数据的管理和理解
•学完本章后,你将理解:
–基本的R数据结构以及如何使用这些数据结构来存储和提取数据
–如何把不同来源格式的数据导入R
–理解并可视化复杂数据的常用方法
数据结构
•向量
•R的基本数据结构式向量。向量存储一组有序的值,称为元素。
•一个向量可以包含任意数量的元素。然而,所有的元素必须是一样的类型,比如,一个向量不能同时包含数字和文本。
•integer numeric character logical NULL NA
•combine function
•R中的向量有固有的顺序,所以其数据能通过计算向量中各元素的序号来访问,序号是从1开始
•因子
•因子是向量的一个特例,它单独用来标识名义属性
•为什么不用character字符型向量呢?
•把字符型向量转换成因子,只需要应用factor()函数
•列表
•一种特殊类型的向量--列表,它用来存储一组有序的值
•列表允许收集不同类型的值
•用列表构建”对象”进行访问
•数组
•数据框
•机器学习中使用的最重要的R数据结构就是数据框,因为它既有行数据又有列数据,所以它是一个与电子表格或数据库相类似的结构
•新的参数stringAsFactors = FALSE
•提取其中的整个向量数据,就如列表提取一个元素那么简单,通过名字
•数据框是二维的,格式为“[rows, columns]”也可以提取数据
•矩阵
探索数据
•str()
•summary()
•table()
•plot()
数据管理
•保存和加载R数据结构
–save(x,y,z, file="mydata.RData")
–load("mydata.RData")
•用CSV文件导入和保存数据
–pt_data <-read.csv("pt_data.csv", stringsAsFactors=FALSE)
–pt_data <-read.csv("pt_data.csv", stringsAsFactors=FALSE, header=FALSE)
–write.csv(pt_data, file="pt_data2.csv")
•从SQL数据库导入数据
–RODBC
# R语言通过ODBC链接MYSQL数据库
mydb <- odbcConnect("localhost", uid="root", pwd="123123")
sqlTables(mydb)
students <- sqlQuery(mydb,"select * from Student")
students[1,2]
temp <- sqlFetch(mydb,"Student",rownames = "id")
odbcClose(mydb)
下面是交互式使用R的几个例子
例一:
> help.start() #启动在线帮助,会打开浏览器。 > x <- rnorm(50); y <- rnorm(x) #产生两个随机向量x和y > plot(x,y) #使用x,y画二维散点图, 会打开一个图形窗口 > ls() #查看当前工作空间里面的 R 对象 > rm(x,y) #清除x,y对象 >x <- 1:20 # 相当于x=(1,2,…,20)
例二:
x <- 1:20#等价于 x = (1, 2, ..., 20)。 w <- 1 + sqrt(x)/2#标准差的`权重‘向量。 dummy <- data.frame(xx=x, y= x + rnorm(x)*w)#创建一个由x 和 y构成的双列数据框 dummy #查看dummy对象中的数据。 fm <- lm(y ~ x, data=dummy)#拟合 y 对 x 的简单线性回归 summary(fm)#查看分析结果。 fm1 <- lm(y ~ x, data=dummy, weight=1/w^2)#加权回归 summary(fm1)#查看分析结果。 attach(dummy)#让数据框中的列项可以像一般的变量那样使用。 lrf <- lowess(x, y)#做一个非参局部回归。 plot(x, y)#标准散点图。 lines(x, lrf$y)#增加局部回归曲线。 abline(0, 1, lty=3)#真正的回归曲线:(截距 0,斜率 1)。 abline(coef(fm))#无权重回归曲线。 abline(coef(fm1), col = "red")#加权回归曲线。 detach()#将数据框从搜索路径中去除。 plot(fitted(fm), resid(fm), xlab="Fitted values", ylab="Residuals", main="Residuals vs Fitted")一个检验异方差性(heteroscedasticity)的标准回归诊断图。 qqnorm(resid(fm), main="Residuals Rankit Plot")#用正态分值图检验数据的偏度(skewness),峰度(kurtosis)和异常值(outlier)。 rm(fm, fm1, lrf, x, dummy)#再次清空。
例三: Michaelson 和 Morley 测量光速的经典实验
filepath <- system.file("data", "morley.tab" , package="datasets")#从对象 morley 中得到实验数据的文件路径
filepath#查看文件路径
file.show(filepath)#查看文件内容
mm <- read.table(filepath)#以数据框的形式读取数据
mm$Expt <- factor(mm$Expt)
mm$Run <- factor(mm$Run)#将 Expt 和 Run 改为因子。
attach(mm)#让数据在位置 3 (默认) 可见(即可以直接访问)。
plot(Expt, Speed, main="Speed of Light Data", xlab="Experiment No.")#用简单的盒状图比较五次实验。
fm <- aov(Speed ~ Run + Expt, data=mm)#分析随机区组,`runs‘ 和 `experiments‘ 作为因子。
summary(fm)
fm0 <- update(fm, . ~ . - Run)
anova(fm0, fm)#拟合忽略 `runs‘ 的子模型,并且对模型更改前后进行方差分析。
detach()
rm(fm, fm0)#在进行下面工作前,清空数据。
#下面是等高线和影像显示的示例
x <- seq(-pi, pi, len=50)#x 是一个在区间 [-pi\, pi] 内等间距的50个元素的向量
y <- x
f <- outer(x, y, function(x, y) cos(y)/(1 + x^2))#f 是一个方阵,行列分别被 x 和 y 索引,对应的值是函数 cos(y)/(1 + x^2) 的结果。
oldpar <- par(no.readonly = TRUE)
par(pty="s")#保存图形参数,设定图形区域为“正方形”。
contour(x, y, f)
contour(x, y, f, nlevels=15, add=TRUE)#绘制 f 的等高线;增加一些曲线显示细节。
fa <- (f-t(f))/2#fa 是 f 的“非对称部分”(t() 是转置函数)。
contour(x, y, fa, nlevels=15)#画等高线
par(oldpar)# 恢复原始的图形参数
image(x, y, f)
image(x, y, fa)#绘制一些高密度的影像显示
objects();
rm(x, y, f, fa)#在继续下一步前,清空数据。
th <- seq(-pi, pi, len=100)
z <- exp(1i*th)#1i 表示复数 i
par(pty="s")
plot(z, type="l")#图形参数是复数时,表示虚部对实部画图。这可能是一个圆。
w <- rnorm(100) + rnorm(100)*1i#假定我们想在这个圆里面随机抽样。一种方法将让复数的虚部和实部值是标准正态随机数 ...
w <- ifelse(Mod(w) > 1, 1/w, w)#将圆外的点映射成它们的倒数。
plot(w, xlim=c(-1,1), ylim=c(-1,1), pch="+",xlab="x", ylab="y")
lines(z)#所有的点都在圆中,但分布不是均匀的。
#下面采用均匀分布。现在圆盘中的点看上去均匀多了。
w <- sqrt(runif(100))*exp(2*pi*runif(100)*1i)
plot(w, xlim=c(-1,1), ylim=c(-1,1), pch="+", xlab="x", ylab="y")
lines(z)
rm(th, w, z)#再次清空。
q()#离开 R 程序
例子转自:http://developer.51cto.com/art/201305/393121.htm
标签:
原文地址:http://www.cnblogs.com/raphael5200/p/5264487.html